 ????????????????? ???? ? ?????? ????????? ? ????? ???????
????????????????? ???? ? ?????? ????????? ? ????? ???????
????
—
?????????????? ??????????
???????? ??????? ????? ???????, ??????? ??????? ???????? ??????? ???????. ???? ??? ?????????????? ?????? ???? ???????????? ???? ???????? — ????????? ????? ????????, ??????????? ??????????
??????
, ? ????????? ?? ?????? ??????, ??????????? ?????????? ?????. ??????? ????????? ????? ???? ???? ????????? ????????? ??????.
????? ??????? ??????? ?????????? ? ??????????? ????? ? ???????. ??? ???????????? ? ?
???????????? ??????
(?????? ? ?????) ? ?
?????????? ??????
(????????, ??????????), ?? ?????????? ????????? ?????????? ?????? ???????? ? ??????????? ? ??????? ???????????.
? ???????? ??????????? ??????? ?? ????? ????? ???????? ????? ????????? ???????????? ????????????, ??????? ???????????? ??????, ??? ????????? ????? ???????? ??????, ? ??????? — ?????, ??????????? ???? ???????. ?????? ????????? ? ?????????? ????? ???????? ??????: ?????, ????? ? ????? ???????? ?????????, ? ????? ?????????? ??????????? ?????? ? ????? ? ????? ? ?????
. ????????
?????????
????????????
??????????????? ??????
, ? ??????? ?????? — ??????? ?????, ? ??????????? — ???? (
???????????? ?????
).
????? ???????? ???????? ???????? ????????
?????? ??????
.
???????????
???????????? ??????? ??????? ???????? ??????? ???????? ??????? ?????????????, ??????? ?????????? ????? ????????? ?????. ?????????? ??????????? ?????? ? ??????????, ??????????? ??????? ???????, ????????
??????? ????
.
??????? ????
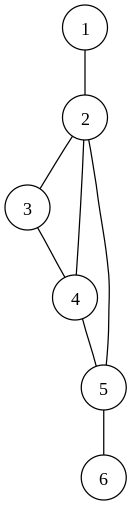
 ?????? ????????? ?????????????????? ?????
?????? ????????? ?????????????????? ?????
???????????.
??????? ????
 ???? ???????????? ???? ???????? – ????????? ?????????
???? ???????????? ???? ???????? – ????????? ?????????
 ? ?????????
? ?????????
 ??????????????? ??? ????????? ????????? ?????????
??????????????? ??? ????????? ????????? ?????????
 . ?????????
. ?????????
 ??????????
?????????? ??????
, ?????????
??????????
?????????? ??????
, ?????????
 ??????????
?????????? ?????
??????????
?????????? ?????
-
 ,
,
?? ???? ?????????
 ??????? ?? 2-?????????? ??????????? ?????????
??????? ?? 2-?????????? ??????????? ?????????
 .
.
????????????? ???????
?????? ?????? ?? ???????? ??????????? ?????????????. ??????? ? ????????? ??????????? ????? ?????????????? ???????, ???????? ?? ??????????? ????.
-
??????? (????, ?????)
(
????.
vertex, node, point) ?????
 ???? ??????? ????????? ??????
???? ??????? ????????? ??????
 ;
;
-
????? (?????)
(
????.
edge, line) ?????
 ???? ??????? ????????? ?????
???? ??????? ????????? ?????
 , ???
, ???
 , ???
, ???
 ;
;
-
??????????
?????
 ?????????? ??? ???????
?????????? ??? ???????
 ? ?????
? ?????
 ?????;
?????;
-
???????
(
????.
order) ?????
 ???? ???????????? ????? ????????? ??????
???? ???????????? ????? ????????? ??????
 ???, ??????? ???????, ?????????? ??????;
???, ??????? ???????, ?????????? ??????;
-
??????
(
????.
size) ?????
 ???? ???????????? ????? ????????? ?????
???? ???????????? ????? ????????? ?????
 ???, ??????? ???????, ?????????? ?????;
???, ??????? ???????, ?????????? ?????;
-
???????
 ??????????
(
????.
incident) ?????
??????????
(
????.
incident) ?????
 , ????
, ????
 ; ????? ??? ???????, ???
; ????? ??? ???????, ???
 ???? ????? ???
???? ????? ???
 ;
;
-
???????? ??????? (?????)
(
????.
endvertices, ends) ???? ??? ???????, ??????????? ?????. ?????
?????????
(
????.
joins) ???? ???????? ???????;
-
???????? (???????) ???????
(
????.
neighbours, adjacent) ???? ????? ???????
 ?
?
 ???
???
 ???, ???????, ??????? ??? ??????? ???????? ????????? ??? ?????? ?????;
???, ???????, ??????? ??? ??????? ???????? ????????? ??? ?????? ?????;
-
??????? ?????
(
????.
adjacent edges) ??? ?????, ??????????? ????? ??????? ???
 ?
?
 - ???????;
- ???????;
-
??????? (???????????) ???????
(
????.
degree, valency)
 ???? ?????????? ??????????? ?? ?????.
???? ?????????? ??????????? ?? ?????.
-
????????????? ????????
(
????.
isolated) ?????????? ??????? ?? ????????
 , ?? ???? ?? ???????? ?????? ?? ??? ?????? ?????;
, ?? ???? ?? ???????? ?????? ?? ??? ?????? ?????;
-
??????? ???????? (??????)
(
????.
leaf) ?????????? ??????? ?? ????????
 , ?? ???? ??????? ???????? ?????? ????? ?????? ?????.
, ?? ???? ??????? ???????? ?????? ????? ?????? ?????.
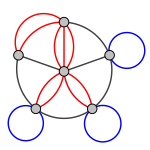
?????? ???? ??????????
??????????
: ??????? – ???????, ????? – ???????.
??????????
??????????
 ???? ???????????? ???? ???????? – ????????? ?????????
???? ???????????? ???? ???????? – ????????? ?????????
 ? ?????????
? ?????????
 ??????????????? ??? ????????? ?????????
??????????????? ??? ????????? ?????????
 .
.
-

? ????????? ????? ??????????? ???????? ???????
 .
.
-
??????
(
????.
loop) ?????????? ???????
 , ?????????? ??????, ? ???????? ???????? ??????? ?????????.
, ?????????? ??????, ? ???????? ???????? ??????? ?????????.
??????? ???????, ???? ?????????? ????????? E ????? ???? ?????, ?? ???? ?????????? ????????????
.
??????????
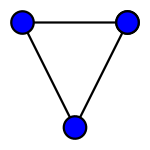
 ???????????????? ? ???????? ??????? (???????) ? ??????? (?????).
???????????????? ? ???????? ??????? (???????) ? ??????? (?????).
??????????
 ???? ???????????? ???? ???????? – ????????? ?????????
???? ???????????? ???? ???????? – ????????? ?????????
 ?
???????????????
?
???????????????
 ??????????????? ??? ????????? ????????? ?????????
??????????????? ??? ????????? ????????? ?????????
 .
.
-

-
???????? ???????
?????????? ?????????? ???????? ???????????????
 , ?? ???? ?????, ??? ???????? ??????? ?????????.
, ?? ???? ?????, ??? ???????? ??????? ?????????.
??????? ??????? ????
 ?? ?????????, ? ?????????, ?? ???? ????
?? ?????????, ? ?????????, ?? ???? ????
 ???????? ?????????? ????????, ?? ????? ???????? ?????????? ???????? ???????, ? ???? ?????????? ????????????
.
???????? ?????????? ????????, ?? ????? ???????? ?????????? ???????? ???????, ? ???? ?????????? ????????????
.
????????????????
????????????????
 ???? ???????????? ???? ???????? – ????????? ?????????
???? ???????????? ???? ???????? – ????????? ?????????
 ? ???????????????
? ???????????????
 ??????????????? ??? ????????? ?????????
??????????????? ??? ????????? ?????????
 .
.
-

??????? ???????, ????
 – ?????????, ?????????? ?????????? ???????? (??????? ?????), ?
– ?????????, ?????????? ?????????? ???????? (??????? ?????), ?
 ????? ????????? ?????, ?? ???? ?????????? ??????????????????
.
????? ????????? ?????, ?? ???? ?????????? ??????????????????
.
??????????????? ????
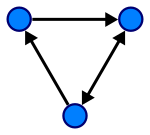 ??????????????? ????
??????????????? ????
??????????????? ???? (??????) (
????.
directed graph or dirgaph)
 ???? ???????????? ???? ???????? – ????????? ?????????
???? ???????????? ???? ???????? – ????????? ?????????
 ? ?????????
? ?????????
 ???
??? ????????????? ??? ????????? ????????? ?????????
???
??? ????????????? ??? ????????? ????????? ?????????

-
 .
.
????????? ? ????? ?????????????
-
 ,
,
??? ???????????
 ?????? ? ???????????? ?????? ???? ??
????????? ??????? (?????? ????)
?????? ? ???????????? ?????? ???? ??
????????? ??????? (?????? ????)
 , ? ???????????
, ? ???????????
 ?????? ? ???????????? ?????? ???? ??
???????? ??????? (????? ????)
?????? ? ???????????? ?????? ???? ??
???????? ??????? (????? ????)
 . ??????? ??? ????
. ??????? ??? ????
 ?????
??
?????
??
 ?
?

????????? ????
????????? ???? (
????.
Mixed graph)
 — ??? ???????????? ???? ???????? – ????????? ????????? ??????
— ??? ???????????? ???? ???????? – ????????? ????????? ??????
 , ? ????????? ???
, ? ????????? ???
 ??? ????????????? ??? ????????? ????????? ?????????
??? ????????????? ??? ????????? ????????? ?????????
 ? ????????? ?????
? ????????? ?????
 ??????????????? ??? ????????? ????????? ?????????
??????????????? ??? ????????? ????????? ?????????

-
 .
.
????????? ? ????? ?????????????
-

??????????????? ? ????????????????? ????? ???????? ???????? ???????? ??????????.
?????????? ?????
????
 ?????????? ?????????? ?????
?????????? ?????????? ?????
 , ???? ??????????
???????
, ???? ??????????
???????
 ?? ????????? ?????? ?????
?? ????????? ?????? ?????
 ? ????????? ?????? ?????
? ????????? ?????? ?????
 , ?????????? ????????? ?????????: ???? ? ?????
, ?????????? ????????? ?????????: ???? ? ?????
 ???? ????? ?? ???????
???? ????? ?? ???????
 ? ???????
? ???????
 , ?? ? ?????
, ?? ? ?????
 ?????? ???? ????? ?? ???????
?????? ???? ????? ?? ???????
 ? ???????
? ???????
 ? ???????? — ???? ? ?????
? ???????? — ???? ? ?????
 ???? ????? ?? ???????
???? ????? ?? ???????
 ? ???????
? ???????
 , ?? ? ?????
, ?? ? ?????
 ?????? ???? ????? ?? ???????
?????? ???? ????? ?? ???????
 ? ???????
? ???????
 . ? ??????
???????????????? ?????
??? ??????? ????? ?????? ????????? ?????????? ?????. ? ??????
??????????? ?????
??????? ????? ?????? ????????? ??? ?????.
. ? ??????
???????????????? ?????
??? ??????? ????? ?????? ????????? ?????????? ?????. ? ??????
??????????? ?????
??????? ????? ?????? ????????? ??? ?????.
?????? ????????? ???????????
?????????
? ????? ???????? ???????? ?????????????????? ??????, ? ??????? ?????? ??????? (????? ?????????) ????????? ?? ????????? ? ?????????????????? ???????? ??????.
?????
?????????? ??????? ??? ????????????? ?????.
??????? ?????
?????????? ??????? ??? ????????????? ?????? (?????? ???????, ??? ? ??????? ???? ??? ????????????? ?????).
??????????????? ?????????
(???
?????
) ? ??????? ???????? ???????? ?????????????????? ?????? ? ???, ? ??????? ?????? ??????? ?????????? ??????????? ? ????????????.
??????
???????? ????, ? ??????? ?????? ? ????????? ??????? ?????????. ??? ????
??????
???? (??? ?????) ???????? ????? ???????????? ???
?????
. ???????, ??? ???? ???????
 ?
?
 ???????? ??????? ?????????? ?????, ?? ???????? ??????? ???????????, ??????????????????
???????? ??????? ?????????? ?????, ?? ???????? ??????? ???????????, ??????????????????
 ???????? ??????. ????? ???????? ????? «???????????» ???????, ?????? ????????? ???????.
???????? ??????. ????? ???????? ????? «???????????» ???????, ?????? ????????? ???????.
???? (??? ????) ????????
???????
, ???? ????? ? ??? ?? ???????????;
????????????
, ???? ?? ??????? ? ??????? ? ??? ?? ??????????? (?? ??????????? ????????? ? ???????? ? ?????? ?????).
?????????? ???????? ????? ? ??????:
-
?????? ????, ??????????? ??? ???????, ???????? ???????????? ????, ??????????? ?? ?? ??? ???????;
-
?????? ???????
??????????????
???? ???????? ????????????
????
;
-
??????
???????
????, ?????????? ????? ????????? ??????? (??? ?????), ????????
????????????
(???-)????, ?????????? ????? ?? ?? ??????? (??? ?????);
-
????? — ???????????? ????.
???????? ?????????
?? ????????? ?????? ?????, ???????? ??? «?????????? ???? ??
 ?
?
 », ????????
?????????? ???????????????
?, ?????????????, ????????? ??? ????????? ?? ?????? ???????????????, ??????????
???????????? ?????????
?????. ???? ? ????? ????? ???? ?????????? ?????????, ?? ???? ???????. ?? ?????????? ????????? ????? ?????? ???????
??????????
????? ????????? ??? ??????????? ????? ????, ???????????? ??? ???????.
», ????????
?????????? ???????????????
?, ?????????????, ????????? ??? ????????? ?? ?????? ???????????????, ??????????
???????????? ?????????
?????. ???? ? ????? ????? ???? ?????????? ?????????, ?? ???? ???????. ?? ?????????? ????????? ????? ?????? ???????
??????????
????? ????????? ??? ??????????? ????? ????, ???????????? ??? ???????.
?????? ???????????? ??????? ??????? ?????
 ??????????
??????? ???????????
(??? ?????? ???????????) ?????
??????????
??????? ???????????
(??? ?????? ???????????) ?????
 . ????? «????????????» ???????? ???????????? ???????????? ?????????, ?? ???? ?? ???????????? ? ??????? ???????? ? ??????? ?????? ?????????.
. ????? «????????????» ???????? ???????????? ???????????? ?????????, ?? ???? ?? ???????????? ? ??????? ???????? ? ??????? ?????? ?????????.
????? ????? ??????????
??????
, ???? ??? ???????? ??????????? ????? ?????????.
?????????????? ?????????????? ??????
???? ??????????:
-
???????
, ???? ??? ????? ??????
 ,
,
 ???? ???? ??
???? ???? ??
 ?
?
 .
.
-
?????? ???????
???
?????????????? ???????
, ???? ?? ???????????????, ? ?? ????? ??????? ? ????? ?????? ??????? ??????????????? ????.
-
???????
, ???? ?? ??????? ? ?? ???????? ????????????? ??????.
-
??????
, ???? ????? ??? ??? (?????????, ???? ?? ??????????? ?????) ??????? ????????? ??????.
-
??????????
, ???? ??? ??????? ????? ??????? ?? ??? ???????????????? ????????????
 ?
?
 ???, ??? ?????? ????? ????????? ??????? ??
???, ??? ?????? ????? ????????? ??????? ??
 ? ???????? ??
? ???????? ??
 .
.
-
k-???????
, ???? ??? ??????? ????? ??????? ??
 ???????????????? ???????????
???????????????? ???????????
 ,
,
 , …,
, …,
 ???, ??? ?? ????? ?????, ??????????? ??????? ?????? ? ???? ?? ????????????.
???, ??? ?? ????? ?????, ??????????? ??????? ?????? ? ???? ?? ????????????.
-
?????? ??????????
, ???? ?????? ??????? ?????? ???????????? ????????? ?????? ? ?????? ???????? ??????? ????????????.
-
?????????
, ???? ???? ????? ?????????? ?????????? ?? ????????? ??? ??????????? ?????.
-
??????????
, ???? ??????? ????? ????? ?????????? ? ???????????? ????????? ?????, ?????????? ????? ?????.
-
??????????
, ???? ???? ?? ???????? ?????????????? ?????? ? ?????? ?????? ????.
????? ??????:
????????? ??????? ?????
??????? ???? ???????? ??????????
?????????????? ??????????
.
????? ??????????, ???? ????? ?????? ??? ??????
 , ???
, ???
 ?
?
 — ????????? ????????? (
??????
?
?????
, ?????.), ?
— ????????? ????????? (
??????
?
?????
, ?????.), ?
 —
??????? ?????????????
(???
??????????
), ?????????????? ??????? ?????
—
??????? ?????????????
(???
??????????
), ?????????????? ??????? ?????
 (????????????? ??? ???????????????) ???? ??????
(????????????? ??? ???????????????) ???? ??????
 ?
?
 ??
??
 (???
??????
). ???????? ???????? ????? ??????? ????????:
(???
??????
). ???????? ???????? ????? ??????? ????????:
??????? ????????????? ????? ? ???????????
??????? ?????????
???????, ??? ??? ???????, ??? ? ?????? ????????????? ???????? ?????. ? ?????? ?????? ???? ??????? ???????????? ?????, ???????????? ??????? ????? ?? ???????-?????? ? ???????-??????? (???? ????????).
??? ???????? ??????? ?????? ????????????? ??????? ??????.
??????????? ???????? ?????????? ? ??????, ????? ???????????????? ???????? ?????????? ??????.
-
????????? ??????;
-
??????? ? ??????????;
-
??????? ??????? (??? ?????? ???????).
??????? ?????????????
???????, ??? ?????? ????????????? ???????? ?????, ? ??????? ????????????? ?????? (??????) ?????. ? ?????? ??????? ?? ??????????? ??????
 ?? ????????
?? ????????
 ????????????:
????????????:
-
1
-
? ??????, ???? ?????
 «???????» ?? ???????
«???????» ?? ???????
 ,
,
-
?1,
-
???? ????? «??????» ? ???????,
-
0
-
?? ???? ????????? ??????? (?? ???? ???? ????? ???????? ?????? ??? ????? ?? ?????????? ???????)
?????? ?????? ???????? ???????? ????? (?????? ??????????????
 ) ??? ????????, ??????? ??????????? ????? ?????, ? ?????? ??????? (????????, ??? ???????? ?????????? ?????? ? ?????).
) ??? ????????, ??????? ??????????? ????? ?????, ? ?????? ??????? (????????, ??? ???????? ?????????? ?????? ? ?????).
?????? ?????????
??????, ??? ?????? ??????? ????? ????????????? ??????, ? ??????? ???????? ?????? ??????? ??????. ????? ????????? ?????? ?? ???????? ???????? ? ??????? ?????????, ? ???????????? ????? «?????? ???????».
?????? ?????????? ??????:
 .
.
??? ???????? ??????? ?????? ??? ????????????? ??????????? ??????, ? ????? ??? ?????????? ??????? ?????????? ?????? ????? ? ?????? ??? ???????, ??? ????? ?????? ???????? «???????» ??????? ??????????????? ???????.
?????? ?????
??????, ??? ??????? ????? ????? ????????????? ??????, ? ??????? ???????? ??? ???????, ??????????? ?????.
?????? ?????????? ??????:
 .
.
??? ???????? ?????????? ?????? ????????????? ??????, ??????? ????? ??????????? ??? ???????? ???????? ??? ?????? ???????.
????? ???????? ? ????????? ?????????? ??????
????? ????????
??? ???????? ??????, ?????????? ??? ???????? ????????? ? ???????????? ???????? ??? ????????????? ??????????, ???????????? ????????? ??????????????????? ??????, ????? ???????:
????????? ??? ??????????
??????????? ????? ???????????? ???????? ??? ?????????? ??????, ???, ?????????? ?????? ????? ? ?????? ?????????? ??????????? ??????? ?????
ILOG
(? 2009 ???? ??????????? ??????????
IBM
), ????? ?????? ???????? — GoView, Lassalle AddFlow, LEDA (???? ?????????? ????????).
????? ??????????
????????? ?????????
??? ?????????? ?????? ? ????????? ??????????
Boost
.
????????? ??? ????????????
???
???????????? ??????
??????????? ????????? ??????????? ????????:
-
Graphviz
(
Eclipse Public License
)
-
LION Graph Visualizer.
-
??????????????? — ????????????? ?????????, ? ??????? ???????????????? ??????????? (
GNU LGPL
; ?????? ??? Windows).
-
Gephi — ??????????? ???????? ??? ????????????? ? ???????? ?????? (
GNU GPL
,
CDDL
).
-
— ????????????? ????????? ??? ????????????? ? ???????? ?????? (
freeware
)
-
?????????? GraphX — ????????? ?????????? ???
.NET
??? ??????? ? ????????? ??????, ??????????
WPF 4.0
.
-
?????????? MSAGL — ????????? ?????????? ??? .NET
.
??. ?????
??????????
-
, ?. 3.
-
? , ?. 6.
-
(?????.)
. research.microsoft.com.
???? ?????????: 15 ?????? 2015.
14 ??? 2012 ????.
??????????
-
???????????? ?. ?.
?????? ??????. — ?????: ???????????? ???????? ???????????????? ????????????, 2014. — ?. 1. — 200 ?.
-
??????? ?.
?????? ??????. — ???????????: ???????????? ????????? ?????????? ??. ?. ?. ???????? ?? ???, 2002. — 336 ?. — ISBN 5-86134-101-?.
-
???????? ?. ?., ????????? ?. ?., ???????? ?. ?., ???????? ?. ?.
?????? ?? ?????? ??????. ?.: ?????, 1990. 384?. (???.2, ????. ?.: ????, 2009. 392 ?.)
-
???????? ?. ?., ?????????? ?.?.
????? ? ????????????????: ?????????, ???????????? ? ??????????. —
???.
: ???-?????????, 2003. — ?. 1104. —
ISBN 5-94157-184-4
.
-
???????? ?. ?.
????? ? Maple. —
?.
: ?????????, 2007. — 168 ?. —
ISBN 978-5-9221-0745-7
.
-
?????? ?. ?. ? ??.
????? VI. ????????? ??? ?????? ? ??????? // ?????????: ?????????? ? ?????? = Introduction to Algorithms. — 2-? ???. —
?.
: ???????, 2006. — ?. 1296. —
ISBN 0-07-013151-1
.
-
??? ?.
?????? ??????. —
?.
: ?????, 1968. — 336 ?.
-
????? // / ????. ?. ?. ?????. —
?.
:
??????????
, 1985. — ?. -88. — 352 ?.
-
????? ?. ?., ????????? ?. ?.
?????????????? ?????? ?????? ?????????? ??????. —
?.
: ??????-?????????????? ??????????, 1997. —
ISBN 5-02-015033-9
.
-
?????? ?.
???????? ? ?????? ??????. —
?.
: ???, 1977. — 208 ?.
-
?????? ?.
?????? ??????. —
?.
: ???, 1973.




