Interested Article - Кривая Гильберта

Кривая Гильберта (известная также как заполняющая пространство кривая Гильберта ) — это непрерывная фрактальная заполняющая пространство кривая , впервые описанная немецким математиком Давидом Гильбертом в 1891 году , как вариант заполняющих пространство кривых Пеано , открытых итальянским математиком Джузеппе Пеано в 1890 году .

Поскольку кривая заполняет плоскость, её размерность Хаусдорфа равна $2$ $2$ (в точности, её образ является единичным квадратом, размерность которого равна 2 при любом определении размерности, а её граф является компактным множеством, гомеоморфным замкнутому единичному интервалу с хаусдорфовой размерностью 2).

$H_{n}$ $H_n$ является $n$ $n$ -м приближением к предельной кривой. Евклидова длина кривой $H_{n}$ $H_n$ равна $\textstyle 2^{n}-{1 \over 2^{n}}$ $\textstyle 2^{n}-{1 \over 2^{n}}$ , то есть растёт экспоненциально от $n$ $n$ , будучи в то же время всегда в пределах квадрата с конечной площадью.

Рисунки

Кривая Гильберта, первый шаг
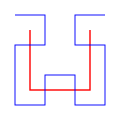
Кривые Гильберта, первый и второй шаги
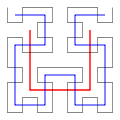
Кривые Гильберта, с первого по третий шаги
Ниточная графика
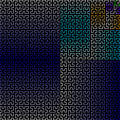
Кривая Гильберта в цвете

Трёхмерная кривая Гильберта
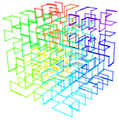
Трёхмерная кривая Гильберта в цвете, указывающем последовательность
Анимационная иллюстрация, показывающая прохождение кружков по кривой.

Приложения и алгоритмы отображения

Как истинная кривая Гильберта, так и её дискретная аппроксимация дают отображение одномерного и двумерного пространств, довольно хорошо сохраняющих локальные свойства . Если обозначить через ( x , y ) координаты точки в единичном квадрате, а через d расстояние вдоль кривой, на котором эта точка достигается, то точки, имеющие близкие к d значения, будут иметь также близкие значения и к ( x , y ). Обратное не всегда верно — некоторые точки, имеющие близкие координаты ( x , y ), имеют достаточно большую разницу в расстоянии d .

Ввиду этого свойства локальности кривая Гильберта широко применяется в компьютерных программах. Например, диапазон IP-адресов , присвоенных компьютерам, можно представить в виде рисунка путём использования кривой Гильберта. Программа создания такого представления для определения цвета точек может преобразовать изображение из двумерного в одномерное, и кривая Гильберта иногда используется ввиду свойства локальности этой кривой, поскольку это позволяет сохранять близкие IP-адреса близкими на одномерном представлении. Чёрно-белая фотография может быть подвержена дизерингу при использовании меньшего числа градаций серого путём переноса остаточного значения величины яркости на следующую точку вдоль кривой Гильберта. Кривая Гильберта используется в этом случае, поскольку она не создаёт видимых глазом переходов яркости, которые получаются при построчном преобразовании. Кривые Гильберта в пространствах большей размерности являются представителями обобщений кодов Грея и иногда используются в похожих ситуациях с похожими целями. Для многомерных баз данных предлагается использовать порядок Гильберта вместо Z-порядка , поскольку он даёт лучшее сохранение локальности. Например, кривые Гильберта использовались для сжатия и ускорения индексов в виде R-дерева . Кривые Гильберта использовались также для сжатия информационных баз данных .

Полезно иметь алгоритм, позволяющий делать преобразование в обоих направлениях (как из ( x , y ) в d , так и из d в ( x , y )). Во многих языках программирования предпочтительнее использовать итерации, а не рекурсию. Следующая программа на языке C осуществляет отображение в обоих направлениях, используя итерации и битовые операции, а не рекурсию. Программа предполагает разбиение квадрата на n х n ячеек (квадратов со стороной 1), где n является степенью двойки. Координаты (0,0) принадлежат левому нижнему углу, а ( n -1, n -1) — правому верхнему углу. Расстояние d отсчитывается от левого нижнего угла (расстояние 0) и растёт до $n^{2}-1$ $n^{2}-1$ в правом нижнем углу.

//Преобразовать (x,y) к d int xy2d (int n, int x, int y) { int rx, ry, s, d=0; for (s=n/2; s>0; s/=2) { rx = (x & s) > 0; ry = (y & s) > 0; d += s * s * ((3 * rx) ^ ry); rot(s, &x, &y, rx, ry); } return d; } //Преобразовать d к (x,y) void d2xy(int n, int d, int *x, int *y) { int rx, ry, s, t=d; *x = *y = 0; for (s=1; s<n; s*=2) { rx = 1 & (t/2); ry = 1 & (t ^ rx); rot(s, x, y, rx, ry); *x += s * rx; *y += s * ry; t /= 4; } } //вращаем/отражаем квадрант void rot(int n, int *x, int *y, int rx, int ry) { if (ry == 0) { if (rx == 1) { *x = n-1 - *x; *y = n-1 - *y; } //Обмениваем x и y местами int t = *x; *x = *y *y = t; } }

Программа использует соглашения языка C : знак & означает побитную операцию AND (И), знак ^ — побитную XOR (ИЛИ), знак += означает оператор добавления к переменной, а знак /= — операцию деления переменной.

Функция xy2d работает сверху вниз, начиная со старших битов x и y , и начинает построение d со старших битов. Функция d2xy работает в противоположном направлении, начиная с младших битов d , и строит x и y с младших битов. Обе функции используют функцию вращения и отражения системы координат ( x , y ).

Оба алгоритма работают похожим образом. Весь квадрат рассматривается как 4 области 2 х 2. Каждая область состоит из 4 меньших областей и так далее до конечного уровня. На уровне s каждая область имеет s х s ячеек. Имеется единственный цикл FOR, пробегающий через уровни. На каждой итерации добавляется значение к d или к x и y , которое определяется областью (из четырёх), в которой находимся на данном уровне. Области задаются парой ( rx , ry ), где rx и ry принимают значение 0 или 1. Таким образом, область определяется 2 входными битами (либо двумя битами из d , либо по биту из x и y ), и по ним образуется два выходных бита. Также вызывается функция вращения, чтобы ( x , y ) можно было использовать на следующем уровне на следующей итерации. Для xy2d она начинается с верхнего уровня всего квадрата и движется вниз до нижнего уровня до индивидуальных ячеек. Для d2xy процесс начинается снизу с ячеек и движется вверх до полного квадрата.

Можно реализовать эффективно кривые Гильберта, даже если область не образует квадрат . Более того, существуют некоторые обобщения кривых Гильберта для более высоких размерностей .

Представление в системе Линденмайера

Создание кривой Гильберта можно переписать для L-системы .

Шестая итерация создания кривой Гильберта

Алфавит : A, B

Константы : F + −

Аксиома : A

Правила :

A → − B F + A F A + F B −

B → + A F − B F B − F A +

Здесь F означает «движение вперёд», «−» означает поворот влево на 90° , «+» означает поворот вправо на 90° (см. turtle graphics ), а A и B игнорируются при рисовании.

Другие реализации

Arthur Butz дал алгоритм вычисления кривой Гильберта в многомерных пространствах.

В книге Graphics Gems II обсуждается кривая Гильберта и даётся реализация.

На основе кривой Гильберта могут быть реализованы вибраторные либо печатные конструкции антенн .

См. также

Примечания

, с. 459—460.
, с. 157—160.
, с. 124—141.
, с. 500—509.
, с. 1—12.
.
, с. 155—163.
, с. 295—312.
, с. 63—73.
, с. 424—42.
, с. 26—30.
Слюсар, В. (неопр.) Электроника: наука, технология, бизнес. — 2007. — № 6. С. 82—89. (2007). Дата обращения: 22 апреля 2020. 3 апреля 2018 года.

Литература

I. Kamel, C. Faloutsos. / Jorge Bocca, Matthias Jarke, Carlo Zaniolo. — San Francisco, CA, USA: Morgan Kaufmann Publishers Inc., 1994. — ISBN 1-55860-153-8 .
G.Peano. // Mathematische Annalen . — 1890. — Вып. 36 .
D. Hilbert. // Mathematische Annalen . — 1891. — Вып. 38 .
A.R. Butz. Alternative algorithm for Hilbert’s space filling curve. // IEEE Trans. On Computers. — 1971. — Т. 20 . — doi : .
B. Moon, H.V. Jagadish, C. Faloutsos, J.H. Saltz. Analysis of the clustering properties of the Hilbert space-filling curve // IEEE Transactions on Knowledge and Data Engineering. — 2001. — Т. 13 , вып. 1 . — doi : .
I. Kamel, C. Faloutsos. Proceedings of the 20th International Conference on Very Large Data Bases. — San Francisco, CA, USA: Morgan Kaufmann Publishers Inc., 1994.
T. Eavis, D. Cueva. A Hilbert space compression architecture for data warehouse environments // Lecture Notes in Computer Science. — 2007. — Т. 4654 .
Daniel Lemire, Owen Kaser. Reordering Columns for Smaller Indexes // Information Sciences. — 2011. — Т. 181 , вып. 12 . — arXiv : .
C. H. Hamilton, A. Rau-Chaplin. Compact Hilbert indices: Space-filling curves for domains with unequal side lengths // Information Processing Letters. — 2007. — Т. 105 , вып. 5 . — doi : .
J. Alber, R. Niedermeier. On multidimensional curves with Hilbert property // Theory of Computing Systems. — 2000. — Т. 33 , вып. 4 . — doi : .
H. J. Haverkort, F. van Walderveen,. Proceedings of the Eleventh Workshop on Algorithm Engineering and Experiments. — New York: Society for Industrial and Applied Mathematics (SIAM), 2009. — ISBN 9781615671489 .
Douglas Voorhies. Space-Filling Curves and a Measure of Coherence / Andrew S. Glassner. — Boston, San Diego, New York, London, Sydney, Tokyo, Toronto: AP Professional, 1991. — Т. II. — (Graphics Gems). — ISBN 0-12-059756-X .