Interested Article - Цветовая модель

Цветовая модель — математическая модель описания представления цветов в виде кортежей чисел (обычно из трёх, реже — четырёх значений), называемых цветовыми компонентами или цветовыми координатами . Все возможные значения цветов, задаваемые моделью, определяют цветовое пространство .

Цветовая модель задаёт соответствие между воспринимаемыми человеком цветами, хранимыми в памяти, и цветами, формируемыми на устройствах вывода (возможно, при заданных условиях).

Цветовое пространство CIE XYZ

Функции цветового соответствия Стандартного колориметрического наблюдателя, определённые комитетом CIE в 1931 году на диапазоне длин волн от 380 до 780 нм (с 5 нм интервалом)

Человек является — сетчатка глаза имеет три вида рецепторов (колбочек) , ответственных за цветное зрение . Можно считать, что каждый вид колбочек даёт свой отклик на определённую длину волны видимого спектра .

Важным свойством (для всех физически реализуемых цветов) является неотрицательность как функций отклика, так и результирующих цветовых координат для всех цветов. Системой, основанной на откликах колбочек человеческого глаза, является цветовая модель LMS .

Исторически сложилось, что для измерения цвета используется другое цветовое пространство — XYZ — эталонная цветовая модель, заданная в строгом математическом смысле Международной комиссией по освещению ( фр. Commission internationale de l'éclairage, CIE) в 1931 году. Модель CIE XYZ является мастер-моделью практически всех остальных цветовых моделей, используемых в технических областях.

Эксперименты, проведённые Дэвидом Райтом ( англ. David Wright) и Джоном Гилдом ( англ. John Guild) в конце 1920-х и начале 1930-х годов, послужили основой для определения функций цветового соответствия. Изначально функции цветового соответствия были определены для 2-градусного поля зрения (использовался соответствующий колориметр ). В 1964 году комитет CIE опубликовал дополнительные данные для 10-градусного поля зрения. Итак, аналогично координатам LMS, цвет XYZ задаётся следующим образом:

X=\int _{380}^{780}I(\lambda)\,{\overline {x}}(\lambda)\,d\lambda

X=\int _{380}^{780}I(\lambda)\,{\overline {x}}(\lambda)\,d\lambda

Y=\int _{380}^{780}I(\lambda)\,{\overline {y}}(\lambda)\,d\lambda

Y=\int _{380}^{780}I(\lambda)\,{\overline {y}}(\lambda)\,d\lambda

Z=\int _{380}^{780}I(\lambda)\,{\overline {z}}(\lambda)\,d\lambda

Z=\int _{380}^{780}I(\lambda)\,{\overline {z}}(\lambda)\,d\lambda

где

I(\lambda)

I(\lambda)

— спектральная плотность какой-либо энергетической фотометрической величины, например, потока излучения, энергетической яркости и т. п., в абсолютном или относительном выражении.

Для модели брались условия, чтобы компонента Y соответствовала визуальной яркости сигнала ( ${\overline {y}}(\lambda)$ ${\overline {y}}(\lambda)$ — эта та самая относительная спектральная световая эффективность монохроматического излучения для дневного зрения , которая используется во всех световых фотометрических величинах ), координата Z соответствовала отклику S («short», коротковолновых, «синих») колбочек , а координата X была всегда неотрицательной. Кривые отклика нормируются таким образом, чтобы площадь под всеми тремя кривыми была одинаковой. Это делается для того, чтобы равномерный спектр, цвет которого в колориметрических условиях наблюдения принято считать белым, имел одинаковые значения компонент XYZ и в дальнейшем, при анализе цвета, было проще определять цветовой тон просто вычитая из цвета равные значения XYZ. Функции отклика и координаты XYZ также являются неотрицательными для всех физически реализуемых цветов. Очевидно, что не для каждого сочетания XYZ существует монохроматическая спектральная линия (соответствующий цвет радуги), которая бы соответствовала этим координатам. На графике справа X — красная кривая, Y — зелёная, Z — синяя.

Цветовое пространство XYZ не задает сразу отклики колбочек на сетчатке человека, являясь очень сильно преобразованной цветовой моделью с целью получить значения цвета и, соответственно, возможность отличать один спектр от другого, отталкиваясь от фотометрической яркости излучения (Y). Саму яркость Y интерпретировать как отклик «зелёных» колбочек нельзя, эта функция для дневного зрения, являющегося трехстимульным, задается всеми реальными откликами рецепторов. Изначально модель CIE 1931 XYZ получили путём преобразования модели CIE 1931 RGB, которая, в свою очередь, является следствием прямого эксперимента по смешиванию и визуальному сравнению излучений различных спектральных составов. Любая цветовая модель может быть преобразована в модель XYZ, так как данная модель определяет все правила смешивания цветов и задает ограничения, накладываемые на все спектральные составы излучений, которые имеют один цвет.

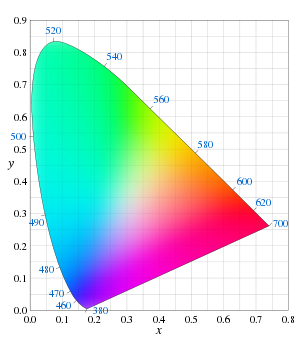
Хроматические координаты (x;y) и цветовое пространство xyY

Хроматическая диаграмма с длинами волн цветов

Если формально построить сечение пространства XYZ плоскостью $X+Y+Z=const$ $X+Y+Z=const$ , то можно две оставшиеся линейно-независимыми координаты записать в виде

x=X/(X+Y+Z)

x=X/(X+Y+Z)

y=Y/(X+Y+Z)

y=Y/(X+Y+Z)

.

аналогично, но необязательно:

z=Z/(X+Y+Z)

z=Z/(X+Y+Z)

Такое сечение называется хроматической диаграммой (диаграммой цветности).

В пространстве XYZ точке (X,0,0), как легко посчитать по формулам, на хроматической диаграмме соответствует точка xy=(1,0). Подобным образом, точке XYZ=(0,Y,0) соответствует точка xy=(0,1) и, наконец, точке XYZ=(0,0,Z) — точка xy=(0,0). Видно, что все реальные цвета, полученные любыми спектральными составами излучений, в том числе и монохроматическими (спектральные цвета) не дотягивают до подобных «чистых» значений. Данная закономерность вытекает из правила смешивания цветов и является проявлением того, что невозможно получить отклик одних колбочек без отклика других (хоть и очень малого), а также из того, что яркость Y не может иметь нулевое или малое значение при определенном отклике любых колбочек.

Цветовое пространство xyY можно задать, если задать значение цветности — (x, y) при данном значении яркости Y.

При этом для координат x и y продолжает выполняться условие неотрицательности.

Не следует путать светлоту Y в моделях XYZ и xyY — с яркостью Y в модели YUV или YCbCr .

Физически реализуемые цвета

Если на хроматической диаграмме xy отметить все возможные монохроматические цвета спектра, то они образуют собой незамкнутый контур, так называемый спектральный локус. Замыкание этого контура в основании «языка» называется линией пурпуров. Все цвета, которые могут быть реализованы в виде суммы спектральных линий данной яркости, будут лежать внутри этого контура. То есть существуют точки XYZ цветов за пределами контура, которые хотя и имеют положительные значения каждой компоненты, но тем не менее соответствующий отклик от колбочек не может быть получен при данной яркости (константе $Y=const$ $Y=const$ ).

Вместе с тем, при расчётах такие цвета (как и вообще цвета с отрицательными координатами) вполне могут использоваться. Например, в качестве базовых цветов для пространства Prophoto RGB были выбраны физически не реализуемые цвета.

Производные от CIE XYZ цветовые пространства

Цветовые модели можно классифицировать по их целевой направленности:

L*a*b* — равноконтрастное цветовое пространство, в котором расстояние между цветами соответствует мере ощущения их различия.
Аддитивные модели — где цвет получается путём добавления к черному (Класс RGB ).
Субтрактивные модели — получение цвета «вычитанием» краски из белого листа (, CMYK ).
Модели для кодирования цветовой информации при сжатии изображений и видео.
Математические модели, полезные для обработки изображения, например HSV .
Модели, где соответствие цветов задаётся таблично (Цветовая модель Пантон ( Pantone ))

Все модели сводятся к XYZ путём соответствующих математических преобразований. В качестве примеров можно рассмотреть:

Цветовая модель sRGB (IEC 61966-2.1) , разновидность модели RGB , широко используется в компьютерной индустрии, часто представляет собой цветовую модель «по умолчанию».
В телевидении для стандарта PAL применяется цветовая модель YUV , для SÉCAM — модель , а для NTSC — модель YIQ . (Следует помнить, что Y в этих моделях вычисляется совершенно по-другому, чем Y в модели XYZ).

Цветовой охват моделей устройств вывода

Охват различных устройств цветовоспроизведения

Диаграмма Yxy используется для иллюстрации характеристик цветового охвата (англ. color gamut ) различных устройств воспроизведения цвета — дисплеев и принтеров через соответствующие им цветовые модели.

Как уже было сказано, любой тройке чисел XYZ можно сопоставить конкретные координаты пространства RGB или CMYK. Так, цвет будет соответствовать яркости цветовых каналов или плотности красок. Физическая реализуемость цвета на устройстве накладывает условие неотрицательности координат. Таким образом, только некое подмножество Yxy может быть физически реализовано на устройстве. Эта область называется цветовым охватом устройства.

Конкретная область цветового охвата обычно имеет вид многоугольника, углы которого образованы точками основных , или первичных , цветов. Внутренняя область описывает все цвета, которые способно воспроизвести данное устройство.

На рисунке справа показаны области цветового охвата различных средств цветовоспроизведения:

белый контур отражает диапазон фотографической эмульсии различного назначения;
красный пунктирный контур — пространство sRGB, приблизительно соответствующее гамме большинства распространённых мониторов, являющиеся, по сути, стандартом представления графики в сети Интернет;
чёрный сплошной контур — пространство Adobe RGB, включающее цвета, воспроизводимые на печатных машинах, но с использованием первичных цветов;
синий сплошной контур соответствует высококачественной офсетной печати;
синий пунктирный контур отражает охват обычного бытового принтера.

См. также

Примечания

(неопр.) . Дата обращения: 3 июня 2008. Архивировано из 3 июня 2005 года.
William David Wright. A re-determination of the trichromatic coefficients of the spectral colours (англ.) // Transactions of the Optical Society. — 1928. — Vol. 30 . — P. 141—164 . — doi : .
John Guild. (англ.) // Philosophical Transactions of the Royal Society of London . — 1931. — Vol. A230 . — P. 149—187 .
(неопр.) . Дата обращения: 13 января 2010. 23 августа 2011 года.