«Перебрось мостик» , бридж-ит , «трубопровод» , «птичья клетка» , переключательная игра Шеннона или игра Гейла — абстрактная игра типа гекса для двух игроков . Игра придумана в середине XX века Дэвидом Гейлом; одновременно Клод Шеннон исследовал обобщённый вариант. В 1958 году Мартин Гарднер показал игру широкой публике в своей колонке в Scientific American . Хотя в бридж-ит можно играть и на бумаге, компания Hassenfeld Brothers (ныне Hasbro ) делала пластмассовые игральные комплекты .

Правила

• 
  1. Пустая доска
• 
  2. Красные победили
• 
  3. Выигрышная стратегия
• 
  4. Автомат, играющий в «перебрось мостик» (объяснение ниже по тексту)
• 
  5. «Графизация» игры, показывающая связь между классическим и обобщённым вариантом

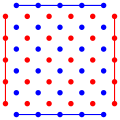
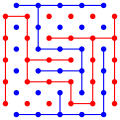
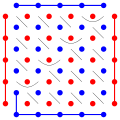
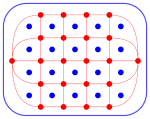
Игроки, красный и синий, проводят отрезки между двумя соседними точками своего цвета. Побеждает тот, кто сумел перебросить мостик от края до края доски: красный игрок по горизонтали, синий по вертикали.

Выигрышная стратегия

Первый игрок при правильной игре победит, это неконструктивно доказывается методом заимствования стратегии (синий-первый заимствует стратегию у синего-второго) с учётом симметрии доски.

Простую и красивую стратегию впервые предложил О. Гросс . Первый ход отмечен на рисунке 3. Когда второй игрок перечёркивает один конец тонкой чёрной линии, первый в ответ перечёркивает другой. По выражению Гросса, стратегия — «тупое оружие против тупого игрока, хитрое — против хитрого, но в том и другом случае ведёт к победе».

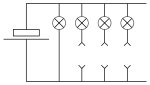
Такую стратегию можно реализовать даже простейшим автоматом из перемычек и лампочек, схема такого автомата показана на рисунке 4 . Первая лампочка подсвечивает первый ход автомата и горит постоянно. Остальные лампочки (ходы автомата) соединяются с гнёздами для перемычек (ходами человека), как показано на рисунке 3. Как только человек делает ход (вставляет перемычку в гнездо), загорается лампочка, означающая ответ автомата. Лампочки лучше располагать в вытянутых плафонах, имитирующих мостики. Если вдруг человек «смухлюет» и сделает свой ход поверх мостика автомата, то же самое сделает и автомат.

Стратегию Гросса удавалось поместить в 7 шагов калькулятора Б3-34 . Поскольку стратегия не требует никакой памяти, программа может вести сеанс одновременной игры .

Гекс , несмотря на внешнее сходство, совсем другая игра, поиск выигрышной стратегии для него — PSPACE -полная задача.

Обобщённый бридж-ит

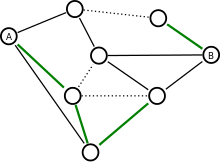
Если левую и правую красные кромки стянуть в две вершины, а верхнюю и нижнюю синие — «соединить проводом» и стянуть в одну, красная и синяя сетки становятся двойственными графами . Другими словами, красный соединяет вершины плоского графа без мостов , синий — грани того же графа (рисунок 5). Можно отказаться от ограничений на граф, если заставить синего не соединять грани, а стирать рёбра. Поэтому у обобщённой игры правила получаются такие:

Есть связный мультиграф , на котором отмечены две вершины А и Б. Игрок «Вырубить» своим ходом вырезает из графа ребро, игрок «Закоротить» фиксирует ребро, делая его неуязвимым к вырубанию. Закорачивающий выигрывает, если он смог зафиксировать маршрут от А до Б. Вырубающий — если он разделил эти вершины .

Легко видеть, что в зависимости от графа выигрывает «Вырубить», «Закоротить» или делающий первый ход. У обобщённого бридж-ита также существует стратегия, описанная на языке матроидов .

Примечания

Ссылки

• от 14 августа 2013 на Wayback Machine
• Глушанков Е., Певзнер П. (рус.) // Квант. — 1980. — № 9 . — С. 14—21 .