Си́льное ядерное взаимоде́йствие ( цветово́е взаимоде́йствие , я́дерное взаимоде́йствие ) — одно из четырёх фундаментальных взаимодействий в физике . В сильном взаимодействии участвуют кварки и глюоны и составленные из них частицы , называемые адронами ( барионы и мезоны ).

Оно действует в масштабах порядка размера атомного ядра и менее, отвечая за связь между кварками в адронах и за притяжение между нуклонами (разновидность барионов — протоны и нейтроны) в ядрах.

Благодаря сильному взаимодействию образуются ядерные силы , с помощью которых нуклоны могут образовывать стабильные системы — атомные ядра.

Пион-нуклонное взаимодействие

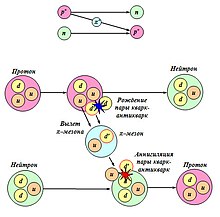
Необходимость введения понятия сильных взаимодействий возникла в 1930-х годах, когда стало ясно, что ни явление гравитационного , ни явление электромагнитного взаимодействия не могли ответить на вопрос, что связывает нуклоны в ядрах . В 1935 году японский физик Х. Юкава построил первую количественную теорию взаимодействия нуклонов, происходящего посредством обмена новыми частицами, которые сейчас известны как пи- мезоны (или пионы ). Пионы были впоследствии открыты экспериментально в 1947 году .

В этой пион-нуклонной теории притяжение или отталкивание двух нуклонов описывалось как испускание пиона одним нуклоном и последующее его поглощение другим нуклоном (по аналогии с электромагнитным взаимодействием, которое описывается как обмен виртуальным фотоном ). Эта теория успешно описала целый круг явлений в нуклон-нуклонных столкновениях и , а также в столкновениях пионов с нуклонами. Численный коэффициент, определяющий «эффективность» испускания пиона, оказался очень большим (по сравнению с аналогичным коэффициентом для электромагнитного взаимодействия), что и определяет «силу» сильного взаимодействия .

Следствием пион-нуклонного взаимодействия между нуклонами является наличие в ядерных силах наряду с обычными силами ( силы Вигнера , которые возникают в результате обмена нейтральными пионами) обменной составляющей. Если состояние двух взаимодействующих нуклонов зависит от их пространственных и спиновых координат, то существует три различных способа такого обмена :

• нуклоны обмениваются пространственными координатами при неизменных спиновых переменных. Обусловленные таким обменом силы называются силы Майораны (обмен заряженными пионами при сохранении спина нуклонов);
• нуклоны обмениваются спиновыми переменными при неизменных пространственных координатах. Силы между нуклонами, возникающие при таком способе обмена, получили название силы Бартлетта (обмен нейтральными пионами);
• нуклоны одновременно обмениваются спиновыми и пространственными координатами. Возникающие при этом обменные силы носят название силы Гейзенберга (обмен заряженными пионами при изменении спина нуклонов).

Кроме этого, ядерные силы зависят от зарядовых координат и имеют тензорную составляющую.

Оператор потенциальной энергии при феноменологическом описании ядерного взаимодействия двух нуклонов при низких энергиях имеет вид:

${\displaystyle V({\vec {r_{1}}},{\vec {r_{2}}},{\hat {\sigma _{1}}},{\hat {\sigma _{2}}},{\hat {\tau _{1}}},{\hat {\tau _{2}}})=U_{1}({\vec {r}})+U_{2}({\vec {r}})({\hat {\sigma _{1}}}{\hat {\sigma _{2}}})+U_{3}({\vec {r}})S_{12}+({\hat {\tau _{1}}}{\hat {\tau _{2}}})\left\{U_{4}({\vec {r}})+U_{5}({\vec {r}})({\hat {\sigma _{1}}}{\hat {\sigma _{2}}})+U_{6}({\vec {r}})S_{12}\right\}}$ ,

где ${\displaystyle r=r_{1}-r_{2}}$ , ${\displaystyle {\vec {r_{1}}},{\vec {r_{2}}}}$ — пространственные координаты, ${\displaystyle {\hat {\sigma _{1}}},{\hat {\sigma _{2}}}}$ — операторы Паули, ${\displaystyle {\hat {\tau _{1}}},{\hat {\tau _{2}}}}$ — операторы изотопического спина.

Силам Майораны (обмен пространственными координатами) соответствует слагаемое с ${\displaystyle ({\hat {\sigma _{1}}}{\hat {\sigma _{2}}})({\hat {\tau _{1}}}{\hat {\tau _{2}}})}$ , силам Бартлетта (обмен спиновыми переменными) соответствует слагаемое с ${\displaystyle ({\hat {\sigma _{1}}}{\hat {\sigma _{2}}})}$ , силам Гейзенберга (обмен пространственными и спиновыми переменными) соответствует слагаемое с ${\displaystyle ({\hat {\tau _{1}}}{\hat {\tau _{2}}})}$ . Кроме того, оператор ${\displaystyle S_{12}}$ учитывает тензорное взаимодействие, ${\displaystyle ({\hat {\tau _{1}}}{\hat {\tau _{2}}})S_{12}}$ — тензорное обменное взаимодействие.

Ядерные силы

На расстояниях порядка ${\displaystyle r_{0}\approx 10^{-15}}$ м величина сильного взаимодействия между нуклонами, составляющими атомное ядро, настолько велика, что позволяет практически не принимать во внимание их электромагнитное взаимодействие (отталкивание). Вообще говоря, взаимодействие нуклонов в ядре не является «элементарным»; скорее оно является таким же неизбежным следствием наличия сильного взаимодействия между частицами, например, составляющими нуклон кварками, как силы Ван-дер-Ваальса — следствием существования электромагнетизма. В хорошем приближении потенциальная функция взаимодействия двух нуклонов описывается выражением

${\displaystyle U(r)=-k{\frac {\exp(-r/r_{0})}{r}},}$

в котором ${\displaystyle k}$ — константа сильного взаимодействия, обычно полагающаяся равной ${\displaystyle 1}$ в «системе констант» фундаментальных взаимодействий, где, например, постоянная электромагнитного взаимодействия равна постоянной тонкой структуры (такая потенциальная функция называется потенциалом Юкавы ). Модуль этой функции очень быстро убывает и на расстояниях бо́льших ${\displaystyle r_{0}}$ уже ничтожно мал.

Вообще радиус ядра можно определить по приближённой формуле

${\displaystyle R=r_{0}A^{1/3},}$

где ${\displaystyle A}$ — общее число нуклонов в ядре.

Отсюда можно, в частности, очень приближённо найти массу мезона как переносчика сильного взаимодействия (впервые это было сделано японским физиком Хидэки Юкавой ). Для этого, однако, придётся сделать пару предположений, которые при строгом рассмотрении могут показаться безосновательными. Предположим, что мезон испускается одним нуклоном, и, совершив один «оборот» по «краю» потенциальной ямы (первое такое предположение), поглощается другим. Максимальная и, значит, наиболее вероятная длина волны его при этом ${\displaystyle \lambda =2\pi r_{0}A^{1/3}}$ . Импульс мезона

${\displaystyle p_{m}={\frac {h}{2\pi r_{0}A^{1/3}}},}$

где ${\displaystyle h}$ — постоянная Планка. Если бы мы сейчас (для определения массы покоя мезона ${\displaystyle m_{m}}$ ) предположили, что она в точности равна его массе при движении в ядре, это было бы недооценкой. Точно так же, если бы мы предположили, что скорость мезона в ядре примерно равна скорости света, это было бы переоценкой. В грубом приближении будем надеяться, что, если мы положим импульс мезона равным ${\displaystyle m_{m}c}$ ( ${\displaystyle c}$ — скорость света в вакууме), обе «неточности» скомпенсируются. Тогда

${\displaystyle m_{m}={\frac {h}{2\pi cr_{0}A^{1/3}}}.}$

Теперь наиболее физически оправданным будет подставить сюда ${\displaystyle A=2}$ , ведь речь шла о двух нуклонах. Тогда

${\displaystyle m_{m}={\frac {h}{2\pi cr_{0}2^{1/3}}}\approx 2{,}8\times 10^{-28}}$ кг.

Это значение составляет примерно ${\displaystyle 306{,}5\,m_{e}}$ , где ${\displaystyle m_{e}}$ — масса электрона . В действительности же масса мезона , являющегося переносчиком ядерного взаимодействия, составляет приблизительно ${\displaystyle m_{m({\text{real}})}\approx 273\,m_{e}\approx 2{,}26\times 10^{-28}}$ кг — результат более точных вычислений с использованием уже «более совершенных» элементов аппарата квантовой механики (хотя, вероятно, можно было бы «подобрать» экзотический мезон с массой ${\displaystyle 306{,}5\,m_{e}}$ ).

Оценить среднюю скорость нуклонов в ядерном веществе можно на основе модели ферми-газа . Объём фазового пространства, соответствующий частицам в единице объёма «физического» пространства, импульс которых ${\displaystyle p\leqslant p_{0}}$ , где ${\displaystyle p_{0}}$ — искомый предельный импульс, равен ${\displaystyle 4\pi p_{0}^{3}/3}$ . Разделив его на ${\displaystyle h^{3}}$ , получим число «клеток», в которые можно поместить по два протона и по два нейтрона. Положив число протонов равным числу нейтронов, найдём

${\displaystyle 4{\frac {4\pi }{3}}\left({\frac {p_{0}}{h}}\right)^{3}={\frac {A}{V}},}$

где ${\displaystyle V}$ — объём ядра, получающийся из формулы для его радиуса ${\displaystyle R=r_{0}A^{1/3}}$ , где ${\displaystyle r_{0}\sim 1{,}23\times 10^{-15}}$ м. В результате получаем значение ферми-импульса:

${\displaystyle p_{0}=\left({\frac {3A\pi ^{2}}{2V}}\right)^{1/3}{\frac {h}{2\pi }}=\left({\frac {9\pi }{8}}\right)^{1/3}{\frac {h}{2\pi r_{0}}}\approx 1{,}52\,{\frac {\hbar }{r_{0}}}\approx 1,3\times 10^{-19}}$ кг ${\displaystyle \cdot }$ м ${\displaystyle /}$ с ${\displaystyle \approx 244}$ МэВ/ c .

При таком импульсе релятивистская кинетическая энергия составляет около 30 МэВ, а скорость, соответствующая релятивистскому импульсу Ферми ${\displaystyle p_{0}=m_{p}v/{\sqrt {1-v^{2}/c^{2}}}}$ , равна ${\displaystyle v\approx c/4}$ , где ${\displaystyle c}$ — скорость света ( ${\displaystyle m_{p}\approx 938}$ МэВ — масса протона). Таким образом, движение нуклонов в ядре имеет релятивистский характер .

Феноменология сильных взаимодействий адронов

В 1950-е годы было открыто огромное число новых элементарных частиц , большинство из которых обладали очень малым временем жизни . Все эти частицы были сильно взаимодействующими: сечения их рассеяния друг на друге были порядка сечений взаимодействия нуклонов и пионов, и заметно превышали сечения взаимодействия с электронами.

Среди этих адронов были как мезоны , так и барионы . Они обладали различными спинами и зарядами ; в их распределении по массам и в предпочитаемых проглядывалась некоторая регулярность, однако откуда она бралась — не было известно.

По аналогии с пион-нуклонным рассеянием была построена модель сильных взаимодействий этих адронов, в которой каждому типу взаимодействия, каждому типу распада соответствовала некоторая своя константа взаимодействия. Кроме того, некоторые из наблюдаемых зависимостей не удавалось объяснить, и они просто постулировались в виде «правил игры», которым подчиняются адроны (, сохранение изоспина и G-чётности , и т. д.). Несмотря на то, что в целом это описание работало, оно, безусловно, было неудовлетворительно с точки зрения теории: слишком многое приходилось постулировать, большое число свободных параметров вводилось совершенно произвольно и безо всякой структуры.

В середине 1960-х годов была обнаружена SU(3) симметрия свойств адронов, и стало понято, что принципиальных степеней свободы при «конструировании» адронов вовсе не так много. Эти степени свободы получили название кварков . Эксперименты, проведённые спустя несколько лет, продемонстрировали, что кварки — не просто абстрактные степени свободы адрона, а реальные частицы, составляющие адрон, которые несут его импульс , заряд , спин и т. д. Единственная проблема заключалась в том, как описать тот факт, что кварки не могут вылететь из адронов ни в каких реакциях.

Тем не менее, даже в отсутствие теоретически обоснованной динамической картины взаимодействия кварков, уже тот факт, что адроны — составные частицы, позволил объяснить многие из чисто эмпирических свойств адронов.

Сильные взаимодействия в КХД

В 1970-х годах была построена микроскопическая теория сильного взаимодействия кварков, которая получила название квантовая хромодинамика (КХД). Она строится следующим образом.

Постулируется , что каждый кварк обладает новым внутренним квантовым числом , условно называемым цветом . Более точно, в дополнение к уже имеющимся степеням свободы, кварку приписывается и определённый вектор состояния в комплексном трёхмерном . В духе калибровочного подхода, накладывается требование инвариантности наблюдаемых свойств нашего мира относительно унитарных вращений в цветовом пространстве кварков, то есть относительно элементов группы SU(3) . (Таким образом, КХД является теорией Янга — Миллса .) Возникающее при этом калибровочное поле и описывает взаимодействие кварков. Это поле удаётся проквантовать ; его кванты называются глюонами .

Поскольку каждый тип глюонов задаёт определённый вид вращения в цветовом пространстве, количество независимых глюонных полей равно размерности группы SU(3), то есть восьми. Однако все глюоны взаимодействуют со всеми кварками с одинаковой силой. По аналогии с электродинамикой , где «мощность» взаимодействия характеризуется постоянной тонкой структуры α , «мощность» сильного взаимодействия характеризуется единственной константой сильного взаимодействия ${\displaystyle \alpha _{s}}$ .

Подчеркнём, что глюоны взаимодействуют с цветом. Из-за того, что группа SU(3) неабелева , глюоны тоже обладают цветом , а значит, могут взаимодействовать и друг с другом: в теории появляются трёхглюонные и четырёхглюонные вершины . В этом принципиальное отличие свойств КХД от КЭД , где фотон не был заряженным, поэтому сам с собой не взаимодействовал. Заметим, что из кварков и антикварков можно составить комбинации, которые обладают «нулевым» цветом, то есть бесцветные. В такие состояния с глюонами не взаимодействуют.

Следующим важнейшим свойством КХД является антиэкранировка заряда . Групповые свойства SU(3) приводят к тому, что константа связи сильного взаимодействия ${\displaystyle \alpha _{s}}$ уменьшается с уменьшением расстояния между кварками и растёт при удалении кварков друг от друга.

Первая из этих зависимостей приводит к асимптотической свободе : кварки, пролетающие на очень малых расстояниях друг от друга, можно в первом приближении считать невзаимодействующими.

Обратная сторона медали: конфайнмент (пленение) кварков. Это значит, что кварки не могут удалиться друг от друга на расстояние, заметно превышающее некоторый радиус конфайнмента (порядка 1 фм ). Однако два бесцветных состояния могут удалиться друг от друга на произвольное расстояние, поскольку глюонные поля их не удерживают. В результате получается, что в реальном мире наблюдаются не свободные кварки, а их бесцветные комбинации, которые и отождествляются с адронами .

Будучи удалёнными на расстояние, превышающее радиус конфайнмента, адроны всё же могут взаимодействовать, однако уже не за счёт обмена глюонами, а за счёт обмена другими адронами. В частности, при низких энергиях наиболее сильным оказывается взаимодействие через обмен пи-мезонами (). Такое взаимодействие (которое, кстати, и удерживает нуклоны в ядрах), тоже по традиции называется сильным. Однако надо понимать, что это — «остаточное» сильное взаимодействие, аналогичное ван-дер-ваальсовому взаимодействию нейтральных атомов.

Сильные взаимодействия в высокоэнергетических реакциях

Имеется целый ряд высокоэнергетических процессов столкновения адронов , в которых отсутствует жёсткий масштаб, из-за чего вычисления по теории возмущений в рамках КХД перестают быть надёжными. Среди таких реакций — полные сечения столкновения адронов, упругое рассеяние адронов на небольшие углы, . С точки зрения кинематики , в таких реакциях достаточно большой является только полная энергия сталкивающихся частиц в их системе покоя, но не переданный импульс.

Начиная с 1960-х годов, основные свойства таких реакций успешно описываются феноменологическим подходом, основанным на теории Редже . В рамках этой теории, высокоэнергетическое рассеяние адронов происходит за счёт обмена некоторыми составными объектами — реджеонами . Наиболее важным реджеоном в этой теории является померон — единственный реджеон, вклад которого в сечение рассеяния не уменьшается с энергией.

В 1970-х годах оказалось, что многие свойства реджеонов можно вывести и из квантовой хромодинамики . Соответствующий подход в КХД называется подходом — Фадина — Кураева — Липатова ().

Текущее состояние в теории сильных взаимодействий

Теоретическое описание сильных взаимодействий — одна из наиболее разработанных и вместе с тем бурно развивающихся областей теоретической физики элементарных частиц . Несмотря на то, что фундаментальная природа сильных взаимодействий понята ( цветовое взаимодействие между кварками и глюонами , описываемое квантовой хромодинамикой ), математические законы, выражающие её, очень сложны, и потому во многих конкретных случаях вычисления из первых принципов оказываются (пока что) невозможными. В результате возникает эклектическая картина: рядом с математически строгими вычислениями соседствуют полуколичественные подходы, основанные на квантовомеханической интуиции, которые, однако, прекрасно описывают экспериментальные данные.

Наметим общую структуру современной теории сильных взаимодействий. Прежде всего, фундаментом теории сильных взаимодействий является квантовая хромодинамика . В этой теории фундаментальными степенями свободы являются кварки и глюоны , лагранжиан их взаимодействия известен. Подходы к описанию сильного взаимодействия существенно зависят от того, какой именно объект изучается. Можно выделить следующие основные группы:

• жёсткие адронные реакции , в которых основную роль играют именно кварки и глюоны и которые хорошо описываются теорией возмущений в КХД ;
• полужёсткие реакции , в которых для разумного описания приходится учитывать бесконечное число членов ряда теории возмущений, и в определённых предельных случаях это удаётся сделать.
• низкоэнергетические (мягкие) адронные реакции , в которых более разумными степенями свободы становятся связанные состояния кварков ( адроны ) и изучаются законы взаимодействия.
• статические свойства адронов , в которых, в зависимости от конкретного случая, могут использоваться разные подходы.

Ниже кратко охарактеризованы методы теории сильных взаимодействий в каждом случае (часть разделов запланирована).

Жёсткие адронные реакции

Все открытые до сих пор адроны укладываются в стандартную картину, в которой они являются бесцветными составными частицами, построенными из кварков и антикварков. Характерные энергии, связанные с этой внутренней кварковой структурой (то есть характерные энергии связи в потенциальных моделях) порядка ${\displaystyle Q_{0}=1}$ ГэВ. Возникает естественная классификация процессов столкновений адронов:

• если передача импульса существенно меньше ${\displaystyle Q_{0}}$ , то динамика внутренних степеней свободы адронов несущественна, и можно переформулировать теорию в виде эффективной адронной теории.
• если же передача импульса при рассеянии существенно больше этой величины, то речь идёт о жёсткой адронной реакции.

В этом случае речь идет о том, что с хорошей точностью адроны можно считать слабосвязанными, и рассеяние происходит между отдельными составляющими быстро движущихся адронов — партонами . Такое поведение называется асимптотической свободой и связано оно прежде всего с убыванием константы сильного взаимодействия при увеличении передачи импульса (именно за открытие этого явления была присуждена Нобелевская премия по физике за 2004 год ).

Партонная картина

Благодаря свойству асимптотической свободы высокоэнергетический адрон можно считать системой слабо взаимодействующих (а в нулевом приближении, вообще не взаимодействующих) объектов, получивших название партоны . Жёсткая реакция столкновения адронов A и B в этом случае рассматривается как жёсткое столкновение двух партонов ( i и j соответственно). Сечение такой реакции можно записать как

${\displaystyle \sigma (A+B)=\int \limits _{0}^{1}dx_{1}\,dx_{2}\,f_{i}^{A}(x_{1})f_{j}^{B}(x_{2})\cdot \sigma (i+j).}$

Здесь ${\displaystyle f_{i}^{A}(x_{1})}$ обозначает плотность партонов типа i в адроне A , несущих долю импульса ${\displaystyle x_{1}}$ этого адрона. Сущность приближения коллинеарной факторизации заключается в том, что партонные плотности в этом выражении не зависят от того, какую именно реакцию мы рассматриваем, а при вычислении сечения столкновения двух партонов ${\displaystyle \sigma (i+j)}$ оба партона считаются реальными (а не виртуальными). Такое приближение хорошо работает именно в области жёстких столкновений.

Партонная структура высокоэнергетических адронов сложнее кварковой структуры тех же адронов, но находящихся в покое. При ускорении , переводящим покоящийся адрон в быстро движущийся, не только изменяется распределение исходных («валентных») кварков по импульсам, но и генерируются глюоны, а также кварк-антикварковые пары (так называемые «морские кварки»).

Все эти партоны обладают своей долей суммарного импульса адрона, а также дают вклад в общий спин адрона. Уже при энергиях адронов в несколько ГэВ, глюоны переносят уже примерно половину всего импульса протона; с дальнейшим ростом энергии эта доля только возрастает.

Уравнение эволюции партонных плотностей

Динамически связанная система (а точнее, её фоковский вектор состояния ) не является инвариантной относительно преобразований Лоренца , поэтому переходя в другую систему отсчёта, мы наблюдаем изменение состава адрона. Можно условно сказать, что глюонный компонент появляется при высоких энергиях из той силы, что удерживала кварки в покоящемся адроне. Из этого становится понятно, что вычислить партонные плотности из первых принципов пока не представляется возможным, поскольку в КХД до сих пор не решена общая проблема связанных состояний. Однако в рамках теории возмущений в КХД можно выписать уравнение эволюции партонных плотностей при увеличении жёсткого параметра (как правило, квадрата переданного импульса). Это уравнение носит название уравнения Докшицера — Грибова — Липатова — Альтарелли — Паризи (уравнение ДГЛАП) .

КХД на решётке

— непертурбативный подход к квантовохромодинамическим расчётам, основанный на замене непрерывного пространства-времени дискретной решёткой и моделировании происходящих процессов с помощью метода Монте-Карло. Такие расчёты требуют использования мощных суперкомпьютеров , однако позволяют с достаточно высокой точностью рассчитывать параметры, вычисление которых аналитическими методами невозможно. Например, расчёт массы протона дал величину, отличающуюся от реальной менее чем на 2 % . КХД на решётке также позволяет с приемлемой точностью рассчитывать и массы других, в том числе и ещё не открытых адронов, что облегчает их поиск.

В 2010 году с помощью решёточных расчётов была резко уточнена оценка массы u и d -кварков: погрешность снижена с 30 % до 1,5 % .

Примечания

Литература

• Окунь Л. Б. Лептоны и кварки. — М. : Едиториал УРСС, 2005. — ISBN 5-354-01084-5 .
• H. Leutwyler. (англ.) // Lectures given at the International School of Subnuclear Physics Erice. — 2012. — arXiv : .

Ссылки

• Д. И. Вайсбурд. (неопр.) С. 33—34, 62—63. lib.tpu.ru и Издательство Томского политехнического университета (2010). — ISBN 978-5-98298-665-8 , УДК 53 (075.8), ББК 22. 3я73 . Дата обращения: 30 ноября 2012. 1 декабря 2012 года.
• Артур Давидович Чернин. (неопр.) С. 149. Google и Издательство Терра (2008). — ISBN 5275016131 , 9785275016130, УДК 52, ББК 22,61, 318 страниц всего . Дата обращения: 10 декабря 2012.
• J. R. Christman. (неопр.) . (2001). Дата обращения: 28 апреля 2011. 22 августа 2011 года.
• (профессор Черняк В. Л., 2013 г.)