Interested Article - Изоморфизм графов

В теории графов изоморфизмом графов $G=\left\langle V_{G},E_{G}\right\rangle$ $G=\left\langle V_{G},E_{G}\right\rangle$ и $H=\left\langle V_{H},E_{H}\right\rangle$ $H=\left\langle V_{H},E_{H}\right\rangle$ называется биекция между множествами вершин графов $f\colon \ V_{G}\rightarrow V_{H}$ $f\colon \ V_{G}\rightarrow V_{H}$ такая, что любые две вершины $u$ $u$ и $v$ $v$ графа $G$ $G$ смежны тогда и только тогда, когда вершины $f(u)$ $f(u)$ и $f(v)$ $f(v)$ смежны в графе $H$ $H$ . Здесь графы понимаются неориентированными и не имеющими весов вершин и ребер. В случае, если понятие изоморфизма применяется к ориентированным или взвешенным графам, накладываются дополнительные ограничения на сохранение ориентации дуг и значений весов. Если изоморфизм графов установлен, они называются изоморфными и обозначаются как $G\simeq H$ $G\simeq H$ .

Иногда биекция $f$ $f$ записывается в виде подстановки изоморфизма ${\begin{pmatrix}a_{1}&a_{2}&\dots &a_{n}\\f(a_{1})&f(a_{2})&\dots &f(a_{n})\end{pmatrix}}$ ${\begin{pmatrix}a_{1}&a_{2}&\dots &a_{n}\\f(a_{1})&f(a_{2})&\dots &f(a_{n})\end{pmatrix}}$ . Некоторые задачи обработки графов требуют не только проверки изоморфизма, но и выяснения его подстановки.

Отношение изоморфизма графов представляет собой отношение эквивалентности , определенное для графов, и позволяет произвести разбиение исходного класса всех графов на классы эквивалентности . Множество графов, изоморфных друг другу, называется , их число в зависимости от $n$ $n$ представляет собой последовательность в OEIS (1, 1, 2, 4, 11, 34, 156, 1044, 12346, ...).

В случае, если биекция $f$ $f$ отображает граф сам на себя (графы $G$ $G$ и $H$ $H$ совпадают), она называется автоморфизмом графа $G$ $G$ .

Существуют также смежные задачи теории графов, такие как поиск изоморфного подграфа и , принадлежащие к классу NP-полных . В смежных разделах математики существуют схожие проблемы, например изоморфизма проективных плоскостей и изоморфизма конечных групп , которые полиномиально сводятся к проблеме изоморфизма графов (возможность обратной полиномиальной сводимости в общем случае не доказана) .

Пример

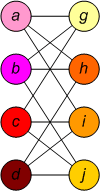
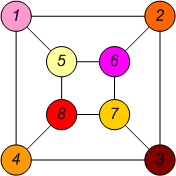
Два графа, приведенные в примере, являются изоморфными.

Граф $G$ $G$	Граф $H$ $H$	Изоморфизм между графами $G$ $G$ и $H$ $H$	Подстановка изоморфизма $f$ $f$
		$f(a)=1$ $f(a)=1$ $f(b)=6$ $f(b)=6$ $f(c)=8$ $f(c)=8$ $f(d)=3$ $f(d)=3$ $f(g)=5$ $f(g)=5$ $f(h)=2$ $f(h)=2$ $f(i)=4$ $f(i)=4$ $f(j)=7$ $f(j)=7$	${\begin{pmatrix}a&b&c&d&g&h&i&j\\1&6&8&3&5&2&4&7\end{pmatrix}}$ ${\begin{pmatrix}a&b&c&d&g&h&i&j\\1&6&8&3&5&2&4&7\end{pmatrix}}$

Изоморфизм графов общего вида

Графы $G$ $G$ и $H$ $H$ являются изоморфными, если путём перестановки строк и столбцов матрицы смежности графа $G$ $G$ удается получить матрицу смежности графа $H$ $H$ . Однако перебор всех возможных перестановок характеризуется вычислительной сложностью $O(N!)$ $O(N!)$ (при условии, что сравнение матриц смежности производится за время, не зависящее от $N$ $N$ , что обычно несправедливо и дополнительно увеличивает приведенную оценку), что существенно ограничивает применение подобного подхода на практике. Существуют методы ограниченного перебора возможных пар предположительно-изоморфных вершин (аналог метода ветвей и границ ), однако они незначительно улучшают приведенную выше асимптотику .

Теорема Уитни

Исключение из теоремы Уитни: представленные графы $K_{3}$ $K_{3}$ (слева) и $K_{1,3}$ $K_{{1,3}}$ (справа) не изоморфны, однако их рёберные графы изоморфны

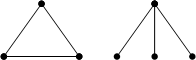
Теорема Уитни об изоморфизме графов , сформулированная Хасслером Уитни в 1932 году , гласит, что два связных графа изоморфны, тогда и только тогда, когда их рёберные графы изоморфны, за исключением графов $K_{3}$ $K_{3}$ (полного графа из 3 вершин) и полного двудольного графа $K_{1,3}$ $K_{{1,3}}$ , которые не являются изоморфными, однако оба имеют граф $K_{3}$ $K_{3}$ в качестве рёберного графа. Теорема Уитни может быть обобщена для гиперграфов .

Инварианты

Существует набор числовых характеристик графов, называемых инвариантами , которые совпадают у изоморфных графов (совпадение инвариантов является необходимым , но не достаточным условием наличия изоморфизма) . К ним относятся число вершин $n(G)$ $n(G)$ и число дуг/ребер $m(G)$ $m(G)$ графа G , упорядоченный по возрастанию или убыванию вектор степеней вершин $s(G)=(\rho (v_{1}),\rho (v_{2}),\dots ,\rho (v_{n}))$ $s(G)=(\rho (v_{1}),\rho (v_{2}),\dots ,\rho (v_{n}))$ , упорядоченный по возрастанию или убыванию вектор собственных чисел матрицы смежности графа (спектр графа), хроматическое число $\chi (G)$ $\chi (G)$ и др. Факт совпадения инвариантов обычно не несет информации о подстановке изоморфизма.

Инвариант называется полным , если совпадения инвариантов графов необходимо и достаточно для установления изоморфизма. Например, каждое из значений $\mu _{min}(G)$ $\mu _{{min}}(G)$ и $\mu _{max}(G)$ $\mu _{{max}}(G)$ (мини- и макси-код матрицы смежности) является полным инвариантом для графа с фиксированным числом вершин $n$ $n$ .

Различные инварианты имеют различную трудоемкость вычисления. В настоящее время полный инвариант графа, вычислимый за полиномиальное время, неизвестен, однако не доказано, что он не существует. Попытки его отыскания неоднократно предпринимались в 60-х — 80-х годах XX века , однако не увенчались успехом.

Модульное произведение Визинга

Модульное произведение графов $Y=G\lozenge H$ $Y=G\lozenge H$ , предложенное В. Г. Визингом , позволяет свести задачу проверки изоморфизма к задаче определения $\varphi (Y)$ $\varphi (Y)$ , содержащего $n(G)\cdot n(H)$ $n(G)\cdot n(H)$ вершин. Если $\varphi (Y)=n(G)$ $\varphi (Y)=n(G)$ , $n(G)\leq n(H)$ $n(G)\leq n(H)$ , то граф $H$ $H$ содержит подграф, изоморфный графу $G$ $G$ .

Изоморфизм графов специального вида

Вычислительная сложность

Хотя задача распознавания изоморфизма графов принадлежит классу NP , неизвестно, является ли она NP-полной или принадлежит классу P (при условии, что P ≠ NP ). При этом задача поиска изоморфного подграфа в графе является NP-полной . Современные исследования направлены на разработку быстрых алгоритмов решения как общей задачи изоморфизма произвольных графов, так и графов специального вида.

Применения

На практике необходимость проверки изоморфизма графов возникает при решении задач хемоинформатики , математической (компьютерной) химии , автоматизации проектирования электронных схем (верификация различных представлений электронной схемы ) , оптимизации программ (выделение общих подвыражений).

См. также

Ссылки

от 18 мая 2015 на Wayback Machine // Курс видео-лекций И. Пономаренко

Примечания

от 22 июня 2018 на Wayback Machine
↑ Курейчик В. М., Глушань В. М., Щербаков Л. И. Комбинаторные аппаратные модели и алгоритмы в САПР. — М. : Радио и связь, 1990. — 216 с.
H. Whitney. Congruent graphs and the connectivity of graphs // Am. J. Math.. — 1932. — Т. 54 . — С. 160-168 . — doi : .
Харари Ф. . — М. : Мир , 1973. 10 сентября 2011 года. (Изд. 3, М.: КомКнига, 2006. — 296 с.)
Dirk L. Vertigan, Geoffrey P. Whittle. // J. Comb. Theory, Ser. B. — 1997. — Т. 71 , вып. 2 . — С. 215-230 . — doi : . 28 февраля 2013 года.
Зыков А. А. . Основы теории графов. — М. : Наука, 1986. — 384 с. — ISBN 978-5-9502-0057-1 .
Трофимов М. И., Смоленский Е. А. Применение индексов электроотрицательности органических молекул в задачах химической информатики // Известия Академии наук. Серия химическая. — 2005. — С. 2166—2176 .