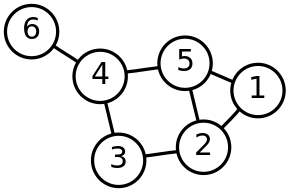
В теории графов контурный ранг неориентированного графа — это минимальное число рёбер, удаление которых разрушает все циклы графа, превращая его в дерево или лес. Контурный ранг можно понимать также как число независимых циклов в графе. В отличие от соответствующей задачи нахождения для ориентированных графов , контурный ранг r легко вычисляется по формуле

${\displaystyle r=m-n+c}$ ,

где m — число рёбер заданного графа, n — число вершин , а c — число компонент связности . Можно также эффективно построить множество рёбер минимального размера, разбивающих циклы, используя либо жадный алгоритм , либо дополнение остовного дерева .

Контурный ранг известен также как цикломатическое число графа. Его можно объяснить в терминах алгебраической теории графов как размерность циклического пространства графа, в терминах матроидов с использованием понятия коранга и в терминах топологии как одно из чисел Бетти топологического пространства, производного от графа. Контурный ранг подсчитывает число ушей в ушной декомпозиции графа, что даёт базис для понятия на почти деревьях и применяется в метриках программного обеспечения как часть определения цикломатической сложности фрагмента кода. Под названием цикломатическая сложность понятие было введено Густавом Кирхгофом .

Ранг матроида и построение минимального разрезающего циклы множества

Контурный ранг графа G можно описать с помощью теории матроидов как коранг для G . Если учесть свойство жадности матроидов, это означает, что можно найти минимальный набор рёбер, разрушающий все циклы, используя жадный алгоритм , выбирающий на каждом шаге ребро, принадлежащее по меньшей мере одному циклу оставшегося графа.

С другой стороны, минимальный набор множеств, разрушающий все циклы, можно найти путём построения остовного леса графа G и выбора дополняющего множества рёбер, не принадлежащих остовному лесу.

Число независимых циклов

В алгебраической теории графов , контурный ранг — это размерность пространства циклов графа ${\displaystyle G}$ . Интуитивно можно объяснить контурный ранг как подсчитывающий число независимых циклов графа, где набор циклов считается независим, если невозможно образовать один цикл как симметрическую разность некоторого поднабора других циклов .

Этот подсчёт независимых циклов может быть объяснён с помощью теории гомологий , ветви топологии . Любой граф G можно рассматривать как пример 1-мерного симплициального комплекса , одного из видов топологического пространства , образованного представлением каждого ребра графа отрезком и склеиванием этих отрезков на концах. Цикломатическое число является рангом первой (целой) группы гомологий этого комплекса ,

${\displaystyle r=\operatorname {rank} \left[H_{1}(G,\mathbb {Z})\right].}$

В связи с такой топологической связью цикломатическое число графа G называется также первым числом Бетти графа G . В более общем случае первое число Бетти любого топологического пространства подсчитывает число независимых циклов в пространстве.

Контурный ранг графа связан с рангом его матрицы инцидентности ${\displaystyle A}$ через соотношение ${\displaystyle r=m-\operatorname {rank} A}$ .

Приложения

Коэффициент сетчатости

Вариант контурного ранга планарного графа , нормализованный путём деления на максимально возможный контурный ранг любого планарного графа с тем же набором вершин, называется коэффициентом сетчатости . Для связных планарных графов с m рёбрами и n вершинами коэффициент сетчатости можно вычислить по формуле

${\displaystyle {\frac {m-n+1}{2n-5}}.}$

В этой формуле числитель ${\displaystyle m-n+1}$ в формуле является контурным рангом данного графа, а знаменатель ${\displaystyle 2n-5}$ является наибольшим возможным контурным рангом планарного графа с n вершинами. Коэффициент сетчатости лежит между 0 для деревьев и 1 для .

Ушная декомпозиция

Контурный ранг отражает число ушей в ушной декомпозиции графа, разложении рёбер графа на пути и циклы, что часто оказывается полезным в алгоритмах на графах. В частности, граф вершинно 2-связен тогда и только тогда, когда он имеет открытую ушную декомпозицию, последовательность подграфов, в котором первый подграф является простым циклом, а оставшиеся подграфы являются простыми путями и каждый путь начинается и кончается в вершинах, принадлежащих предыдущим подграфам, и каждая внутренняя вершина пути появляется первый раз в этом пути. В любом двусвязном графе с контурным рангом ${\displaystyle r}$ любая открытая ушная декомпозиция имеет в точности ${\displaystyle r}$ ушей .

Почти деревья

Граф с цикломатическим числом ${\displaystyle r}$ называется также почти r -деревом , поскольку нужно удалить из графа лишь r рёбер, чтобы превратить его в дерево или лес. Почти 1-дерево является почти деревом — связное почти дерево является псевдолесом , циклом с (возможно тривиальными) деревьями с корнями в каждой вершине .

Некоторые авторы изучали алгоритмах на почти r -деревьях с параметризацией по ${\displaystyle r}$ .

Обобщение для ориентированных графов

Циклический ранг — это инвариант ориентированных графов , измеряющий уровень вложенности циклов в графе. Этот инвариант имеет более сложное определение, чем цикломатический ранг (тесно связанный с определением глубины дерева для неориентированных графов) и вычисление его существенно сложнее. Другая задача для ориентированных графов, связанная с цикломатическим рангом — определение минимального , то есть минимального набора дуг, удаление которых разрушает все ориентированные циклы. Обе задачи, вычисление циклического ранга и определение минимального рарезающиего циклы набора дуг, являются NP-трудными .

Также можно вычислить более простой инвариант ориентированных графов, если игнорировать направления рёбер и вычислить циклический ранг неориентированного графа. Этот принцип образует базис для определения цикломатической сложности , меры сложности компьютерной программы для оценки сложности фрагмента компьютерного кода.

Связанные понятия

Другие числа, определяемые в терминах удаления рёбер из неориентированного графа, включают рёберной связности , минимальное число рёбер, удаление которых приводит к потере связности, и , минимальное число рёбер, удаление которых приводит к потере существования совершенного паросочетания .

Примечания

Литература

• Claude Berge. The Theory of Graphs. — Courier Dover Publications, 2001. — ISBN 9780486419756 .
• Claude Berge. Graphs and Hypergraphs. — Elsevier, 1976. — Т. 6. — (North-Holland Mathematical Library). — ISBN 9780720424539 .
• К. Берж. Теория графов и её применение.
• J. Buhl, J. Gautrais, R.V. Sole, P. Kuntz, S. Valverde, J.L. Deneubourg, G. Theraulaz. Efficiency and robustness in ant networks of galleries // The European Physical Journal B-Condensed Matter and Complex Systems. — Springer-Verlag, 2004. — Т. 42 , вып. 1 . — С. 123–129 . — doi : .
• H. Whitney. Non-separable and planar graphs // Transactions of the American Mathematical Society . — 1932. — Т. 34 . — С. 339–362 . — doi : . См. Теоремы 18 (связь ушной декомпозиции с циклическим рангом) и 19 (о существовании ушной декомпозиции)
• Richard A. Brualdi. Combinatorial matrix classes. — Cambridge: Cambridge University Press , 2006. — Т. 108. — С. 349. — (Encyclopedia of Mathematics and Its Applications). — ISBN 0-521-86565-4 .
• Don Coppersmith, Uzi Vishkin. Solving NP-hard problems in 'almost trees': Vertex cover // Discrete Applied Mathematics. — 1985. — Т. 10 , вып. 1 . — С. 27–45 . — doi : .
• Jiří Fiala, Ton Kloks, Jan Kratochvíl. Fixed-parameter complexity of λ-labelings // Discrete Applied Mathematics. — 2001. — Т. 113 , вып. 1 . — С. 59–72 . — doi : .
• Peter Robert Kotiuga. A Celebration of the Mathematical Legacy of Raoul Bott. — American Mathematical Soc., 2010. — С. 20. — ISBN 978-0-8218-8381-5 .
• Per Hage. Island Networks: Communication, Kinship, and Classification Structures in Oceania. — Cambridge University Press, 1996. — С. 48. — ISBN 978-0-521-55232-5 .
• Jean-Pierre Serre. Trees. — Springer, 2003. — С. 23. — (Springer Monographs in Mathematics).
• Gregory Berkolaiko, Peter Kuchment. Introduction to Quantum Graphs. — American Mathematical Soc., 2013. — С. 4. — ISBN 978-0-8218-9211-4 .