Interested Article - Базис

Ба́зис ( др.-греч. βάσις «основа») — упорядоченный (конечный или бесконечный) набор векторов в векторном пространстве или модуле , такой, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого набора. Векторы базиса называются базисными векторами .

В случае, когда базис бесконечен, понятие «линейная комбинация» требует уточнения. Это ведёт к двум основным разновидностям определения:

Базис Га́меля ( англ. Hamel basis), в определении которого рассматриваются только конечные линейные комбинации; применяется в основном в абстрактной алгебре.
Базис Ша́удера , в определении которого рассматриваются и бесконечные линейные комбинации, а именно — разложение в ряды ; применяется в основном в функциональном анализе, в частности, для гильбертова пространства .

В конечномерных пространствах оба определения базиса совпадают.

Происхождение термина

У Евклида и других древнегреческих математиков слово «базис» (βάσις, в значении основание ) обозначало горизонтальное основание плоской или пространственной фигуры. Современный математический смысл этому термину придал Дедекинд в статье 1885 года .

Базис на плоскости и в трёхмерном пространстве

Базис на плоскости. Базисные векторы изображены голубым и оранжевым цветом, зелёный вектор может быть представлен в виде суммы базисных векторов, умноженных на некоторые коэффициенты (зелёный = −2 голубой + 1 оранжевый), называемой линейной комбинацией и, таким образом, линейно зависим от них, как и любой другой вектор этого пространства (плоскости), каждый из которых тоже может быть представлен в виде линейной комбинации голубого и оранжевого с какими-то коэффициентами.

Любой декартовой системе координат на плоскости или в трёхмерном пространстве (также и в пространстве другой размерности) может быть сопоставлен базис, состоящий из векторов, каждый из которых направлен вдоль своей координатной оси. Это относится и к прямоугольным декартовым координатам (тогда соответствующий базис называется ортогональным ), так и к косоугольным декартовым координатам (которым будет соответствовать неортогональный базис).

Часто удобно выбрать длину ( норму ) каждого из базисных векторов единичной, такой базис называется нормированным.

Наиболее часто базис выбирают ортогональным и нормированным одновременно, тогда он называется ортонормированным .

В любом векторном пространстве базис можно выбрать различным образом (поменяв направления его векторов или их длины, например).

Обозначения

Обозначение векторов базиса может быть, в принципе, произвольным. Часто используют какую-нибудь букву с индексом (числовым или совпадающим с названием координатной оси), например:

{\vec {e}}_{1},{\vec {e}}_{2}

{\vec e}_{1},{\vec e}_{2}

или

{\vec {e}}_{x},{\vec {e}}_{y}

{\vec e}_{x},{\vec e}_{y}

— типичные обозначения базиса двумерного пространства (плоскости),

Декартовы координаты в трёхмерном пространстве ( *левая* (на рисунке слева) и *правая* (справа) декартовы системы координат (левый и правый базисы). Базисом, соответствующим такой системе координат, является тройка векторов, каждый из которых направлен вдоль какой-то из осей (три базисных вектора изображаются исходящими из общего начала).

{\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3}

{\vec e}_{1},{\vec e}_{2},{\vec e}_{3}

или

{\vec {e}}_{x},{\vec {e}}_{y},{\vec {e}}_{z}

\vec e_x, \vec e_y, \vec e_z

— трёхмерного пространства. Для трёхмерного пространства часто по традиции используется и обозначение

{\vec {i}},{\vec {j}},{\vec {k}}.

{\vec i},{\vec j},{\vec k}.

Представление какого-то конкретного (любого) вектора ${\vec {a}}$ $\vec a$ пространства в виде линейной комбинации векторов базиса (суммы базисных векторов числовыми коэффициентами), например

{\vec {a}}=a_{x}{\vec {e}}_{x}+a_{y}{\vec {e}}_{y}+a_{z}{\vec {e}}_{z}

{\vec a}=a_{x}{\vec e}_{x}+a_{y}{\vec e}_{y}+a_{z}{\vec e}_{z}

или

{\vec {a}}=a_{1}{\vec {e}}_{1}+a_{2}{\vec {e}}_{2}+a_{3}{\vec {e}}_{3}

{\vec a}=a_{1}{\vec e}_{1}+a_{2}{\vec e}_{2}+a_{3}{\vec e}_{3}

или, употребляя знак суммы $\Sigma$ $\Sigma$ :

{\vec {a}}=\sum _{i=1}^{3}a_{i}{\vec {e}}_{i}

{\vec a}=\sum _{{i=1}}^{3}a_{i}{\vec e}_{i}

называется разложением этого вектора по этому базису.

Числовые коэффициенты $(a_{x},a_{y},a_{z})$ $(a_{x},a_{y},a_{z})$ называются коэффициентами разложения, а их набор в целом — представлением (или представителем) вектора ${\vec {a}}$ $\vec a$ в базисе ${\vec {e}}_{x},{\vec {e}}_{y},{\vec {e}}_{z}.$ ${\vec e}_{x},{\vec e}_{y},{\vec e}_{z}.$ (Разложение вектора по конкретному базису единственно; разложение одного и того же вектора по разным базисам — разное, то есть получается разный набор конкретных чисел, однако в результате при суммировании — как показано выше — дают один и тот же вектор).

Виды базисов

Базис Гамеля

Базис Га́меля — множество векторов в линейном пространстве , таких, что любой вектор пространства может быть представлен в виде некоторой их конечной линейной комбинации ( полнота базиса), и такое представление для любого вектора единственно.

Критерием единственности решения задачи разложения вектора по полной системе векторов является линейная независимость векторов, входящих в полную систему. Линейная независимость означает, что всякая линейная комбинация векторов системы, в которой хотя бы один коэффициент ненулевой, имеет ненулевую сумму. То есть это эквивалентно единственности разложения нулевого вектора.

В случае линейных пространств, когда всякий ненулевой коэффициент обратим, линейная независимость эквивалентна невозможности выразить какой-либо вектор полной системы линейной комбинацией остальных векторов. (В более общей ситуации — модулей над кольцами — эти два свойства неэквивалентны). Невозможность выразить никакой вектор базиса через остальные означает минимальность базиса как полной системы векторов — при удалении любого из них теряется полнота.

В вопросе о существовании базисов основной является следующая лемма (доказательство этой леммы в общем случае неконструктивно и использует аксиому выбора ):

Лемма. Пусть $S_{1}$ $S_{1}$ — полная, а $S_{2}$ $S_{2}$ — линейно независимая система векторов. Тогда система $S_{1}$ $S_{1}$ содержит набор векторов, дополняющий $S_{2}$ $S_{2}$ до базиса пространства $V$ $V$ .

Доказательство

Доказательство строится на применении леммы Цорна. Рассмотрим $S=S_{1}\cup S_{2}$ $S=S_{1}\cup S_{2}$ . Пусть $L$ $L$ — множество всех линейно независимых подмножеств $S$ $S$ . Это множество частично упорядочено по отношению включения.

Докажем, что объединение любой цепи линейно независимых множеств остаётся линейно независимым. Действительно, возьмём вектора $a_{1},\ldots ,a_{n}$ $a_{1},\ldots ,a_{n}$ из объединения и возьмём множества из цепи, которым эти вектора принадлежат: $a_{1}\in A_{1},\ldots ,a_{n}\in A_{n}$ $a_{1}\in A_{1},\ldots ,a_{n}\in A_{n}$ . Так как эти множества — элементы цепи, их объединение даст максимальное из них, которое линейно независимо, а значит и вектора $a_{1},\ldots ,a_{n}$ $a_{1},\ldots ,a_{n}$ , лежащие в этом множестве, также линейно независимы.

Объединение множеств цепи линейно независимо, а значит, содержится в множестве $L$ $L$ . Применим к нему усиленную формулировку леммы Цорна , которая утверждает, что для каждого элемента из $L$ $L$ есть максимальный элемент больший или равный ему. $S_{2}\in L$ $S_{2}\in L$ , а значит, есть такой максимальный элемент $B\in L$ $B\in L$ , что $S_{2}\subset B$ $S_{2}\subset B$ . Легко видеть, что $B$ $B$ есть базис. Действительно, не будь $B$ $B$ полной системой векторов, был бы вектор $a\in S_{1}$ $a\in S_{1}$ , непредставимый как линейная комбинация векторов из $B$ $B$ . Тогда $B\cup \{a\}$ $B\cup \{a\}$ — линейно независимая система, а значит, $B\cup \{a\}\in L$ $B\cup \{a\}\in L$ , что противоречит тому, что $B$ $B$ —— максимальный элемент $L$ $L$ .

Следствием этой леммы являются утверждения:

Каждое линейное пространство обладает базисом.
Базис пространства можно выделить из любой полной системы векторов.
Всякую линейно независимую систему можно дополнить до базиса пространства V.

Любые два базиса в линейном пространстве равномощны , так что мощность базиса — величина, независящая от выбора базисных векторов. Она называется размерностью пространства (обозначается $\dim V$ $\dim V$ ). Если линейное пространство имеет конечный базис, его размерность конечна и оно называется конечномерным , в противном случае его размерность бесконечна, и пространство называется бесконечномерным.

Выбранный базис линейного пространства позволяет ввести координатное представление векторов, чем подготавливается использование аналитических методов.

Линейное отображение из одного линейного пространства в другое однозначно определено, если задано на векторах какого-нибудь базиса. Комбинация этого факта с возможностью координатного представления векторов предопределяет применение матриц для изучения линейных отображений векторных пространств (в первую очередь — конечномерных). При этом многие факты из теории матриц получают наглядное представление и приобретают весьма содержательный смысл, когда они выражены на языке линейных пространств. И выбор базиса при этом служит хоть и вспомогательным, но в то же время ключевым средством.

Примеры

Векторы $e_{1},e_{2},\dots ,e_{n}$ $e_{1},e_{2},\dots ,e_{n}$ пространства $\mathbb {R} ^{n}$ $\mathbb {R} ^{n}$ образуют базис тогда и только тогда, когда определитель матрицы, составленной из координатных столбцов этих векторов, не равен 0: $\det\{e_{1},e_{2},\dots ,e_{n}\}\neq 0$ $\det\{e_{1},e_{2},\dots ,e_{n}\}\neq 0$ .
В пространстве всех многочленов над полем один из базисов составляют степенные функции: $1,x,x^{2},\dots ,x^{n},\dots$ $1,x,x^{2},\dots ,x^{n},\dots$ .
Понятие базиса используется в бесконечномерном случае, например вещественные числа образуют линейное пространство над рациональными числами и оно имеет континуальный базис Гамеля и, соответственно, континуальную размерность.

Базис Гамеля и разрывная линейная функция

Базис Гамеля может быть использован для построения разрывной вещественной функции, удовлетворяющей условию $f(x+y)=f(x)+f(y)$ $f(x+y)=f(x)+f(y)$ . Пусть $\{r_{\alpha }\}$ $\{r_{\alpha }\}$ — базис Гамеля множества действительных чисел $\mathbb {R}$ $\mathbb {R}$ над полем рациональных чисел $\mathbb {Q}$ $\mathbb {Q}$ . Тогда для каждого $x=k_{\alpha _{1}}r_{\alpha _{1}}+\cdots +k_{\alpha _{n}}r_{\alpha _{n}}$ $x=k_{{\alpha _{1}}}r_{{\alpha _{1}}}+\cdots +k_{{\alpha _{n}}}r_{{\alpha _{n}}}$ ( $k_{i}\in \mathbb {Q}$ $k_{i}\in {\mathbb {Q}}$ ) положим $f(x)=k_{\alpha _{1}}f_{\alpha _{1}}+\cdots +k_{\alpha _{n}}f_{\alpha _{n}}$ $f(x)=k_{\alpha _{1}}f_{\alpha _{1}}+\cdots +k_{\alpha _{n}}f_{\alpha _{n}}$ , где $f_{\alpha _{n}}=f(r_{\alpha _{n}})$ $f_{\alpha _{n}}=f(r_{\alpha _{n}})$ произвольные вещественные числа, не все равные нулю одновременно; например, рациональные (в этом случае функция $f(x)$ $f(x)$ принимает лишь рациональные значения и тем самым гарантированно не является линейной функцией $f(x)=(c\cdot x)$ $f(x)=(c\cdot x)$ ). Такая функция $f(x)$ $f(x)$ аддитивна, то есть удовлетворяет функциональному уравнению Коши $f(x+y)=f(x)+f(y)$ $f(x+y)=f(x)+f(y)$ . Однако в общем случае, когда $f_{\alpha _{n}}\neq c\cdot r_{\alpha _{n}}$ $f_{\alpha _{n}}\neq c\cdot r_{\alpha _{n}}$ , она отличается от линейной функции $f(x)=c\cdot x$ $f(x)=c\cdot x$ и в силу этого является разрывной в любой точке, а также не сохраняет знак, не ни сверху, ни снизу, не монотонна , не интегрируема и не измерима на любом сколь угодно малом интервале, заполняя своими значениями на этом интервале всюдо плотно числовую ось $\left(-\infty ,+\infty \right)$ $\left(-\infty ,+\infty \right)$ .

Базис Шаудера

Система векторов $\{e_{n}\}$ $\{e_{n}\}$ топологического векторного пространства $L$ $L$ называется базисом Шаудера (в честь Шаудера ), если каждый элемент $f\in L$ $f\in L$ разлагается в единственный , сходящийся к $f$ $f$ ряд по $\{e_{n}\}$ $\{e_{n}\}$ :

f=\sum _{i=1}^{\infty }f_{i}e_{i},

f=\sum _{{i=1}}^{{\infty }}f_{i}e_{i},

где $f_{i}$ $f_{i}$ — числа, называемые коэффициентами разложения вектора $f$ $f$ по базису $\{e_{n}\}$ $\{e_{n}\}$ .

Чтобы подчеркнуть отличие определения базиса Гамеля для общих линейных пространств (допускаются только конечные суммы) от базиса Шаудера для топологических векторных пространств (допускается разложение в сходящийся ряд ), для первого часто используют термин линейный базис , оставляя термин базис для разложений в ряды . Мощность линейного базиса называют также линейной размерностью . В конечномерных пространствах эти определения совпадают из-за конечности базиса. В бесконечномерных пространствах эти определения существенно различаются и линейная размерность может быть строго больше мощности базиса Шаудера.

Например, никакое бесконечномерное Гильбертово пространство не имеет счетного линейного базиса, хотя может иметь счетные базисы Шаудера с разложением в ряд, в том числе, ортонормированные базисы . Все ортонормированные базисы гильбертовых пространств являются базисами Шаудера, например, множество функций $\{1,{\frac {1}{\sqrt {2}}}\sin(2\pi nx),{\frac {1}{\sqrt {2}}}\cos(2\pi nx)\mid n=1,2,\dots \}$ $\{1,{\frac {1}{{\sqrt {2}}}}\sin(2\pi nx),{\frac {1}{{\sqrt {2}}}}\cos(2\pi nx)\mid n=1,2,\dots \}$ является базисом Шаудера в пространстве $L^{2}[0,1]$ $L^{2}[0,1]$ . В более общих банаховых пространствах понятие ортонормированного базиса неприменимо, но часто удаётся построить базисы Шаудера, не использующие ортогональности.

Пример: базис Шаудера для пространства непрерывных функций C [ a, b ]

$C[a,b]$ $C[a,b]$ — банахово пространство с нормой $\|f\|=\max _{x\in [a,b]}|f(x)|$ $\|f\|=\max _{{x\in [a,b]}}|f(x)|$ . Для разложений в ряды Фурье и обобщенные ряды Фурье по ортонормированным системам функций легко доказывается сходимость в гильбертовом пространстве $L^{2}[a,b]$ $L^{2}[a,b]$ , но не в $C[a,b]$ $C[a,b]$ . Шаудер сконструировал базис Шаудера $\{e_{n}\}$ $\{e_{n}\}$ для $C[a,b]$ $C[a,b]$ . Пусть $\{x_{0},x_{1},\dots ,x_{n},\dots \}$ $\{x_{0},x_{1},\dots ,x_{n},\dots \}$ — плотное счетное множество точек на $[a,b]$ $[a,b]$ , $x_{0}=a$ $x_{0}=a$ , $x_{1}=b$ $x_{1}=b$ , остальные точки могут быть, например, всеми рациональными точками отрезка $[a,b]$ $[a,b]$ , упорядоченными произвольным образом. Положим: $e_{0}=1$ $e_{0}=1$ , $e_{1}=(x-a)/(b-a)$ $e_{1}=(x-a)/(b-a)$ — линейная функция. Определим кусочно-линейную функцию $e_{n}(x)$ $e_{n}(x)$ так, чтобы $e_{n}(x_{i})=0$ $e_{n}(x_{i})=0$ при $i=0,1,\dots ,n-1$ $i=0,1,\dots ,n-1$ и $e_{n}(x_{n})=1$ $e_{n}(x_{n})=1$ . Точки $x_{0},x_{1},x_{2},\dots ,x_{n-1}$ $x_{0},x_{1},x_{2},\dots ,x_{{n-1}}$ разбивают $[a,b]$ $[a,b]$ на $n-1$ $n-1$ отрезок. Точка $x_{n}$ $x_{n}$ лежит строго внутри одного из них. Пусть это $I_{n}=[x_{j},x_{k}]$ $I_{n}=[x_{j},x_{k}]$ для каких-то $j,k\in \{0,\dots ,n-1\}$ $j,k\in \{0,\dots ,n-1\}$ (порядок нумерации чисел $x_{0},x_{1},x_{2},\dots$ $x_{0},x_{1},x_{2},\dots$ не соответствует их величине).

Разложение непрерывной функции по базису Шаудера. Показано построение $L_{5}(x)$ $L_{{5}}(x)$ . Красным цветом на графике выделен участок, на котором $L_{5}$ $L_{{5}}$ отличается от $L_{4}$ $L_{{4}}$ (синяя ломаная).

Положим:

e_{n}(x)=0

e_{n}(x)=0

вне отрезка

I_{n}=[x_{j},x_{k}],

I_{n}=[x_{j},x_{k}],

e_{n}(x)={\frac {x-x_{j}}{x_{n}-x_{j}}}

e_{n}(x)={\frac {x-x_{j}}{x_{n}-x_{j}}}

при

x\in [x_{j},x_{n}],

x\in [x_{j},x_{n}],

e_{n}(x)={\frac {x_{k}-x}{x_{k}-x_{n}}}

e_{n}(x)={\frac {x_{k}-x}{x_{k}-x_{n}}}

при

x\in [x_{n},x_{k}].

x\in [x_{n},x_{k}].

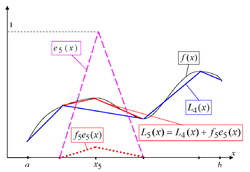
Полученная система кусочно-линейных «шапочек» и есть искомый базис Шаудера. Коэффициенты разложения произвольной функции $f(x)\in C[a,b]$ $f(x)\in C[a,b]$ по этому базису выражаются по явным рекуррентным формулам через последовательность значений $f(x_{i})$ $f(x_{i})$ . Частичная сумма первых $n+1$ $n+1$ членов ряда

L_{n}(x)=\sum _{i=0}^{n}f_{i}e_{i}(x),

L_{n}(x)=\sum _{{i=0}}^{{n}}f_{i}e_{i}(x),

является в данном случае кусочно-линейной аппроксимацией $f(x)$ $f(x)$ с узлами в точках $x_{0},x_{1},x_{2},\dots ,x_{n}$ $x_{0},x_{1},x_{2},\dots ,x_{{n}}$ ; формула для коэффициентов $f_{n}=f(x_{n})-L_{n-1}(x_{n});\;\;f_{0}=f(a)$ $f_{n}=f(x_{n})-L_{{n-1}}(x_{n});\;\;f_{0}=f(a)$ (см. Рис.)

Проблема базиса

Базисы Шаудера построены для большинства известных примеров банаховых пространств, однако проблема Банаха — Шаудера о существовании базиса Шаудера в каждом сепарабельном банаховом пространстве не поддавалась решению более 50 лет и лишь в 1972 году была решена отрицательно: существуют сепарабельные банаховы пространства без базиса Шаудера (контрпримеры Энфло , Шанковского, Дэви и Фигеля).

Применение в кристаллографии

В векторной алгебре с помощью векторного произведения и смешанного произведения определяется понятие взаимного базиса к базису в трёхмерном евклидовом пространстве и используется для доказательства некоторых утверждений, связанных со смешанным произведением и углами между векторами ^:212-214 . В кристаллографии взаимный базис называется кристаллографическим определением базиса , на основе которого определяется обратная решётка .

См. также

Репер — близкое понятие.
Ортогональный базис — специальный класс базисов (базисов Шаудера) для пространств со скалярным произведением ( Гильбертово пространство ).
Базис Грёбнера
Базис Рисса
Конечномерное пространство
Флаг (математика)

Примечания

Per Enflo. (англ.) // Acta Math.. — 1973. — Vol. 130 (1973) . — P. 309-317 . — doi : . 20 июля 2020 года.
перевод: Пер Энфло. = A counterexample to the approximation problem in Banach spaces // Математика / пер. Б. С. Митягина. — 1974. — Т. 18 , вып. 1 . — С. 146–155 .
Гусятников П.Б., Резниченко С.В. . — М. : Высшая школа , 1985. — 232 с. 10 января 2014 года.