Центральный вопрос теории узлов — являются ли две диаграммы отображением одного и того же узла . Один из инструментов, используемых для ответа на этот вопрос — многочлен узла , который является инвариантом узла . Если двум диаграммам отвечают различные многочлены , значит они представляют различные узлы. Обратное не всегда верно.

Скейн-соотношение (или соотношение типа Конвея ) часто используют, чтобы простым способом определить многочлен узла. Неформально говоря, скейн-соотношение задаёт линейную связь значений многочлена узла на трёх зацеплениях , которые отличаются друг от друга лишь в малой области. Для некоторых многочленов, таких как полиномы Конвея , Александера и Джонса , подходящего скейн-соотношения достаточно, чтобы вычислить многочлен рекурсивно . Для других, таких как полином HOMFLY , требуются более сложные алгоритмы.

Определение

В скейн-соотношении участвуют три диаграммы зацепления , идентичные всюду, кроме одного перекрёстка. Эти три диаграммы должны выражать три возможности, которые могли бы иметь место на этом перекрёстке: нить может пройти под другой нитью, над ней или не пересечься с ней вовсе. Необходимо рассматривать диаграммы зацеплений , поскольку изменение даже одного перекрёстка может превратить диаграмму узла в диаграмму зацепления и наоборот. В зависимости от конкретного многочлена узла, зацепления, появляющиеся в скейн-соотношении могут быть ориентированы или неориентированы.

Три диаграммы обозначаются следующим образом. Разверните узел так, чтобы направления обеих нитей в рассматриваемом пересечении указывали примерно на север. У одной диаграммы нить северо-западного направления будет проходить над северо-восточной нитью, её обозначим ${\displaystyle L_{-}}$ . У другой диаграммы северо-восточная нить проходит над северо-западной, это ${\displaystyle L_{+}}$ . Последняя диаграмма лишена этого перекрёстка и обозначается ${\displaystyle L_{0}}$ .

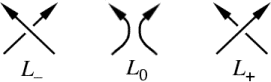
(На самом деле, обозначения не зависят от направления в том смысле, что при замене всех направлений на противоположные, обозначение остаётся прежним. Поэтому многочлены определяются однозначно и на неориентированных узлах. Однако ориентация на зацеплении принципиально важна, чтобы помнить в каком порядке выполнялась рекурсия.)

Полезно мыслить это как составление из одной диаграммы двух других наложением «заплаток» с соответствующими ориентациями.

Чтобы рекурсивно определить многочлен узла (зацепления), фиксируется функция ${\displaystyle F}$ и для любой тройки диаграмм и их полиномов, обозначенных, как было указано выше,

${\displaystyle F{\Big (}L_{-},L_{0},L_{+}{\Big)}=0}$

или более аккуратно

${\displaystyle F{\Big (}L_{-}(x),L_{0}(x),L_{+}(x),x{\Big)}=0}$ для каждого ${\displaystyle x}$ .

(Нахождение функции ${\displaystyle F}$ , которая делает многочлен независимым от очерёдности пересечений в рекурсии — непростая задача.)

Более формально, скейн-соотношение можно рассматривать, как определение ядра фактор-отображения из . Такое отображение соответствует многочлену узла, если все замкнутые диаграммы отображать в сложные виды пустых диаграмм.

Ссылки