Вакуум-дистилляция
- 1 year ago
- 0
- 0

Дистилля́ция (от лат. distillatio — стекание каплями; перегонка ) — процесс испарения жидкости с последующим охлаждением и конденсацией паров , который используется, прежде всего, для разделения жидких смесей и очистки выделяемых веществ. Основан на различии в температурах кипения компонентов смеси. В зависимости от состава разделяемой смеси и целей процесса, продуктами дистилляции могут быть как дистиллят (отогнанные фракции), обогащённый более летучими (низкокипящими) компонентами, так и неотогнанный (кубовый) остаток, содержащий менее летучие (высококипящие) компоненты .
Различают дистилляцию с конденсацией пара в жидкость (при которой получаемый дистиллят имеет усреднённый состав вследствие перемешивания) и дистилляцию с конденсацией пара в твёрдую фазу (при которой в конденсате возникает распределение концентрации компонентов).
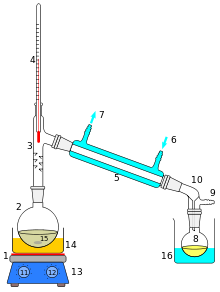
Основными деталями дистилляционного устройства являются испаритель, представляющий собой обогреваемый контейнер (куб) для перегоняемой жидкости, дефлегматор , для частичной конденсации пара, выходящего из испарителя, охлаждаемый конденсатор (холодильник), сборник дистиллята и соединяющий их паропровод .

Первые сведения о дистилляции относятся к I веку и упоминаются в работах греческих алхимиков в Александрии (Египет) . В XI веке, у Авиценны , дистилляция упоминается как метод получения эфирных масел . C середины XIX века разрабатывается ректификация .
Дистилляция применяется в промышленности и в лабораторной практике для разделения и рафинирования сложных веществ: для разделения смесей органических веществ (например, разделение нефти на бензин , керосин , дизельное топливо и др.; получение душистых веществ в парфюмерии; очистка этилового спирта ) и для получения высокочистых неорганических веществ (например, металлов : бериллия , свинца , цинка , магния , кадмия , ртути ; и неметаллов : серы , селена и др.).
В теории дистилляции в первую очередь рассматривается разделение смесей двух веществ . Принцип дистилляции основан на том, что концентрация некоторого компонента в жидкости отличается от его концентрации в паре этой жидкости. Отношение = является характеристикой процесса и называется коэффициентом разделения (или распределения) при дистилляции. (Также коэффициентом разделения при дистилляции называют величину ). Коэффициент разделения зависит от природы разделяемых компонентов и условий дистилляции. В зависимости от условий дистилляции различают идеальный (определяемый только парциальными давлениями паро́в чистых компонентов), равновесный (когда число частиц, покидающих в единицу времени жидкость, равно числу частиц, возвращающихся в это же время в жидкость) и эффективный коэффициенты разделения. Практически дистилляция веществ сильно зависит от интенсивности перемешивания жидкости, а также от взаимодействия примесей с основным компонентом и с другими примесными компонентами с образованием соединений (в связи с чем дистилляция считается физико-химическим процессом). Эффективный коэффициент разделения смеси «основное вещество — примесь» может на несколько порядков отличаться от идеального коэффициента разделения.
Режимы дистилляции характеризуются температурой испарения и степенью отклонения от фазового равновесия жидкость-пар. Обычно в дистилляционном процессе , где — число частиц вещества, переходящих в единицу времени из жидкости в пар, — число частиц, возвращающихся в это же время из пара в жидкость, — число частиц, переходящих в это время в конденсат. Отношение является показателем отклонения процесса от равновесного. Предельными являются режимы, в которых (равновесное состояние системы жидкость-пар) и (режим молекулярной дистилляции).
Идеальный коэффициент разделения двухкомпонентного вещества может быть выражен через давления и чистых компонентов при температуре процесса: . С учётом коэффициентов активности компонентов и , отражающих взаимодействие компонентов в жидкости, коэффициент разделения . Коэффициенты активности имеют температурную и концентрационную зависимости (см. активность (химия) ). С понижением температуры значение коэффициента разделения обычно удаляется от единицы, то есть эффективность разделения при этом увеличивается.
При все испаряющиеся частицы переходят в конденсат (режим молекулярной дистилляции). В этом режиме коэффициент разделения , где и — молекулярные массы первого и второго компонентов соответственно. Определение молекулярного режима дистилляции возможно по величине , где — расстояние от испарителя до конденсатора, — длина свободного пробега молекул дистиллируемого вещества, — константа, зависящая от конструкции аппарата. При наблюдается молекулярное испарение, при между жидкостью и паром устанавливается динамическое равновесие, а при других значениях испарение имеет промежуточный характер. Режим молекулярной дистилляции может применяться в различных дистилляционных способах, включая ректификацию . Обычно молекулярная дистилляция осуществляется в вакууме при низком давлении пара и при близком расположении поверхности конденсации к поверхности испарения (что исключает столкновение частиц пара друг с другом и с частицами атмосферы). В режиме, близком к молекулярной дистилляции, проводится дистилляция металлов. В связи с тем, что коэффициент разделения при молекулярной дистилляции зависит не только от парциальных давлений компонентов, но и от их молекулярных (или атомных) масс, молекулярная дистилляция может применяться для разделения смесей, для которых , — азеотропных смесей , включая смеси изотопов .
В общем случае, математическое описание дистилляции (и сублимации) представляется в виде системы уравнений, содержащих два параметра: эффективный коэффициент разделения β и диффузионное число Пекле Ре=w(T)X / ρD(T) , где w - скорость испарения вещества с единицы поверхности; D - коэффициент диффузии примеси; X - размерный фактор испаряемого материала (например, толщина слоя испаряемого материала); ρ - плотность вещества. Ввиду сложности уравнений, их решение может быть найдено только численными методами. В простом случае, когда дистилляция осуществляется в условиях интенсивного перемешивания испаряемой жидкости (и конденсата), когда Ре= 0 или мало, уравнения, связывающие содержание второго компонента в конденсате и в остатке с долей перегонки или с долей остатка при заданных условиях процесса и известной начальной концентрации жидкости ( , и — масса конденсата и остатка, а также начальная масса дистиллируемого вещества соответственно), имеют простой вид с одним параметром β.
При дистилляции вещества с большой концентрацией компонентов (с конденсацией пара в жидкость), при несильной зависимости коэффициентов активности компонентов от их концентраций взаимосвязь величин , и , когда используются концентрации в процентах, имеет вид:
Для дистилляции с конденсацией пара в жидкость при малом содержании примеси
где — коэффициент разделения.
Также выведены уравнения распределения компонентов в твёрдом конденсате, получаемого дистилляцией с направленным затвердеванием конденсата или зонной дистилляцией.
Отмечено, что дистилляционные уравнения описывают не только процессы распределения компонентов в системах "жидкость - пар", но и в других контактирующих фазах (например, переходы "жидкий кристалл - кристалл", "жидкий кристалл-жидкость", "газ - плазма", а также переходы, связанные с квантово-механическими состояниями — сверхтекучая жидкость , конденсат Бозе — Эйнштейна ) — при подстановке в них соответствующих коэффициентов разделения.
Простая перегонка — частичное испарение жидкой смеси путём непрерывного отвода и конденсации образовавшихся паров в холодильнике. Полученный конденсат называется дистиллятом, а неиспарившаяся жидкость — кубовым остатком.
Фракционная дистилляция (или дробная перегонка) — разделение многокомпонентных жидких смесей на отличающиеся по составу части, фракции, путём сбора конденсата частями с различной летучестью, начиная с первой, обогащенной низкокипящим компонентом. Остаток жидкости обогащён высококипящим компонентом. Для улучшения разделения фракций применяют дефлегматор .
Ректификация — способ дистилляции, при котором часть жидкого конденсата (флегма) постоянно возвращается в куб, двигаясь навстречу пару в колонне . В результате этого примеси, содержащиеся в паре, частично переходят во флегму и возвращаются в куб, при этом чистота пара (и конденсата) повышается.
Дистилляция с конденсацией пара в градиенте температуры — дистилляционный процесс, в котором конденсация в твёрдую фазу осуществляется на поверхности, имеющей градиент температуры, с многократным реиспарением частиц пара. Менее летучие компоненты осаждаются при более высоких температурах. В результате в конденсате возникает распределение примесей вдоль температурного градиента, и наиболее чистая часть конденсата может быть выделена в качестве продукта. Разделение компонентов пара при реиспарении подчиняется собственным закономерностям. Так, при молекулярной дистилляции соотношение между количествами и осаждённых в конденсаторе первого и второго компонентов, соответственно, выражается равенством:
где и — скорости испарения первого компонента из расплава и с поверхности реиспарения соответственно, и — то же для второго компонента, и — коэффициенты конденсации первого и второго компонентов соответственно, — коэффициент, зависящий от поверхности испарения и углов испарения и реиспарения. Реиспарение повышает эффективность очистки от трудноудаляемых малолетучих примесей в 2—5 раз, а от легколетучих — на порядок и более (по сравнению с простой перегонкой). Этот вид дистилляции нашёл применение в промышленном производстве высокочистого бериллия.
Дистилляция с направленным затвердеванием конденсата (дистилляция с вытягиванием дистиллята) — дистилляционный процесс в контейнере удлинённой формы c полным расплавлением дистиллируемого вещества и конденсацией пара в твёрдую фазу по мере вытягивания конденсата в холодную область. Процесс разработан теоретически.
В получаемом конденсате возникает неравномерное распределение примесей, и наиболее чистая часть конденсата может быть выделена в качестве продукта. Процесс является дистилляционным аналогом нормальной направленной кристаллизации. Распределение примеси в конденсате описывается уравнением:
где — концентрация примеси в дистилляте на расстоянии от начала, — высота конденсата при полностью испарившемся дистиллируемом материале.
Зонная дистилляция — дистилляционный процесс в контейнере удлинённой формы c расплавлением только верхней части рафинируемого вещества в перемещаемой вниз жидкой зоне, с конденсацией пара в твёрдую фазу по мере выхода конденсата в холодную область. Процесс разработан теоретически.
При движении зонного нагревателя вдоль контейнера сверху вниз в контейнере формируется твёрдый конденсат с неравномерным распределением примесей, и наиболее чистая часть конденсата может быть выделена в качестве продукта. Процесс может быть повторён многократно, для чего конденсат, полученный в предыдущем процессе, должен быть перемещён (без переворота) в нижнюю часть контейнера на место рафинируемого вещества. Неравномерность распределения примесей в конденсате (то есть эффективность очистки) растёт с увеличением числа повторений процесса.
Зонная дистилляция является дистилляционным аналогом зонной перекристаллизации. Распределение примесей в конденсате описывается известными уравнениями зонной перекристаллизации с заданным числом проходов зоны — при замене коэффициента распределения для кристаллизации на коэффициент разделения для дистилляции. Так, после одного прохода зоны
где — концентрация примеси в конденсате на расстоянии от начала конденсата, — длина жидкой зоны.
Эффективность дистилляционной очистки может быть повышена введением в систему основа-примесь добавочного компонента (обычно в концентрации 0,5…10 %), который изменяет относительную летучесть примеси. Разновидностью метода является дистилляция в атмосфере активного вещества, прежде всего — водяного пара.
Применяются и другие специальные приёмы повышения эффективности однократной дистилляции - такие как горячий конденсатор, конденсатор с градиентом температуры, создание на поверхности испаряемой жидкости слоя оксида.
Отмечается, что эффективность применения специальных приёмов дистилляции зависит от величины идеального коэффициента разделения в дистиллируемой двойной системе: она меньше в системах, для которых идеальный коэффициент разделения ближе к единице.