Бактерии
- 1 year ago
- 0
- 0

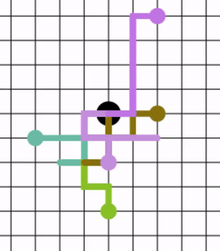
Случайное блуждание — математический объект, известный как стохастический или случайный процесс , который описывает путь, состоящий из последовательности случайных шагов в каком-нибудь математическом пространстве (например, на множестве целых чисел ).
Простейшим примером случайного блуждания является случайное блуждание по числовой прямой целых чисел , , которое начинается в точке 0 и на каждом шаге сдвигается на +1 или на −1 с равной вероятностью . Другими примерами могут послужить траектория движения молекулы в жидкости или газе ( броуновское движение ), поиск пути у животных во время фуражировки , колебания цен акций на фондовом рынке , финансовое состояние игрока : все описанные случаи могут быть аппроксимированы моделями случайного блуждания, даже несмотря на то, что они могут не быть полностью случайными в реальной жизни.
Как видно из примеров, модель случайного блуждания применяется в инженерии и множестве научных областей, включая экологию, психологию, информатику, физику, химию, биологию, экономику и социологию. Случайное блуждание объясняет наблюдаемое поведение многих процессов в этих областях, и, таким образом, служит фундаментальной моделью для зарегистрированной стохастической активности. Так, в математике, значение π может быть приближено с использованием случайного блуждания и агентного моделирования. Понятие случайное блуждание было впервые введено Карлом Пирсоном в 1905 году.
Виды случайных блужданий могут представлять различного рода интерес. Сам термин чаще всего отсылает к особой категории
цепей Маркова
или марковского процесса, а многие зависящие от времени процессы упоминаются как случайные блуждания с модификатором, указывающим на их особые свойства. Случайные блуждания (по Маркову или нет) могут также встречаться в разнообразных областях: обычно изучаемые включают в себя
графы
, числовую прямую
целых
или
действительных
чисел,
векторные пространства
,
кривые
поверхности, многомерные
римановы многообразия
, а также
конечные
, конечнопорожденные группы,
группы Ли
. Параметр времени также может быть различным. В простейшем случае блуждание происходит в дискретном времени и является последовательностью
случайных величин
(
X
t
) = (
X
1 ,
X
2 , ...) , проиндексированных натуральными числами. Однако существуют и случайные блуждания, в которых шаги происходят в произвольный момент времени, и в этом случае позиция
X
t должна быть определена для всех моментов времени
t
∈ [0,+∞) . Особыми случаями случайного блуждания являются полёт Леви и модели
диффузии
, такие как
броуновское движение
.
Случайное блуждание — это фундаментальная тема в обсуждениях марковского процесса, и его математическое изучение очень обширно.
Известной моделью случайного блуждания является блуждание по правильной решётке, где на каждом шаге расположение переходит в другую точку в соответствии с неким распределением вероятностей.
В простом случайном блуждании , расположение может переходить только в соседние точки решётки, формируя путь решётки. В простом симметричном случайном блуждании по локально ограниченной решётке вероятности перехода точки в каждого из её непосредственных соседей равны. Наиболее изученным примером является случайное блуждание по d -мерной решётке целых чисел (иногда называемой гиперкубической решёткой) .
Если пространство состояний ограничено конечным числом измерений, то такая модель случайного блуждания называется простым ограниченным симметричным случайным блужданием , и вероятности переходов зависят от местоположения точки, потому что на пограничных и угловых точках движение ограничено.
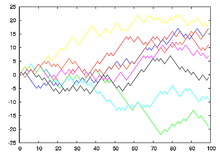
Простейшим примером случайного блуждания является случайное блуждание по числовой прямой целых чисел, , которое начинается в точке 0 и на каждом шаге сдвигается на +1 или на −1 с равной вероятностью.
Это блуждание можно проиллюстрировать следующим образом. Метка ставится на ноль числовой прямой, и подбрасывается «честная» монета. Если выпадает «орёл», метка смещается на одну единицу вправо, а если «решка» — на одну единицу влево. После пяти подкидываний, метка может находиться на −5, −3, −1, 1, 3, 5. За пять подкидываний, среди которых три «орла» и две «решки», идущих в любой последовательности, метка будет на 1. Существуют 10 способов оказаться в точке 1 (путём выпадения трёх «орлов» и двух «решек»), 10 способов оказаться в точке −1 (три «решки» и два «орла»), 5 способов оказаться в точке 3 (четыре «орла» и одна «решка»), 5 способов оказаться в точке −3 (четыре «решки» и один «орёл»), 1 способ оказаться в точке 5 (пять «орлов») и 1 способ оказаться в точке −5 (пять «решек»). Возможные исходы пяти бросков проиллюстрированы ниже.



Чтобы определить это блуждание формально, возьмём независимые случайные переменные , где каждая переменная равна либо 1 либо −1, с вероятностью, равной 50 % для каждого значения, множество и Ряд называют простым случайным блужданием по . Этот ряд (сумма последовательности −1 и 1) означает пройденное расстояние, если каждая часть блуждания имеет длину, равную единице. Математическое ожидание ряда равно нулю. То есть, среднее значение всех бросков монетки с ростом количества бросков, стремится к нулю. Это следует из свойства конечной аддитивности ожидания:
Аналогично рассуждая, используем независимость случайных величин и факт того, что , видим:
Это даёт понять, что , ожидаемая дистанция после перемещения на n шагов, должна быть порядка . В действительности,
Сколько раз случайное блуждание пересечет границу, если есть возможность блуждать бесконечно? Простейшее случайное блуждание по пересечёт каждую точку бесконечное количество раз. Полученный эффект имеет множество названий: феномен пересечения уровня , рекуррентность или задача о разорении игрока . Причина именно такого названия последнего случая заключается в следующем: игрок с конечным количеством денег в рано или поздно проиграет, если будет играть в честную игру против банка с неограниченным количеством денег. Деньги игрока представляют собой случайное блуждание, и в какой-то момент времени оно достигнет нуля и игра будет окончена.
Пусть a и b — положительные целые числа, тогда ожидаемое количество шагов, когда простое одномерное случайное блуждание с началом в точке 0 впервые достигнет b или −a равна ab . Вероятность того, что данное блуждание достигент b прежде, чем достигнет − a , равна , что следует из того факта, что простое случайное блуждание является мартингалом .
Некоторые из упомянутых выше результатов могут быть получены из свойств треугольника Паскаля . Количество всех различных блужданий по n
шагов, где каждый шаг это либо +1, либо −1 равно 2 n . Для простого случайного блуждания каждый из этих шагов равновероятен. Для того, чтобы равнялось числу k , необходимо и достаточно, чтобы число шагов на +1 в блуждани превышало те, что на −1 на число k . Следовательно, шаг на +1 должен встретиться (n + k)/2 раз среди n шагов блуждания, следовательно, количество блужданий, удовлетворяющих условию , равняется количеству способов выбрать (n + k)/2 элементов из n -элементного множества. Это обозначается, как . Чтобы данное выражение имело смысл, необходимо, чтобы сумма n + k была чётным числом, что значит числа n и k одновременно должны быть либо чёнтыми, либо нечётными. Следовательно, вероятность того, что будет равна .Представляя записи треугольника Паскаля с точки зрения факториалов и используя формулу Стирлинга , можно получить хорошие оценки этих вероятностей для больших значений .
Если для краткости ограничить пространство до +, то количество способов, в которых случайное блуждание остановится на каком-то номере после пяти шагов может быть показано как {0,5,0,4,0,1}.
Продемонстрируем это соответствие треугольнику Паскаля для малых значений n . На нулевом шаге, единственная возможность — это остаться в нуле. Однако уже на первом ходу существует возможность оказаться либо в −1, либо в 1. На второй ход, из 1 можно сместиться на точку 2, либо же обратно в нуль. Из −1 можно сдвинуться в −2 или же обратно в нуль. Следовательно, существет один случай, когда мы окажемся в точке −2, два случая, когда в нуле, и один случай — в точке 2.
| k | −5 | −4 | −3 | −2 | −1 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||||
| 1 | 1 | ||||||||||
| 1 | 2 | 1 | |||||||||
| 1 | 3 | 3 | 1 | ||||||||
| 1 | 4 | 6 | 4 | 1 | |||||||
| 1 | 5 | 10 | 10 | 5 | 1 |
Центральная предельная теорема и закон повторного логарифма описывают важные аспекты поведения простого случайного блуждания по . В частности, с увеличением n вероятности (в пропорции с числами в каждой строке) стремятся к нормальному распределению .
Прямым обобщением можно считать случайные блуждания по кристаллическим решёткам (бесконечнократные абелевы покрывающие графы конечныы графов). На самом деле, в таких условиях возможно даже утвердить центральную предельную теорему и теорему о больших уклонениях.
Одномерное дискретное случайное блуждание является цепью Маркова с целыми состояниями, чьё начальное распределение задаётся функцией вероятности случайной величины , а матрица переходных вероятностей имеет вид
то есть

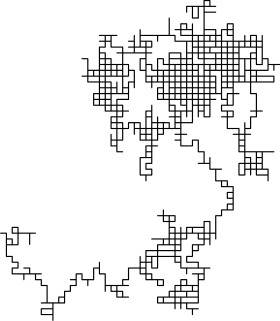
В повышенных размерностях множество точек случайного блуждания имеет довольно интересные геометрические свойства. Фактически, мы получаем дискретный фрактал , то есть множество, которое показывает стохастическое самоподобие при увеличении масштаба. При малом масштабе можно наблюдать «зазубренность» на сетке, по которой осуществляется блуждание. Две книги Лоулера, представленные в ссылках, являются хорошим источником материала по данной теме. Траектория случайного блуждания — это совокупность посещенных точек, рассматриваемых как множество с точностью до момента времени , когда блуждание достигло точки. В одном измерении траектория представляет собой просто все точки между минимальной высотой и максимальной высотой, которое достигло блуждание (обе, в среднем, порядка ).
Для визуализации двухмерного случая, можно представить человека, случайно гуляющего по городу. Этот город фактически бесконечен и расположен в квадратной сетке тротуаров. На каждом перекрестке человек случайным образом выбирает один из четырёх возможных маршрутов (в том числе тот, по которому он пришёл). Формально, это случайное блуждание по множеству всех точек на плоскости с целочисленными координатами .
Вернётся ли когда-нибудь этот человек в начальную точку блуждания? Данный случай это двухмерный эквивалент проблемы пересечения уровня, оговоренной выше. В 1921 Дьёрдь Пойя доказал, что человек почти наверняка вернётся в случае двухмерного случайного блуждания, но для трёх измерений или больше, вероятность возвращения уменьшается с увеличением количества измерений. В трёхмерном случае, вероятность уменьшается примерно до 34 %. Математик Сидзуо Какутани известен своей цитатой касательно такого результата: «Пьяница рано или поздно найдет свой путь домой, а вот пьяная птица может потеряться навсегда».
Ещё один вариант этого вопроса, который также задал Пойя звучит так: если два человека покинут одну стартовую точку, то встретятся ли они когда-нибудь? Можно рассуждать, что разница между их местоположениями (два независимых случайных блуждания) также является простым случайным блужданием, так что они почти наверняка встретятся в двухмерном блуждании, но для трёх измерений или больше, вероятность возвращения так же, как и в предыдущем случае, уменьшается с увеличением количества измерений. Пал Эрдёш и Сэмюэл Джеймс Тейлор также показали в 1960 что для измерений, меньших или равных 4, два независимых случайных блуждания, начиная с любых двух заданных точек, почти наверняка имеют бесконечно много пересечений, но для измерений, превышающих 5, они почти наверняка пересекаются лишь конечное число раз.
Асимптотическая функция для двухмерного случайного блуждания при увеличении числа шагов определяется распределением Рэлея . Распределение вероятностей является функцией радиуса от начала координат, и для каждого шага длина шага постоянна.
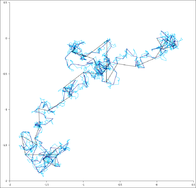
Винеровский процесс — стохастический процесс, который по своему поведению схож с броуновским движением , физическим явлением диффузии мелких частиц в жидкости. (Иногда винеровский процесс называют броуновским движением, хотя, строго говоря, винеровский процесс это модель, а броуновское движение — моделируемое явление.)
Винеровский процесс — это одномерного случайного блуждания. Это значит, что если взять случайное блуждание с очень малыми шагами, то можно будет получить приближение к винеровскому процессу (и, с меньшей точностью, к броуновскому движению). Выражаясь более точно, если длина шага равна ε, необходимо взять блуждание длиной L /ε 2 тобы аппроксимировать винеровский путь L . По мере того, как длина шага стремится к нулю (и количество шагов пропорционально увеличивается), случайное блуждание покрывает винеровский процесс в соответствующем смысле. Формально, если B это пространство всех путей длины L с максимальной топологией, и если M — пространство мер над B с нормальной топологией, тогда конвергенция находится в пространстве M . По аналогии, винеровский процесс в нескольких измерениях это масштабируемый предел случайного блуждания в таком же количестве измерений.
Случайное блуждание это дискретный фрактал (функция с целым числом измерений; 1, 2, …), а траектория винеровского процесса — настоящий фрактал, и между ними двумя существует определённая связь. Например, возьмем случайное блуждание и будем «шагать» до тех пор, пока не пройдем окружность радиуса r, умноженного на длину шага. Тогда среднее количество шагов, необходимое, чтобы совершить блуждание, будет равно r 2 . Этот факт — дискретная версия того факта, что блуждание винеровского процесса это фрактал размерности Хаусдорфа 2.
В двухмерном пространстве, среднее число точек, которые проходит случайное блуждание на границе своей траектории равно r 4/3 . Это соответствует тому факту, что граница траектории винеровского процесса это фрактал размерности 4/3, что было предположено Мандельбротом с помощью использования симуляций, но было доказано только в 2000 году Лоулером, Шраммом и Вернером .
Винеровский процесс имеет много симметрий , в отличие от случайного блуждания. Например, блуждание винеровского процесса инвариантно к вращению, а случайное блуждание — нет, потому что не инвариантна к вращению его сетка (случайное блуждание инвариантно к вращению на 90 градусов, в то время как винеровские процессы инвариантны к вращению, скажем, ещё и на 17 градусов). Это значит, что во многих случаях, задачи, заданные на случайном блуждании, легче решить следующим образом: перенести задачу на винеровский процесс, решить задачу там, а затем перенести обратно. С другой стороны, некоторые задачи проще решить на случайном блуждании, благодаря его дискретной природе.
Сходимость случайного блуждания к винеровскому процессу выполняется с помощью центральной предельной теоремы и теоремы Донскера. Для частицы в известной зафиксированной позиции в t = 0, центральная предельная теорема говорит нам, что после большого количества независимых шагов случайного блуждания, позиция блуждающего будет распределена в соответствии с нормальным распределением дисперсии :
где t — это время, прошедшее с начала случайного блуждания, — это размер шага в блуждании, а — это время, прошедшее между двумя последующими шагами.
Данный случай соответствует функции Грина уравнения диффузии , которое описывает винеровский процесс, что позволяет предположить, что после достаточно большого количества шагов, случайное блуждание сходится к винеровскомому процессу.
В трёхмерном случае, дисперсия, соответствующая функции Грина уравнения диффузии:
Выравнивая эту величину с дисперсией, связанной с положением случайного ходока, можно получить эквивалентный коэффициент диффузии, рассматриваемый для асимптотического винеровского процесса, к которому сходится случайное блуждание после достаточно большого числа шагов:
Замечание: два вышесказанных выражения дисперсии соответствует распределению, связанным с вектором , который соединяет два конца случайного блуждания в трёх измерениях. Разница, связанная с каждым компонентом, , или составляет только одну треть от общего значения (всё ещё 3D).
Для 2D:
Для 1D:
Рассмотрим случайное блуждание , где .
Центральная предельная теорема утверждает, что по распределению при .
Однако для случайных блужданий это утверждение можно значительно усилить.
Построим по случайный процесс , определив его следующим образом: , а при остальных мы доопределим процесс линейным продолжением:
Из центральной предельной теоремы по распределению при
Это означает сходимость одномерных распределений процесса к одномерным распределениям винеровского процесса . Теорема Донскера, называемая также принципом инвариантности, утверждает, что имеет место слабая сходимость процессов,
Слабая сходимость процессов означает сходимость непрерывных по винеровской мере функционалов, то есть позволяет рассчитывать значения функционалов от броуновского движения (например максимума, минимума, последнего нуля, момента первого достижения уровня и других) предельным переходом от простого случайного блуждания.
Случайное блуждание с длиной шага, которая варьируется в зависимости от нормального распределения используется в качестве данных временных рядов реального мира, таких как финансовые рынки. Формула Блэка — Шуолза , например, использует гауссово случайное блуждание как основное предположение.
В данном случае размер шага является обратным кумулятивным нормальным распределением где 0 ≤ z ≤ 1 и является равномерно распределенным случайным числом, а μ и σ это среднее и стандартное отклонения нормального распределения, соответственно.
Если μ ненулевое, случайное блуждание будет зависеть от линейного тренда (англ. linear trend). Если v s это начальное значение случайного блуждания, то ожидаемое значение после n шагов, будет равняться v s + n μ.
Для особого случая, когда μ равно нулю, после n шагов, распределение вероятностей пройденной дистанции определяется, как N (0, n σ 2 ), где N () это обозначение для нормального распределения, n это число шагов, а σ взято из вышесказанного обратного кумулятивного нормального распределения.
Доказательство: гауссово случайное блуждание может быть представлено как сумма последовательности независимых и одинаково распределенных случайных величин, X i из обратного кумулятивного нормального распределения, где среднее значение равно нулю и σ взята из первоначального обратного кумулятивного нормального распределения:
но у нас есть распределение для суммы двух независимых нормально распределенных случайных величин, Z = X + Y, полученных благодаря
В нашем случае, μ X = μ Y = 0 and σ 2 X = σ 2 Y = σ 2 дают:
По индукции, для n шагов имеем:
Для шагов, распределенных в соответствии с любым распределением с нулевым средним и конечной дисперсией (не обязательно только нормальное распределение), среднее квадратическое пройденного после n шагов расстояния определяется, как:
Но для гауссового случайного блуждания это только стандартное отклонение рапределения пройденного после n шагов расстояния. Следовательно, если μ равняется нулю, и если среднее квадратическое преодолённой дистанции равняется одному стандартному отклонению, существует 68,27 % веорятность что среднее квадратическое преодолённой дистанции после n шагов будет находиться между ± σ . Также, существует 50 % вероятность что пройденная дистанция после n шагов будет находиться между ± 0.6745σ .
В неупорядоченных системах, таких как пористые среды и фракталы, может быть пропроциональным не , а . Экспонента называется экспонентой аномальной диффузии и может быть больше или меньше 2. Аномальная диффузия также может быть выражена как σ r 2 ~ Dt α где α — параметр аномалии. Некоторые диффузии в случайной среде даже пропорциональны степени логарифма времени, например блуждание Синая или диффузия Брокса.
Количество различных друг от друга мест, посещённых единственным случайным ходоком , было широко изучено для квадратных и кубических решёток и фракталов. Эта величина полезна для анализа проблем тупиков (англ. trapping ) и кинетических реакций. Она также связана с колебательной плотностью состояний, диффузионными реакциями процессов и распределением популяций в экологии. Обобщение этой задачи на количество отдельных мест, посещенных случайными ходоками, обозначаемое как , недавно было изучено для d -мерных евклидовых решёток. Число различных мест, посещенных N ходоками не просто связано с числом различных мест, посещённых каждым ходоком.
Оценка количества информации случайного блуждания по Гауссу относительно квадрата расстояния ошибки, то есть его квадратичная функция искажения, заданная параметрически:
где . Следовательно, невозможно бинарно закодировать менее чем количеством битов, а затем раскодировать с ожидаемой среднеквадратичной ошибкой меньшей чем . С другой стороны, для любого , существует достаточно большое и двочиный код с не более чем элементами, такой что ожидаемая среднеквадратическая ошибка при восстановлении из этого кода не более .

Как уже упоминалось, диапазон природных явлений, которые попытались описать некоторыми разновидностями случайных блужданий, является значительным. В частности, в физике, химии, материаловедении , биологии и других различных науках. Вот некоторые применения случайного блуждания:
Во всех этих случаях случайное блуждание часто заменяется броуновским движением:
Несколько видов случайных процессов было признано похожими с чистыми случайными блужданиями, но в которых простая структура может быть более обобщенной. Чистая структура может быть охарактеризована шагами, определяемыми независимыми и одинаково распределенными случайными величинами .
Случайное блуждание длины k на, возможно, бесконечном графе G с корнем 0 это стохастический процесс со случайными величинами , такие что , а это вершина, выбранная равномерно-случайно среди соседей . Тогда число — это вероятность, что случайное блуждание длины k начинается в v и заканчивается в w . В частности, если G — это граф с корнем 0 , — это вероятность, что случайное блуждание с шагом вернется в 0 .
По аналогии с ранее описанной секции (повышенные размерности), предположим, что сейчас наш город больше не представляет собой идеальную квадратную сетку. Когда наш человек достигает определённого перекрестка, он с равной вероятностью выбирает между разными доступными дорогами. Таким образом, если на перекрестке семь выходов, человек пойдет к каждому с вероятностью одна седьмая. Таким образом, мы получим случайное блуждание на графе. Доберется ли наш человек до своего дома? Оказывается, при довольно хороших условиях ответ остается положительным, но, в зависимости от графа, на следующий вопрос ('Встретятся ли два человека?') ответ «бесконечно часто» уже может не быть почти достоверным событием.
Примером, когда человек почти наверняка дойдет до дома, является случай, когда длины всех кварталов находятся в диапазоне от a до b (где a и b это два конечных положительных числа). Важно: мы не предполагаем, что граф планарный , то есть в городе могут существовать тоннели и мосты. Один из способов доказать этот результат — подключение к электрическим сетям . Возьмем карту города и поместим резистор сопротивлением 1 Ом на каждый квартал. Теперь измерим «сопротивление между точкой и бесконечностью». Иными словами, выберем какой-нибудь номер R и возьмем все точки в электрической сети с расстоянием между ними и нашей точкой большем, чем R, и соединим их вместе. Получим конечную электрическую сеть, в которой мы можем измерить сопротивление между нашей точкой и другими точками сети. Устремим R к бесконечности. Полученный предел называется сопротивление между точкой и бесконечностью .
Оказывается, что следующее предположение является истинным (элементарное доказательство можно найти в книге Дойла и Снелла):
Теорема : граф является преходящим тогда и только тогда, когда сопротивление между точкой и бесконечностью конечно. Причем, выбор точки неважен, если граф связный.
Иными словами, в преходящей системе, нужно только преодолеть конечное сопротивление, чтобы добраться до бесконечности из любой точки. В рекуррентной системе, сопротивление между любой точкой и бесконечностью бесконечно.
Случайное блуждание по графу это особый случай цепи Маркова . В отличие от общей цепи Маркова, случайное блуждание по графу обладает свойством, называемым временной симметрией или обратимостью . Грубо говоря, это свойство, также называемое принципом детального равновесия , означает, что вероятности пересечения заданного пути в одном или другом направлении имеют очень простую связь между ними (если граф регулярный , то они равны). Данное свойство имеет важные следствия.
Начиная с 1980-х, было проведено много исследований, чтобы связать свойства графа со случайными блужданиями. В добавление к электрической сети, описанной выше, существуют также связи с изопериметрическими неравенствами, функциональными неравенствами, такимим как неравенства и , и со свойствами решений уравнения Лапласа . Значительная часть таких исследований была сосредоточена на графах Кэли конечнопорожденных групп. Во многих случаях эти дискретные результаты переносятся на многообразия и группы Ли или выводятся из них.
Говоря о случайных графах , в частности о модели Эрдёша-Реньи , были получены аналитические результаты некоторых свойств случайных ходоков. Они включают в себя распределение первых и последних попаданий (англ. hitting time) ходока, где первое попадание это первый случай, когда ходок впервые наступает на ранее посещенное место, а последнее совпадает со случаем, когда ходоку некуда больше идти, кроме как на посещенное ранее место.
Хорошей справкой по случайному блужданию на графе является онлайн книга. Для изучения групп подойдут книги Вёсса. Если ядро переходов само по себе является случайным (на основе среды ), то случайное блуждание называется «случайным блужданием в случайной среде». Когда закон случайного блуждания включает в себя случайность , закон называется отожженным (англ. annealed ); с другой стороны, если рассматривается как фиксированное, закон зовётся закаленным (англ. quenched ).
Мы можем выбрать каждое возможное ребро графа с такой же вероятностью, как и локальный максимум неопределенности (энтропии). Мы также можем сделать это глобально — в случайном блуждании с максимальной энтропией (англ. maximal entropy random walk, MERW ) необходимо, чтобы все пути были равновероятны или, иными словами, для любых двух вершин, каждый путь заданной длины равновероятен. Такое блуждание имеет гораздо более сильные локализирующие свойства.
Существует отдельный вид случайных блужданий, в котором каждый шаг неким сложным образом зависит от предыдущего. Они более сложны для аналитического решения, чем обычные случайные блуждания; тем не менее, поведение любой модели случайного ходока можно получить с помощью компьютеров. Например:
Самоизбегающее блуждание длины n на это случайный путь длиной в n шагов, со стартом в начале координат, который проходит только по соседним точкам в и никогда не проходит через одну точку дважды. В двухмерном случае такой путь обычно очень короткий , в то время как в повышенном измерении он растет безгранично. Данная модель часто используется в физике полимеров (с 1960-х).
Долгосрочные коррелирующие временные ряды встречаются во многих биологических, климатологических и экономических системах:
Случайные блуждания, в которых направление движения в один момент времени коррелирует с направлением движения в следующий момент времени. Используется для моделирования передвижений животных.