Ви́ллеброрд Снелл ван Ро́йен ( нидерл. Willebrord Snel van Royen ; 13 июня 1580 , Лейден — 30 октября 1626 , Лейден ) — нидерландский математик , физик и астроном , ученик Людольфа ван Цейлена , профессор Лейденского университета . В части русских источников он именуется Снелль , Снеллий или Снел , печатался под латинизированным именем Снеллиус ( Snellius ).

Труды в области геометрии, тригонометрии, оптики и астрономии. Открыл закон преломления света («закон Снеллиуса»), лежащий в основании современной геометрической оптики . Первым применил триангуляцию для измерения длины земного меридиана , получил хорошую оценку радиуса Земли .

Биография

Родился в Лейдене в семье профессора математики Лейденского университета Рудольфа Снелла (1546—1613), став первым из троих его детей (двое других позднее умерли в детстве). Учился в Лейденском университете .

С 1600 года, вместе с Адрианом ван Роменом , путешествовал по различным европейским странам, в основном обсуждая астрономические проблемы. Проведя некоторое время в Вюрцбурге, два математика отправились в Прагу, где ван Ромен представил Снелла императорскому астроному Тихо Браге и Иоганну Кеплеру . Снелл провёл некоторое время с Браге, помогая ему проводить наблюдения, и, несомненно, он сам многому научился во время этого визита. Однако в октябре 1601 года Браге умер. Впоследствии Кеплер с глубоким уважением отзывался о Снелле (в трактате Stereometria doliorum , 1615) как о «всемирно прославленном геометре» ( лат. geometrarum nostri seculi decus) .

Далее Снелл и ван Ромен поехали в Германию, где общались с Иоганном Преториусом , Михаэлем Мёстлином и другими учёными. Весной 1602 года Снелл ненадолго вернулся в Лейден, затем в 1603 году отправился в Париж, где продолжил изучение права, но также имел много контактов с математиками. После этого визита он бросил изучение права и из Лейдена почти не выезжал .

В 1604 году Снелл стал помогать отцу, здоровье которого ухудшилось, преподавать математику в университете. В этот период Снелл опубликовал комментарии работ Рамуса , а также переводы произведений Стевина и ван Цейлена . В 1608 году защитил диссертацию. В августе 1608 года он женился на Марии де Ланге, дочери бургомистра Схонховена . Из их детей выжили трое .

В 1613 году, после смерти отца, занял его кафедру и, начиная с 1615 года, стал полноправным профессором Лейденского университета .

В 1626 году в возрасте 46 лет Снелл тяжело заболел и спустя две недели умер от некоей «колики», вызвавшей жар и паралич рук и ног. Похоронен 4 ноября в главной церкви Лейдена ( Pieterskerk ). Двадцать студентов несли его гроб .

Научная деятельность

В 1600-е годы Снелл сделал попытку реконструкции утерянных книг Аполлония Пергского (их содержание было кратко передано Паппом Александрийским ). Результаты Снелл опубликовал в 1607—1608 годах; он подготовил реконструкцию ещё одной книги Аполлония, однако она не была опубликована и впоследствии затерялась .

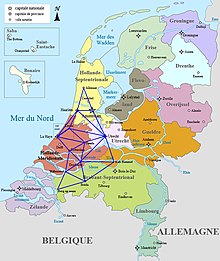
Снелл предложил использовать метод подобия треугольников для проведения геодезических измерений; при помощи этого метода он решил задачу, названную впоследствии « задачей Потенота »: найти точку, из которой стороны данного (плоского) треугольника видны под заданными углами. В своей работе «Eratosthenes Batavus» («Голландский Эратосфен », 1617 год), описывался метод триангуляции , который был открыт его соотечественником Геммой Фризиусом и стал, благодаря поддержке Снелла, широко используемым при съёмке и точном картографировании больших территорий .

В этой работе Снелл попытался измерить окружность Земли, что потребовало значительного количества измерений. Снелл взял за основу расстояние от своего дома до шпиля местной церкви, а затем построил систему треугольников, которая позволила ему определить расстояние между городами Алкмар и Берген-оп-Зомом , которое составляет около 130 км. Он выбрал эти города, поскольку они находились примерно на одном меридиане (по современным данным, Алкмар находится на 4° 45' 0"' восточной долготы и Берген-оп-Зом на 4° 18' 0" восточной долготы). Впервые в Европе Снелл ввёл важное понятие полярного треугольника . Всего в сети из четырнадцати городов было выполнено 53 триангуляционных измерения; основными ориентирами всюду были церковные шпили.

Для точного выполнения измерений Снелл построил большой (210 см) квадрант , с помощью которого он мог измерять углы с точностью до десятых долей градуса. Этот квадрант до сих пор можно увидеть в Музее Бурхаве в Лейдене .

В результате своих расчётов Снелл получил хорошую оценку окружности Земли — в переводе на метрическую систему : 38653 км (ошибка 3,5 %). Снелл посвятил книгу Генеральным штатам , что было мудрым финансовым шагом, поскольку взамен они наградили его суммой, равной почти половине его годового оклада . Снелл собирался расширить сеть городов, охваченных картографированием, но преждевременная смерть не позволила это сделать .

Часть трудов Снелла посвящены проблемам астрономии. Трактат Descriptio Cometae (1619) содержит его собственные наблюдения кометы, появившейся в ноябре 1618 года. В этой работе Снелл резко критиковал Аристотеля и подчёркивал, насколько вредно для развития науки продолжать относиться к его устаревшим взглядам с излишним почтением. Вместе с тем Снелл не принял гелиоцентрическую систему Коперника и твёрдо стоял на геоцентрических позициях.

В 1621 году Снелл описал закон преломления света . Однако ни этот, ни результаты других многочисленных экспериментов по оптике он опубликовать не успел. Исаак Восс в сочинении «Природа света» ( De natura lucis , 1662) сообщил, что сын Виллеброда Снелла показывал ему рукопись сочинения отца, состоявшего из трёх книг; закон преломления там был выражен в следующей форме: «в одних и тех же средах отношение косекансов углов падения и преломления остаётся постоянным» .

Позже закон Снеллиуса был независимо открыт и опубликован Рене Декартом в трактате « Рассуждение о методе » (приложение «Диоптрика», 1637). Приоритет Снелла установил Христиан Гюйгенс в 1703 году, спустя 77 лет после смерти Снелла, когда этот закон уже был общеизвестен . Недоброжелатели обвинили Декарта в плагиате , подозревая, что во время одного из своих визитов в Лейден Декарт услышал об открытии Снелла и смог ознакомиться с его рукописями . Однако никаких доказательств плагиата нет, а самостоятельный путь Декарта к этому открытию подробно изучен историками .

В книге « Cyclometricus » (1621) Снелл приводит значение числа ${\displaystyle \pi }$ с 35 десятичными знаками. Для вычислений он использовал двойное неравенство :

${\displaystyle {\frac {3\sin x}{2+\cos x}}<x<\operatorname {tg} {\frac {x}{3}}+2\sin {\frac {x}{3}}}$

Первое из этих неравенств было знакомо уже в средние века Николаю Кузанскому .

В труде « Tiphys batavus » (1624), посвящённом актуальным для Нидерландов проблемам мореплавания, Снелл исследовал важную в теории навигации и картографии кривую на сфере, пересекающую все меридианы под постоянным углом. Он назвал её « локсодромой ». Работа состояла из двух частей, одна из которых была теоретической, а другая посвящена практическим приложениям .

В изданном посмертно труде 1627 года Снелл внёс вклад в тригонометрию. В частности, впервые приведена формула для вычисления площади треугольника , когда известны длины двух сторон и угол между ними : ${\displaystyle S={\frac {1}{2}}ab\cdot \sin \gamma }$ .

Память

В 1935 году Международный астрономический союз присвоил имя «Снеллиус» кратеру на видимой стороне Луны .

В честь учёного названы также:

• «Медаль Снеллиуса», присуждаемая Обществом содействия физике, медицине и хирургии ( нидерл. Genootschap ter Bevordering van Natuur-, Genees- en Heelkunde) за работу в области естественных наук или математики, за исключением химии и биологии. Медаль учреждена в 1951 году и вручается раз в 10 лет .
• Антарктический « » .
• Одно за другим, три исследовательских корабля Королевских военно-морских сил Нидерландов (в 1929, 1952 и 2003 годах), последнее из них продолжает находиться в строю .

Труды

• 
  Eratosthenes Batavus (1617)
• 
  Cyclometricus (1621)
• 
  Tiphys Batavus (1624)

• Apollonius batavus (Leiden, 1608)
• De re numeraria (Leiden, 1613)
• : [ лат. ] . — Lugduni Batavorum : Joost van Colster, Joris Abrahamsz van der Marsce, 1617.
• : [ лат. ] . — Lugduni Batauorum : Joost van Colster, 1618.
• Descriptio cometae qui anno 1618 mense Novembri primum efjidsit (Leiden, 1619)
• : [ лат. ] . — Lugduni Batavorum : Matthijs Elzevier, Bonaventura Elzevier, 1621.
• Tiphys batavus (Leiden, 1624)
• Canon triangulorum (Leiden, 1626)
• : [ лат. ] . — Lugduni Batavorum : Joannes Maire, 1627. Не закончена, издана посмертно, с дополнениями ученика Снелла Мартинуса Гортензиуса.

Участие как редактора:

• Petiias Ramus , Arithmetica. W. Snellius ed. (Leiden, 1613)
• Вильгельм IV (ландграф Гессен-Касселя) . Coeli et siderum in eo errantium observationes Hassiacae, 1618.
• P. Rami . Meetkonst. Translated by Dirk Houtman, annotations by W. Snel (Amsterdam, 1622)

Примечания

Литература

• Боголюбов А. Н. Снеллиус (Снелль ван Ройен) Виллеброрд // Математики. Механики. Биографический справочник. — Киев: Наукова думка, 1983. — 639 с.
• Вилейтнер Г. История математики от Декарта до середины XIX столетия. — М. : ГИФМЛ, 1960. — 468 с.
• Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича , в трёх томах. — М. : Наука, 1970. — Т. II.
• Храмов Ю. А. Снеллиус Виллеброрд (Snellius, Snell van Royen Villebrord) // Физики : Биографический справочник / Под ред. А. И. Ахиезера . — Изд. 2-е, испр. и доп. — М. : Наука , 1983. — 400 с. — 200 000 экз.

Ссылки

• Джон Дж. О’Коннор и Эдмунд Ф. Робертсон . (англ.) — биография в архиве MacTutor .
• (нидерл.) . Дата обращения: 22 июля 2021.
• (англ.) . Дата обращения: 22 июля 2021.