Колебательный контур — электрическая цепь , содержащая катушку индуктивности , конденсатор и источник электрической энергии. При последовательном соединении элементов цепи колебательный контур называется последовательным, при параллельном — параллельным .

Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания (при отсутствии в ней источника электрической энергии).

Резонансная частота контура определяется так называемой формулой Томсона :

${\displaystyle f_{0}={1 \over 2\pi {\sqrt {LC}}}.}$

Принцип действия

Пусть конденсатор ёмкостью C заряжен до напряжения ${\displaystyle U_{0}}$ . Энергия , запасённая в конденсаторе, составляет

${\displaystyle E_{C}={\frac {CU_{0}^{2}}{2}}.}$

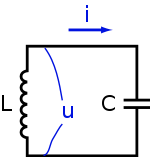
При соединении конденсатора с катушкой индуктивности в цепи потечёт ток ${\displaystyle I}$ , что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции , направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности), в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.

Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора ${\displaystyle E_{C}=0}$ . Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна

${\displaystyle E_{L}={\frac {LI_{0}^{2}}{2}},}$

где ${\displaystyle L}$ — индуктивность катушки, ${\displaystyle I_{0}}$ — максимальное значение тока.

После этого начнётся перезарядка конденсатора, то есть зарядка конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор в этом случае снова будет заряжен до напряжения ${\displaystyle -U_{0}}$ .

В результате в цепи возникают колебания , длительность которых будет обратно пропорциональна потерям энергии в контуре.

Описанные выше процессы в параллельном колебательном контуре называются резонанс токов , что означает, что через индуктивность и ёмкость протекают токи больше тока, проходящего через весь контур, причём эти токи больше в определённое число раз, которое называется добротностью . Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Стоит также заметить, что сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности (в отличие от последовательного колебательного контура, сопротивление которого на резонансной частоте стремится к нулю), а это делает его незаменимым фильтром.

Стоит заметить, что помимо простого колебательного контура, есть ещё колебательные контуры первого, второго и третьего рода, что учитывают потери и имеют другие особенности.

Математическое описание процессов

Напряжение на идеальной катушке индуктивности при изменении протекающего тока:

${\displaystyle u_{L}=L{\frac {di_{L}}{dt}}.}$

Ток, протекающий через идеальный конденсатор, при изменении напряжения на нём:

${\displaystyle i_{C}=C{\frac {du_{C}}{dt}}.}$

Из правил Кирхгофа , для цепи, составленной из параллельно соединённых конденсатора и катушки, следует:

${\displaystyle u_{L}+u_{C}=0,}$ — для напряжений,

и

${\displaystyle i_{C}=i_{L}}$ — для токов.

Совместно решая систему дифференциальных уравнений ( дифференцируя одно из уравнений и подставляя результат в другое), получаем:

${\displaystyle {\frac {d^{2}i(t)}{dt^{2}}}+{\frac {1}{LC}}i(t)=0.}$

Это дифференциальное уравнение гармонического осциллятора с циклической частотой собственных колебаний ${\displaystyle \omega ={\frac {1}{\sqrt {LC}}}}$ (она называется собственной частотой гармонического осциллятора).

Решением этого уравнения 2-го порядка является выражение, зависящее от двух начальных условий:

${\displaystyle i(t)=I_{a}\sin({\omega }t+\varphi),}$

где ${\displaystyle I_{a}}$ — некая постоянная, определяемая начальными условиями, называемая амплитудой колебаний , ${\displaystyle \varphi }$ — также некоторая постоянная, зависящая от начальных условий, называемая начальной фазой .

Например, при начальных условиях ${\displaystyle \varphi =0}$ и амплитуде начального тока ${\displaystyle I_{a}}$ решение сведётся к:

${\displaystyle i(t)=I_{a}\sin({\omega }t).}$

Решение может быть записано также в виде

${\displaystyle i(t)=I_{a1}\sin({\omega }t)+I_{a2}\cos({\omega }t),}$

где ${\displaystyle I_{a1}}$ и ${\displaystyle I_{a2}}$ — некоторые константы, которые связаны с амплитудой ${\displaystyle I_{a}}$ и фазой ${\displaystyle \varphi }$ следующими тригонометрическими соотношениями:

${\displaystyle I_{a1}=I_{a}\cos {(\varphi)},}$

${\displaystyle I_{a2}=I_{a}\sin {(\varphi)}.}$

Комплексное сопротивление ( импеданс ) колебательного контура

Колебательный контур может быть рассмотрен как двухполюсник , представляющий собой параллельное включение конденсатора и катушки индуктивности. Комплексное сопротивление такого двухполюсника можно записать как

${\displaystyle {\hat {z}}(i\omega)\;={\frac {i\omega L}{1-\omega ^{2}LC}},}$

где i — мнимая единица .

Для такого двухполюсника может быть определена т. н. характеристическая частота (или резонансная частота), когда импеданс колебательного контура стремится к бесконечности (знаменатель дроби стремится к нулю).

Эта частота равна

${\displaystyle \omega _{h}={\frac {1}{\sqrt {LC}}}}$

и совпадает по значению с собственной частотой колебательного контура.

Из этого уравнения следует, что на одной и той же частоте может работать множество контуров с разными величинами L и C, но с одинаковым произведением LC. Однако выбор соотношения между L и C зачастую не бывает полностью произвольным, так как обуславливается требуемым значением добротности контура.

Для последовательного контура добротность растёт с увеличением L:

${\displaystyle Q={\frac {1}{R}}{\sqrt {\frac {L}{C}}},}$

где R — активное сопротивление контура. Для параллельного контура:

${\displaystyle Q=R_{e}{\sqrt {\frac {C}{L}}},}$

где ${\displaystyle R_{e}={\frac {L}{CR_{L+C}}}}$ , ( ${\displaystyle R_{L+C}}$ — сумма активных сопротивлений в цепи катушки и цепи конденсатора ).

Понятие добротности связано с тем, что в реальном контуре существуют потери энергии (на излучение и нагрев проводников). Обычно считают, что все потери сосредоточены в некотором эквивалентном сопротивлении ${\displaystyle R_{e}}$ , которое в последовательном контуре включено последовательно с L и C, а в параллельном — параллельно им. Малые потери (то есть высокая добротность) означают, что ${\displaystyle R_{e}}$ в последовательном контуре мало, а в параллельном — велико. В низкочастотном последовательном контуре ${\displaystyle R_{e}}$ легко обретает физический смысл — это в основном активное сопротивление провода катушки и проводников цепи.

Практическое применение

Резонансные контуры широко используются как полосовые и режекторные фильтры — в усилителях , радиоприёмниках , а также в различных устройствах автоматики. Например, на самолётах Ил-62М , Ил-76 и Ту-154М установлены блоки регулирования частоты БРЧ-62БМ, в главном элементе которых — блоке измерения частоты БИЧ-1 — имеются два колебательных контура, настроенных на частоты 760 и 840 Гц. На них поступает напряжение с номинальной частотой 800 Гц от подвозбудителя генератора (сам генератор при этом выдаёт 400 Гц). При отклонении частоты от номинальной реактивное сопротивление одного из контуров становится больше, чем другого, и БРЧ выдаёт на привод постоянных оборотов генератора управляющий сигнал для коррекции оборотов генератора. Если частота поднялась выше номинальной — сопротивление второго контура станет меньше, чем первого, и БРЧ выдаст сигнал на уменьшение оборотов генератора, если частота упала — то наоборот. Так поддерживается постоянство частоты напряжения генератора при изменении оборотов двигателя .

См. также

• Резонанс токов
• Резонанс напряжений
• Электрический импеданс
• Многополюсник
• Электромагнитное излучение
• Потенциальная энергия
• Кинетическая энергия
• RC-цепь
• LR-цепь
• Гетеродинный индикатор резонанса

Примечания

Литература

• Попов В. П. Основы теории цепей: Учеб. для вузов / В. П. Попов. — 4-е изд., испр. — М.: Высш. шк., 2003. — 575 с.
• Скрипников Ю. Ф. Колебательный контур — М.: Энергия, 1970—128 с.: ил. — (МРБ; Вып. 739)
• Изюмов Н. М., Линде Д. П. Основы радиотехники. — М.:Радио и связь, 1983
• Фролов А. Д. Радиодетали и узлы. — М. : Высшая школа, 1975. — С. 195-223. — 440 с. — (Учебное пособие для вузов).