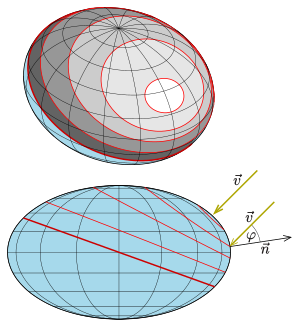
Изофота ( англ. Isophote) — кривая на освещённой поверхности, соединяющая точки с одинаковой яркостью . Предположим, что освещённость создаётся пучком параллельных лучей света, а яркость ${\displaystyle b}$ выражается скалярным произведением :

${\displaystyle b(P)={\vec {n}}(P)\cdot {\vec {v}}=\cos \varphi \ .}$

${\displaystyle {\vec {n}}(P)}$ представляет собой единичный вектор , нормальный к поверхности в точке ${\displaystyle P}$ , а вектор ${\displaystyle {\vec {v}}}$ является единичным вектором в направлении распространения света. В случае ${\displaystyle b(P)=0}$ , когда свет перпендикулярен к нормали к поверхности, точка ${\displaystyle P}$ является точкой на силуэте поверхности в направлении ${\displaystyle {\vec {v}}}$ . Яркость 1 означает, что луч света перпендикулярен поверхности. На плоскости в рамках предположения о параллельности пучка лучей изофоты будут отсутствовать.

Применение

В системах автоматизированного проектирования изофоты используются для оптического контроля гладкости стыковки поверхностей. Для поверхности (заданной неявно или параметрически), дифференцируемой достаточное количество раз, вектор нормали зависит от первых производных. Следовательно, дифференцируемость изофот и их геометрическая непрерывность имеют на 1 меньший порядок, чем сама поверхность. Если в точке поверхности непрерывными являются только касательные плоскости (гладкость порядка 1), то изофоты обладают изломами (гладкость только нулевого порядка).

В следующем примере две пересекающиеся поверхности Безье закрыты участком третьей поверхности. На рисунке слева закрывающая поверхность касается поверхностей Безье с порядком гладкости 1, на рисунке справа — с порядком гладкости 2. Из самих рисунков разница ситуаций видна плохо, но исследование геометрической непрерывности изофот показывает: на рисунке слева изофоты имеют изломы (гладкость порядка 0), а на рисунке справа изофоты выглядят гладкими (гладкость порядка 1).

В астрономии

В астрономии изофотой называют кривую на изображении объекта, проходящую через точки с одинаковой поверхностной яркостью . Часто их применяют для графического представления распределения поверхностной яркости в протяжённых источниках света, например, в галактиках . В отличие от простых изображений, карты изофот позволяют одновременно визуально оценить структуру галактики как в центральных областях, так и на периферии, а также приближённо оценить закон, по которому распределена поверхностная яркость в галактике .

Определение точек изофоты

на неявно заданной поверхности

Для неявно заданной поверхности с уравнением ${\displaystyle f(x,y,z)=0}$ изофоты удовлетворяют равенству

${\displaystyle {\frac {\nabla f\cdot {\vec {v}}}{|\nabla f|}}=c\ .}$

Это означает: точки на изофоте с заданным параметром ${\displaystyle c}$ представляют собой решение нелинейной системы

• ${\displaystyle \ f(x,y,z)=0,\qquad \nabla f(x,y,z)\cdot {\vec {v}}-c\;|\nabla f(x,y,z)|=0\ ,}$

которую можно рассматривать как линию пересечения двух неявно заданных поверхностей. Используя алгоритм, представленный Bajaj и др. (см. ссылки), можно вычислить многоугольник из точек изофот.

на параметрически заданной поверхности

В случае параметрически заданной поверхности ${\displaystyle {\vec {x}}={\vec {S}}(s,t)}$ уравнение для изофот имеет вид

${\displaystyle {\frac {({\vec {S}}_{s}\times {\vec {S}}_{t})\cdot {\vec {v}}}{|{\vec {S}}_{s}\times {\vec {S}}_{t}|}}=c\ ,}$

что эквивалентно выражению

• ${\displaystyle \ ({\vec {S}}_{s}\times {\vec {S}}_{t})\cdot {\vec {v}}-c\;|{\vec {S}}_{s}\times {\vec {S}}_{t}|=0\ .}$

Данное уравнение описывает неявно заданную кривую в плоскости s-t, которую можно представить с помощью подходящего алгоритма и преобразовать с помощью ${\displaystyle {\vec {S}}(s,t)}$ в точки на поверхности.

Литература

• J. Hoschek, D. Lasser: Grundlagen der geometrischen Datenverarbeitung , Teubner-Verlag, Stuttgart, 1989, ISBN 3-519-02962-6 , p. 31.
• Z. Sun, S. Shan, H. Sang et. al.: Biometric Recognition , Springer, 2014, ISBN 978-3-319-12483-4 , p. 158.
• C.L. Bajaj, C.M. Hoffmann, R.E. Lynch, J.E.H. Hopcroft: Tracing Surface Intersections , (1988) Comp. Aided Geom. Design 5, pp. 285–307.
• C. T. Leondes: Computer Aided and Integrated Manufacturing Systems: Optimization methods , Vol. 3, World Scientific, 2003, ISBN 981-238-981-4 , p. 209.

Примечания

Ссылки