Общая теория относительности
· Математическая формулировка Предсказания
Фундаментальные принципы Специальная теория относительности · Пространство-время · Принцип эквивалентности · Мировая линия · Псевдориманово многообразие
Явления Задача Кеплера в ОТО · · Гравитационная волна · Увлечение инерциальных систем отсчёта Горизонт событий Гравитационная сингулярность Чёрная дыра · Белая дыра Космологическая сингулярность Гравитомагнетизм
Уравнения Уравнения Эйнштейна · Космологическая постоянная · · Постньютоновский формализм
Развитие теории Параметризованный постньютоновский формализм · Теории типа Калуцы — Клейна · Квантовая гравитация · Альтернативные теории
Решения Точные решения: Шварцшильда · Райсснера — Нордстрёма · Керра · Керра — Ньюмена · Гёделя · · Фридмана — Леметра — Робертсона — Уокера Приближённые решения: Постньютоновский формализм · · Численная относительность
Журналы General Relativity and Gravitation · Classical and Quantum Gravity · · Living Reviews in Relativity
Связанные темы Гравитация · Золотой век ОТО
См. также: Портал:Физика

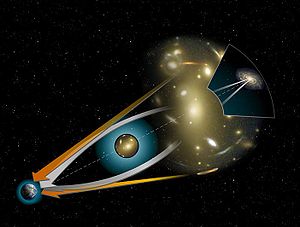
Гравитацио́нная ли́нза — массивное тело ( планета , звезда , галактика , скопление галактик , скопление тёмной материи ), изменяющее своим гравитационным полем направление распространения электромагнитного излучения, подобно тому как обычная линза изменяет направление светового луча. Само явление искривления светового луча под воздействием гравитации было предсказано общей теорией относительности (ОТО) А. Эйнштейна , и обнаружение гравитационных линз явилось одним из подтверждений ОТО .

Как правило, гравитационные линзы, способные существенно исказить изображение фонового объекта, представляют собой достаточно большие сосредоточения массы: галактики и скопления галактик. Более компактные объекты — например, звёзды — тоже отклоняют лучи света, однако на столь малые углы, что зафиксировать такое отклонение в большинстве случаев не представляется возможным. В этом случае можно обычно лишь заметить кратковременное увеличение яркости объекта-линзы в тот момент, когда линза пройдёт между Землёй и фоновым объектом. Если объект-линза яркий, то заметить такое изменение практически невозможно. Если же объект-линза не яркий или же не виден совсем, то такая кратковременная вспышка вполне может наблюдаться. События такого типа называются микролинзированием . Интерес здесь связан не с самим процессом линзирования, а с тем, что он позволяет обнаружить массивные и не видимые никаким иным способом скопления материи.

Ещё одним направлением исследований микролинзирования стала идея использования каустик для получения информации как о самом объекте-линзе, так и о том источнике, чей свет она фокусирует. Подавляющее большинство событий микролинзирования вполне вписывается в предположение, что оба тела сферической формы. Однако в 2—3 % всех случаев наблюдается сложная кривая яркости, с дополнительными короткими пиками, которая свидетельствует о формировании каустик в линзированных изображениях . Такая ситуация может иметь место, если линза имеет неправильную форму, например, если она состоит из двух или более тёмных массивных тел. Наблюдение таких событий безусловно интересно для изучения природы тёмных компактных объектов. Примером успешного определения параметров двойной линзы с помощью изучения каустик может служить случай микролинзирования OGLE-2002-BLG-069 . Кроме того, имеются предложения по использованию каустического микролинзирования для выяснения геометрической формы источника, либо для изучения профиля яркости протяжённого фонового объекта, и в частности для изучения атмосфер звёзд-гигантов.

Наблюдения

Описание

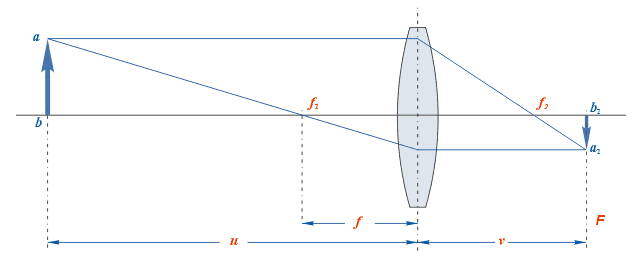
В отличие от оптической линзы , гравитационная линза более всего искривляет свет, проходящий ближе всего к её центру, и менее всего искривляет тот свет, который проходит дальше всего от центра. Следовательно, гравитационная линза не имеет точки фокусировки , однако обладает фокальной линией. Термин «линза», подразумевающий отклонение света из-за гравитации, впервые был использован Оливером Лоджем, который отметил, что «недопустимо говорить, что гравитационное поле Солнца действует как линза, поскольку у него нет фокусного расстояния » . Если источник света, массивный линзирующий объект и наблюдатель расположены на одной прямой, источник света будет виден как кольцо вокруг массивного объекта. При отклонении взаимного расположения тел от прямой наблюдатель сможет увидеть только участок дуги. Впервые это явление было упомянуто физиком из Ленинграда Орестом Даниловичем Хвольсоном в 1924 г. , а численные оценки были проведены Альбертом Эйнштейном в 1936 году . В литературе данный эффект обычно называется кольцом Эйнштейна , так как Хвольсон не стал вычислять ни яркость, ни радиус видимого кольца. В более общем случае, когда эффект гравитационного линзирования вызван системой тел (группой или скоплением галактик ), не обладающей сферической симметрией, источник света будет виден наблюдателю как части дуг, расположенных вокруг линзы. Наблюдатель в таком случае сможет видеть искривлённые размноженные изображения одного и того же объекта. Их количество и форма зависит от взаимного расположения источника света (объекта), линзы и наблюдателя, а также от формы гравитационной потенциальной ямы , создаваемой линзирующим объектом .

Существует три класса гравитационных линз :

1. , вызывающее легко различимые искажения, такие как эйнштейновское кольцо, дуги и размноженные изображения.
2. , вызывающее лишь малые искажения в изображении объекта, который находится позади линзы (далее — объект фона). Эти искажения могут быть зафиксированы только после статистического анализа большого количества объектов фона, что позволяет найти небольшое согласованное искажение их изображений. Линзирование проявляется в небольшом растяжении изображения перпендикулярно направлению к центру линзы. Изучая форму и ориентацию большого количества отдалённых галактик фона, мы получаем возможность измерить линзирующее поле в любой области. Эти данные, в свою очередь, могут быть использованы, чтобы восстановить распределение масс в данной области пространства; в частности, этим методом можно исследовать распределение тёмной материи . Поскольку галактики сами по себе обладают эллиптической формой и искажения от слабого линзирования малы, для использования этого метода необходимо наблюдение большого числа галактик фона. Такого рода обзоры должны тщательно учитывать многие источники систематической погрешности : собственную форму галактик, пространственную функцию отклика светочувствительной матрицы, атмосферные искажения и т. д. Результаты этих исследований важны для оценки космологических параметров, для лучшего понимания и развития модели Лямбда-CDM , а также для того, чтобы обеспечить проверку непротиворечивости с другими космологическими наблюдениями .
3. Микролинзирование не вызывает никакого наблюдаемого искажения формы, но количество света, принимаемое наблюдателем от объекта фона, временно увеличивается. Линзирующим объектом могут быть звёзды Млечного Пути , их планеты, а источником света — звёзды отдалённых галактик или квазары , находящиеся на ещё более далёком расстоянии. В отличие от первых двух случаев, изменение наблюдаемой картины при микролинзировании происходит за характерное время от секунд до сотен дней. Микролинзирование позволяет оценить количество слабосветящихся объектов с массами порядка звёздных (например, белых карликов ) в Галактике, которые могут вносить некоторый вклад в барионную компоненту тёмной материи. Кроме того, микролинзирование является одним из методов поиска экзопланет .

Гравитационное линзирование действует одинаково на все виды электромагнитного излучения , не только на видимый свет. Помимо вышеописанных обзоров галактик, слабое линзирование может изучаться по его влиянию на космическое микроволновое фоновое излучение . Сильное линзирование наблюдалось в радио- и рентгеновском диапазонах.

В случае сильного гравитационного линзирования, если наблюдается несколько изображений объекта фона, то свет от источника, идущий разными путями, будет приходить к наблюдателю в разное время; измерение этой задержки (например, от фонового квазара с переменной яркостью) позволяет оценить распределение масс вдоль луча зрения.

Поиск гравитационных линз

В прошлом большинство гравитационных линз было найдено случайно. Поиск гравитационных линз в северном полушарии (Cosmic Lens All Sky Survey, CLASS), который проводили при помощи радиотелескопа Very Large Array в Нью-Мексико, позволил обнаружить 22 новые линзирующие системы. Это открыло совершенно новые пути исследования от поиска очень далёких объектов до определения величин космологических параметров для лучшего понимания вселенной. ^{[ источник не указан 2334 дня ]}

Подобное исследование из южного полушария позволило бы нам сделать большой шаг к завершению исследований из северного полушария, а также к выявлению новых объектов для изучения. Если такое исследование будет проведено при помощи хорошо откалиброванных и хорошо настроенных инструментов, то можно ожидать результатов, подобным тем, которые были получены в ходе исследования из северного полушария. Примером подходящих данных являются данные, полученные с помощью австралийского телескопа AT20G на базе радиоинтерферометра АТКА. Так как данные были получены с помощью прибора, измеряющего точные данные, похожего на тот, который использовали в северном полушарии, стоит ожидать хороших результатов исследования. AT20G работает на частоте до 20 ГГц в радио полях электромагнитного спектра. Так как используется высокая частота, шансы найти гравитационные линзы вырастают, ведь повышается количество малых базовых объектов (например, квазаров). Это важно, так как проще обнаружить линзу на примере более простых объектов. Этот поиск включает в себя использование интерференционных методов определения примеров и наблюдение за ними в более высоком разрешении. Полное описание проекта сейчас готовится к публикации. ^{[ источник не указан 2334 дня ]}

Астрономы из общества научных исследований имени Макса Планка обнаружили самую отдалённую на тот момент галактику с эффектом гравитационного линзирования (J1000+0221) с помощью телескопа «Хаббл» НАСА . На данный момент эта галактика остаётся самой отдалённой, разделяющей изображение на четыре. Однако международной командой астрономов с помощью телескопа «Хаббл» и телескопа обсерватории Кека была обнаружена спектроскопическими методами ещё более отдалённая галактика, раздваивающая изображение. Открытие и анализ линзы IRC 0218 были опубликованы в Astrophysical Journal Letters 23 июня 2014 г. ^{[ источник не указан 2334 дня ]}

Теория

Гравитационную линзу можно рассматривать как обычную линзу, но только с коэффициентом преломления, зависящим от положения. Тогда общее уравнение для всех моделей можно записать следующим образом :

${\displaystyle \eta ={\frac {D_{s}}{D_{d}}}\xi -D_{ds}{\hat {\alpha }}(\xi)}$

где η — координата источника, ξ — расстояние от центра линзы до точки преломления ( прицельный параметр ) в плоскости линзы, D _s , D _d — расстояния от наблюдателя до источника и линзы соответственно, D _ds — расстояние между линзой и источником, α — угол отклонения, вычисляемый по формуле:

${\displaystyle \alpha ={\frac {4G}{c}}\int _{R^{2}}{\frac {(\xi _{i}-\xi ')\Sigma (\xi)}{|\xi _{i}-\xi '|^{2}}},}$

где Σ — поверхностная плотность, вдоль которой «скользит» луч. Если обозначить характерную длину в плоскости линзы ξ ₀ , а соответствующую ей величину в плоскости источника η ₀ = ξ ₀ D _s / D _l и ввести соответствующие безразмерные векторы x = ξ/ξ ₀ и y = η/η ₀ , то уравнение линзы можно записать в следующем виде:

${\displaystyle y=x-\bigtriangledown \psi (x)=\bigtriangledown \left({\frac {1}{2}}x^{2}-\psi (x)\right)}$

Тогда, если ввести функцию ${\displaystyle \phi (x,y)={\frac {(x-y)^{2}}{2}}-\psi (x),}$ называемую потенциалом Ферма, то можно записать уравнение следующим образом :

${\displaystyle \bigtriangledown \phi (x,y)=0.}$

Временну́ю задержку между изображениями также принято записывать через потенциал Ферма :

${\displaystyle T(x,y)={\frac {1}{c}}\xi _{0}^{2}{\frac {D_{s}}{D_{l}D_{ls}}}(1+z_{l})|\phi (x_{i},y)-\phi (x_{j},y)|}$

Иногда удобно выбрать масштаб ξ ₀ = D _l , тогда x и y — это угловое положение изображения и источника соответственно.

Примечания

Литература

• Захаров А. Ф. Гравитационные линзы и микролинзы. — М. : Янус-К, 1997. — ISBN 5-88929-037-1 .
• Чернин А. Д. // Квант. — 1988. — № 7 . — С. 15—22 .
• Сурдин В. Г. // Энциклопедия КРУГОСВЕТ.
• Blandford & Narayan; Narayan, R. Cosmological applications of gravitational lensing (англ.) // (англ.) (. — 1992. — Vol. 30 , no. 1 . — P. 311—358 . — doi : . — Bibcode : .
• Matthias Bartelmann; Peter Schneider. . — 2000. — 17 августа. 26 февраля 2007 года.
• Khavinson, Dmitry; Neumann, Genevra. (англ.) // Notices of the AMS : journal. — Vol. 55 , no. 6 . — P. 666—675 . .
• Petters, Arlie O.; Levine, Harold; Wambsganss, Joachim. (англ.) . — (англ.) (, 2001. — Vol. 21. — (Progress in Mathematical Physics).

Ссылки

• // Астронет
• Черепащук А. М .
• Chwolson, O. Über eine mögliche Form fiktiver Doppelsterne (англ.) // Astronomische Nachrichten : journal. — Wiley-VCH , 1924. — Vol. 221 , no. 20 . — P. 329—330 . — doi : . — Bibcode : .
• Einstein, Albert . (англ.) // Science : journal. — 1936. — Vol. 84 , no. 2188 . — P. 506—507 . — doi : . — Bibcode : . — . — JSTOR .
• Renn, Jürgen; Tilman Sauer; John Stachel. The Origin of Gravitational Lensing: A Postscript to Einstein's 1936 Science paper (англ.) // Science : journal. — 1997. — Vol. 275 , no. 5297 . — P. 184—186 . — doi : . — Bibcode : . — .