Теория линейных стационарных систем — раздел теории динамических систем , изучающий поведение и динамические свойства линейных стационарных систем (ЛСС). Используется для изучения процессов управления техническими системами, для цифровой обработки сигналов и в других областях науки и техники.

Обзор

Определяющими свойствами для любой линейной стационарной системы являются линейность и стационарность :

• Линейность означает линейную связь между входом и выходом системы.

Формально, линейной называется система, обладающая следующим свойством:

если сигнал на входе системы можно представить взвешенной суммой воздействий (например, двух) —

x ( t ) = A · x ₁ ( t ) + B · x ₂ ( t )

то сигнал на выходе системы является также взвешенной суммой реакций на каждое из воздействий —

y ( t ) = A · y ₁ ( t ) + B · y ₂ ( t )

для любых постоянных A и B .

• Стационарность — означает, что выходной сигнал системы как реакция на любой заданный входной сигнал одинаков для любого момента приложения входного сигнала (с точностью до времени запаздывания момента приложения входного сигнала). В более узком смысле — при запаздывании входного сигнала по времени на некоторую величину, выходной сигнал будет запаздывать на ту же самую величину.

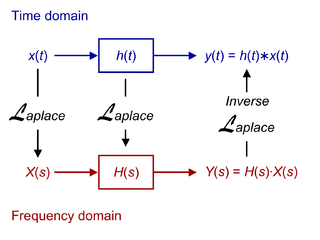
Динамика систем, обладающих вышеперечисленными свойствами, может описываться одной простой функцией, к примеру, импульсной переходной функцией . Выход системы может рассчитываться как свёртка входного сигнала с импульсной переходной функцией системы. Этот метод анализа иногда называется анализом во временной области . Сказанное справедливо и для дискретных систем.

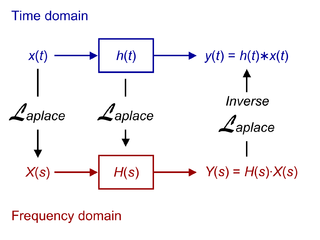
Кроме того, любая ЛСС может быть описана в с помощью своей передаточной функции , которая является преобразованием Лапласа импульсной переходной функции (или Z-преобразованием в случае дискретных систем). В силу свойств этих преобразований, выход системы в частотной области будет равен произведению передаточной функции и соответствующего преобразования входного сигнала. Другими словами, свёртке во временной области соответствует умножение в частотной области.

Для всех ЛСС собственные функции являются комплексными экспонентами . То есть, если вход системы представляет собой комплексный сигнал ${\displaystyle A\exp({st})}$ с некоторой комплексной амплитудой ${\displaystyle A}$ и частотой ${\displaystyle s}$ , то выход будет равен некоторому сигналу ${\displaystyle B\exp({st})}$ с комплексной амплитудой ${\displaystyle B}$ . Отношение ${\displaystyle B/A}$ будет являться передаточной функцией системы на частоте ${\displaystyle s}$ .

Так как синусоиды представляют собой сумму комплексных экспонент с комплексно-сопряжёнными частотами, если вход системы — синусоида, то выходом системы будет также синусоида, в общем случае с другой амплитудой и фазой, но с той же частотой .

Теория ЛСС хорошо подходит для описания многих систем. Большинство ЛСС гораздо проще анализировать, чем нестационарные и нелинейные системы. Любая система, динамика которой описывается линейным дифференциальным уравнением с постоянными коэффициентами, является линейной стационарной системой. Примерами таких систем являются электрические схемы , собранные из резисторов , конденсаторов и катушек индуктивности (RLC-цепочки). Груз на пружинке также можно считать ЛСС.

Большая часть общих концепций ЛСС схожа как в случае непрерывных систем, так и в случае дискретных систем.

Стационарность и линейные преобразования

Рассмотрим нестационарную систему, чья импульсная характеристика представляет собой функцию двух переменных. Посмотрим, как свойство стационарности поможет нам избавиться от одного измерения. К примеру, пусть входной сигнал — ${\displaystyle x(t)}$ , где аргумент — числа действительной оси, то есть ${\displaystyle t\in \mathbb {R} }$ . Линейный оператор ${\displaystyle {\mathcal {H}}}$ показывает, как система отрабатывает этот входной сигнал. Соответствующий оператор для некоторого набора аргументов представляет собой функцию двух переменных:

${\displaystyle h(t_{1},t_{2}){\mbox{, }}t_{1},t_{2}\in \mathbb {R} .}$

Для дискретной системы:

${\displaystyle h[n_{1},n_{2}]{\mbox{, }}n_{1},n_{2}\in \mathbb {Z} .}$

Так как ${\displaystyle {\mathcal {H}}}$ — линейный оператор, воздействие системы на входной сигнал ${\displaystyle x(t)}$ представляется линейным преобразованием , описываемым следующим интегралом (интеграл суперпозиции)

${\displaystyle y(t_{1})=\int \limits _{-\infty }^{\infty }h(t_{1},t_{2})\,x(t_{2})\,dt_{2}.}$

Если линейный оператор ${\displaystyle {\mathcal {H}}}$ ко всему прочему является и стационарным, тогда

${\displaystyle h(t_{1},t_{2})=h(t_{1}+\tau ,t_{2}+\tau)\qquad \forall \,\tau \in \mathbb {R} .}$

Положив

${\displaystyle \tau =-t_{2},}$

получим:

${\displaystyle h(t_{1},t_{2})=h(t_{1}-t_{2},0).}$

Для краткости записи второй аргумент в ${\displaystyle h(t_{1},t_{2})}$ обычно опускается и интеграл суперпозиции становится интегралом свёртки:

${\displaystyle y(t_{1})=\int \limits _{-\infty }^{\infty }h(t_{1}-t_{2})\,x(t_{2})\,dt_{2}=(h*x)(t_{1}).}$

Таким образом, интеграл свёртки показывает как линейная отрабатывает любой входной сигнал. Полученное соотношение для дискретных систем:

${\displaystyle y[n_{1}]=\sum _{n_{2}=-\infty }^{\infty }h[n_{1}-n_{2}]\,x[n_{2}]=(h*x)[n_{1}].}$

Импульсная переходная функция

Если ко входу системы приложить входной сигнал в виде дельта-функции Дирака , результирующий выходной сигнал ЛСС будет представлять собой импульсную переходную функцию системы. Запись:

${\displaystyle (h*\delta)(t)=\int \limits _{-\infty }^{\infty }h(t-\tau)\,\delta (\tau)\,d\tau =h(t),}$

Для дискретной системы:

${\displaystyle x[n]=\sum _{m=-\infty }^{\infty }x[m]\delta [n-m].}$

(из-за свойства сдвига дельта-функции).

Заметим, что:

${\displaystyle h(t)=h(t,0)\ ({\mbox{with }}t=t_{1}-t_{2})}$

то есть ${\displaystyle h(t)}$ — импульсная переходная функция системы

Импульсная переходная функция используется для того, чтобы найти выходной сигнал системы как реакцию на любой входной сигнал. Кроме того, любой вход может быть представлен в виде суперпозиции дельта-функций:

${\displaystyle x(t)=\int \limits _{-\infty }^{\infty }x(\tau)\delta (t-\tau)\,d\tau }$

Приложив ко входу системы, получим:

${\displaystyle {\mathcal {H}}x(t)={\mathcal {H}}\int \limits _{-\infty }^{\infty }x(\tau)\delta (t-\tau)\,d\tau }$

${\displaystyle \quad =\int \limits _{-\infty }^{\infty }{\mathcal {H}}x(\tau)\delta (t-\tau)\,d\tau }$ (так как ${\displaystyle {\mathcal {H}}}$ линейна)

${\displaystyle \quad =\int \limits _{-\infty }^{\infty }x(\tau){\mathcal {H}}\delta (t-\tau)\,d\tau }$ (так как ${\displaystyle x(\tau)}$ постоянна по t и ${\displaystyle {\mathcal {H}}}$ линейна)

${\displaystyle \quad =\int \limits _{-\infty }^{\infty }x(\tau)h(t-\tau)\,d\tau }$ (by definition of ${\displaystyle h(t)}$ )

В импульсной переходной функции ${\displaystyle h(t)}$ содержится вся информация о динамике ЛСС.

Собственные функции

Собственная функция — функция, для которой выход оператора представляет собой ту же функцию, в общем случае с точностью до постоянного множителя. Запись:

${\displaystyle {\mathcal {H}}f=\lambda f}$ ,

где f — собственная функция, и ${\displaystyle \lambda }$ — собственное число , константа.

Экспоненты ${\displaystyle e^{st}}$ , где ${\displaystyle s\in \mathbb {C} }$ являются собственными функциями линейного стационарного оператора. Простое доказательство:

Пусть входной сигнал системы ${\displaystyle x(t)=e^{st}}$ . Тогда выходной сигнал системы ${\displaystyle h(t)}$ равен:

${\displaystyle \int \limits _{-\infty }^{\infty }h(t-\tau)e^{s\tau }d\tau }$

что эквивалентно следующему выражению в силу коммутативности свёртки:

${\displaystyle \int \limits _{-\infty }^{\infty }h(\tau)\,e^{s(t-\tau)}\,d\tau }$

${\displaystyle \quad =e^{st}\int \limits _{-\infty }^{\infty }h(\tau)\,e^{-s\tau }\,d\tau }$

${\displaystyle \quad =e^{st}H(s)}$ ,

где

${\displaystyle H(s)=\int \limits _{-\infty }^{\infty }h(t)e^{-st}dt}$

зависит только от s .

Таким образом, ${\displaystyle e^{st}}$ — собственная функция ЛСС.

Преобразования Лапласа и Фурье

Преобразование Лапласа

${\displaystyle H(s)={\mathcal {L}}\{h(t)\}=\int \limits _{-\infty }^{\infty }h(t)e^{-st}dt}$

является точным способом получить собственные числа из импульсной переходной функции. Особенный интерес представляют чистые синусоиды, то есть экспоненты вида ${\displaystyle \exp({j\omega t})}$ где ${\displaystyle \omega \in \mathbb {R} }$ и ${\displaystyle j}$ — мнимая единица . Они обычно называются комплексными экспонентами даже если аргумент не имеет действительной части. Преобразование Фурье ${\displaystyle H(j\omega)={\mathcal {F}}\{h(t)\}}$ даёт собственные числа для чисто комплексных синусоид. ${\displaystyle H(s)}$ называется передаточной функцией системы , иногда в литературе этот термин применяют и к ${\displaystyle H(j\omega)}$ .

Преобразование Лапласа обычно используется для односторонних сигналов, то есть при нулевых начальных условиях. Начальный момент времени без потери общности принимается за ноль, а преобразование берётся от ноля до бесконечности (преобразование, которое получается при интегрировании также и до минус бесконечности, называется двустороннее преобразование Лапласа ).

Преобразование Фурье используется для анализа систем, через которые проходят периодические сигналы, и во многих других случаях — например, для анализа системы на устойчивость .

Из-за свойств свёртки для обоих преобразований имеют место следующие соотношения:

${\displaystyle y(t)=(h*x)(t)=\int \limits _{-\infty }^{\infty }h(t-\tau)x(\tau)d\tau }$

${\displaystyle \quad ={\mathcal {L}}^{-1}\{H(s)X(s)\}}$

Для дискретных систем:

${\displaystyle y[n]=(h*x)[n]=\sum _{m=-\infty }^{\infty }h[n-m]x[m]}$

${\displaystyle \quad ={\mathcal {Z}}^{-1}\{H(s)X(s)\}}$

Некоторые свойства

Некоторые из важных свойств любой системы — причинность и устойчивость. Для того, чтобы система существовала в реальном мире, должен выполняться принцип причинности. Неустойчивые системы могут быть построены и иногда быть даже полезными.

Причинность

Система называется причинной, если её выход зависит только от текущего или предыдущего приложенного воздействия. Необходимое и достаточное условие причинности:

${\displaystyle h(t)=0\quad \forall t<0,}$

Для дискретных систем:

${\displaystyle h[n]=0\ \forall n<0,}$

где ${\displaystyle h(t)}$ — импульсная переходная функция. В явном виде определить причинная система или нет из её преобразования Лапласа в общем случае невозможно, так как обратное преобразование Лапласа не является уникальным. Причинность может быть определена когда задана .

Устойчивость

Система является устойчивой по ограниченному входу, ограниченному выходу ( англ. bounded input, bounded output stable, BIBO stable) если для каждого ограниченного входа выходной сигнал является конечным. Запись: Если

${\displaystyle ||x(t)||_{\infty }=\lim _{p\to \infty }\left(\int \limits _{-\infty }^{\infty }|x(t)|^{p}dt\right)^{1/p}<\infty }$

и

${\displaystyle ||y(t)||_{\infty }=\lim _{p\to \infty }\left(\int \limits _{-\infty }^{\infty }|y(t)|^{p}dt\right)^{1/p}<\infty }$

(то есть, максимумы абсолютных значений ${\displaystyle x(t)}$ и ${\displaystyle y(t)}$ конечны), тогда система устойчива. Необходимое и достаточное условие устойчивости: импульсная переходная характеристика системы, ${\displaystyle h(t)}$ , должна удовлетворять выражению

${\displaystyle ||h(t)||_{1}=\int \limits _{-\infty }^{\infty }|h(t)|dt<\infty .}$

Для дискретных систем:

${\displaystyle ||h[n]||_{1}=\sum _{n=-\infty }^{\infty }|h[n]|<\infty .}$

В частотной области область сходимости должна содержать мнимую ось ${\displaystyle s=j\omega }$ .

См. также

• АФЧХ
• ЛАФЧХ
• Системный анализ
• Передаточная функция
• Функция Грина
• Нелинейное управление

Ссылки

• P. P. Vaidyanathan and T. Chen. Role of anticausal inverses in multirate filter banks -- Part I: system theoretic fundamentals (англ.) // IEEE Trans. Signal Proc. : journal. — 1995. — May.
• P. P. Vaidyanathan and T. Chen. Role of anticausal inverses in multirate filter banks -- Part II: the FIR case, factorizations, and biorthogonal lapped transforms (англ.) // IEEE Trans. Signal Proc. : journal. — 1995. — May.
• В.И. Зубов. Теория уравнений управляемого движения (неопр.) . — Л. : ЛГУ, 1980.