Фа́за колеба́ний полная или мгновенная — аргумент периодической функции, описывающей колебательный или волновой процесс.

Фаза колебаний начальная — значение фазы колебаний (полной) в начальный момент времени, то есть при ${\displaystyle t=0}$ (для колебательного процесса), а также в начальный момент времени в начале системы координат, то есть при ${\displaystyle t=0}$ в точке с координатами ${\displaystyle (x,\ y,\ z)=0}$ (для волнового процесса).

Фаза колебания (в электротехнике ) — аргумент синусоидальной функции (напряжения, тока), отсчитываемый от точки перехода минусового значения через нуль к положительному значению и обратно .

Определения

Фаза колебания — гармоническое колебание ${\displaystyle \varphi .}$

Величину ${\displaystyle \varphi ,}$ входящую в аргумент функций косинуса или синуса , называют фазой колебаний описываемой этой функцией:

${\displaystyle \varphi =\omega t.}$

Как правило, о фазе говорят применительно к гармоническим колебаниям или монохроматическим волнам . При описании величины, испытывающей гармонические колебания, используется, например, одно из выражений:

${\displaystyle A\cos(\omega t+\varphi _{0}),}$

${\displaystyle A\sin(\omega t+\varphi _{0}),}$

${\displaystyle Ae^{i(\omega t+\varphi _{0})}.}$

Аналогично, при описании волны, распространяющейся в одномерном пространстве, например, используются выражения вида:

${\displaystyle A\cos(kx-\omega t+\varphi _{0}),}$

${\displaystyle A\sin(kx-\omega t+\varphi _{0}),}$

${\displaystyle Ae^{i(kx-\omega t+\varphi _{0})},}$

для волны в пространстве любой размерности (например, в трехмерном пространстве):

${\displaystyle A\cos({\vec {k}}\cdot {\vec {r}}-\omega t+\varphi _{0}),}$

${\displaystyle A\sin({\vec {k}}\cdot {\vec {r}}-\omega t+\varphi _{0}),}$

${\displaystyle Ae^{i({\vec {k}}\cdot {\vec {r}}-\omega t+\varphi _{0})}.}$

Фаза колебаний (полная) в этих выражениях — аргумент функции, то есть выражение, записанное в скобках; фаза колебаний начальная — величина ${\displaystyle \varphi _{0},}$ являющаяся одним из слагаемых полной фазы. Говоря о полной фазе, слово полная часто опускают.

Колебания с одинаковыми амплитудами и частотами могут различаться фазами. Так как:

${\displaystyle \omega =2\pi /T,}$ то ${\displaystyle \varphi =\omega t=2\pi t/T.}$

Отношение ${\displaystyle t/T}$ указывает, сколько периодов прошло от момента начала колебаний. Любому значению времени ${\displaystyle t,}$ выраженному в числе периодов ${\displaystyle T,}$ соответствует значение фазы ${\displaystyle \varphi ,}$ выраженное в радианах. Так, по прошествии времени ${\displaystyle t=T/4}$ (четверти периода) фаза будет ${\displaystyle \varphi =\pi /2,}$ по прошествии половины периода — ${\displaystyle \varphi =\pi ,}$ по прошествии целого периода ${\displaystyle \varphi =2\pi }$ и т. д.

Поскольку функции синус и косинус совпадают друг с другом при сдвиге аргумента (то есть фазы) на ${\displaystyle \pi /2,}$ то во избежание путаницы лучше пользоваться для определения фазы только одной из этих двух функций, а не той и другой одновременно. По обычному соглашению фазой считают аргумент косинуса , а не синуса .

То есть, для колебательного процесса (см. выше) фаза (полная):

${\displaystyle \varphi =\omega t+\varphi _{0},}$

для волны в одномерном пространстве:

${\displaystyle \varphi =kx-\omega t+\varphi _{0},}$

для волны в трехмерном пространстве или пространстве любой другой размерности:

${\displaystyle \varphi ={\vec {k}}\cdot {\vec {r}}-\omega t+\varphi _{0}}$ ,

где ${\displaystyle \omega }$ — угловая частота (величина, показывающая, на сколько радиан или градусов изменится фаза за 1 с; чем величина выше, тем быстрее растет фаза с течением времени);

${\displaystyle t}$ — время ;

${\displaystyle \varphi _{0}}$ — начальная фаза (то есть фаза при ${\displaystyle t=0);}$

${\displaystyle k}$ — волновое число ;

${\displaystyle x}$ — координата точки наблюдения волнового процесса в одномерном пространстве;

${\displaystyle {\vec {k}}}$ — волновой вектор ;

${\displaystyle {\vec {r}}}$ — радиус-вектор точки в пространстве (набор координат, например, декартовых ).

В приведенных выше выражениях фаза имеет размерность угловых единиц ( радианы , градусы ). Фазу колебательного процесса по аналогии с механическим вращательным также выражают в циклах , то есть долях периода повторяющегося процесса:

1 цикл = ${\displaystyle 2\pi }$ радиан = 360 угловых градусов.

В аналитических выражениях (в формулах) преимущественно (и по умолчанию) используется представление фазы в радианах, представление в градусах также встречается достаточно часто (по-видимому, как предельно явное и не приводящее к путанице, поскольку знак градуса не принято никогда опускать ни в устной речи, ни в записях). Указание фазы в циклах или периодах (за исключением словесных формулировок) в технике сравнительно редко.

Иногда (в квазиклассическом приближении , где используются квазимонохроматические волны, то есть близкие к монохроматическим, но не строго монохроматические, а также в формализме интеграла по траекториям , где волны могут быть и далекими от монохроматических, хотя всё же подобны монохроматическим) рассматривается фаза, являющаяся нелинейной функцией времени ${\displaystyle t}$ и пространственных координат ${\displaystyle {\vec {r}},}$ в принципе — произвольная функция :

${\displaystyle \varphi =\varphi ({\vec {r}},t).}$

Связанные термины

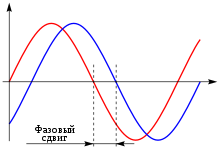
Рассматривая два колебательных процесса одинаковой частоты, говорят о постоянной разности полных фаз (о сдвиге фаз ) этих процессов. В общем случае сдвиг фаз может меняться во времени, например, из-за угловой модуляции одного или обоих процессов.

Если два колебательных процесса происходят одновременно (например, колеблющиеся величины достигают максимума в один и тот же момент времени), то говорят, что они находятся в фазе (колебания синфазны ). Если моменты максимума одного колебания совпадают с моментами минимума другого колебания, то говорят, что колебания находятся в противофазе (колебания противофазны ). Если разность фаз составляет ±90°, то говорят, что колебания находятся в квадратуре или что одно из этих колебаний — квадратурное по отношению к другому колебанию (опорному, «синфазному», то есть служащему для условного определения начальной фазы).

Если амплитуды двух противофазных монохроматических колебательных процессов одинаковы, то при сложении таких колебаний (при их интерференции ) в линейной среде происходит взаимное уничтожение колебательных процессов.

Действие

Действие - одна из наиболее фундаментальных физических величин, на которой построено современное описание практически любой достаточно фундаментальной физической системы — по своему физическому смыслу является фазой волновой функции .

Примечания

Литература

• Стрелков С. П. Введение в теорию колебаний. Учебник для вузов. 4-е изд., стер.. — М. : Лань-Пресс, 2021. — 440 с.