Дифракция Фраунгофера
- 1 year ago
- 0
- 0

Дифра́кция во́лн (в старой литературе также диффракция , от лат. diffractus ; букв. — «разломанный») — явление огибания волнами препятствий , в широком смысле любое отклонение от законов геометрической оптики при распространении волн . Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы .
Изначально явление дифракции трактовалось как огибание волной препятствия, то есть проникновение волны в область геометрической тени. Со временем с дифракцией стали связывать весьма широкий круг явлений, возникающих при распространении волн в случае учёта их пространственного ограничения . Во многих случаях дифракция может быть и не связана с огибанием препятствия (но всегда обусловлена его наличием). Такова, например, дифракция на прозрачных, так называемых фазовых, структурах.
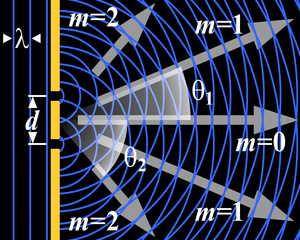
Общим свойством всех явлений дифракции является зависимость степени её проявления от соотношения между длиной волны λ и размером ширины волнового фронта D , который может быть ограничен непрозрачным экраном на пути его распространения, а может быть следствием неоднородностей структуры самой волны: исходное строение волнового поля подвержено существенной трансформации в случае, если его элементы сравнимы с длиной волны или меньше её.
Ограничение ширины волнового фронта существует всегда, и явление дифракции сопровождает любой процесс распространения волн, поэтому наиболее тонкие вопросы практической оптики, которая во всех остальных случаях рассчитывается в приближении геометрической оптики, решаются при помощи теории дифракции. Так, например, дифракция задаёт предел разрешающей способности любого оптического прибора, который невозможно преступить принципиально при конечной длине волны излучения, которое используется для создания изображений .
Дифракция волн может проявляться:
Наиболее хорошо изучена дифракция электромагнитных (в частности, оптических ) и звуковых волн, а также волн (волны на поверхности жидкости).
Общим условием применимости законов геометрической оптики можно считать тот случай, когда длина волны бесконечно мала по сравнению с размерами волнового фронта. Это предельный, идеализированный, не встречающийся в природе случай .
Ограниченный в пространстве волновой пучок имеет свойство «расходиться» («расплываться») в пространстве по мере распространения даже в однородной среде. Данное явление не описывается законами геометрической оптики и относится к дифракционным явлениям (дифракционная расходимость, дифракционное расплывание волнового пучка). Нерасходящийся параллельный пучок, то есть луч, то есть ограниченную в пространстве область прямолинейного волнового фронта , принципиально невозможно создать. Величина разброса пучка шириной D (по половине интенсивности) имеет порядок . Например, если точечный источник света создаёт резкую тень, геометрически подобную препятствию, на экране, расположенном на небольшом расстоянии R, то линейный размер дифракционных полос, который имеет значение порядка , может оказаться заметным даже для относительно мало расходящихся пучков при большом R .
Таким образом, дифракция сказывается на резкости фотографий: хотя закрытие диафрагмы (уменьшение относительного отверстия ) приводит к увеличению глубины резкости , образование оптической системой диска Эйри может сводить этот эффект на нет. Для каждой фотокамеры существует свой предел регулирования диафрагмы, при котором отрицательные эффекты дифракции ещё не возникают [ неавторитетный источник ] .
При распространении излучения в оптически неоднородных средах дифракционные эффекты заметно проявляются при размерах неоднородностей, сравнимых с длиной волны. При размерах неоднородностей, превышающих длину волны на 3—4 порядка и более, явлением дифракции, как правило, можно пренебречь. С другой стороны, если размер неоднородностей среды сравним с длиной волны, в таком случае дифракция проявляет себя в виде явления [ источник не указан 256 дней ] .
Дифракция неразрывно связана с явлением интерференции . Фейнман вообще не различает эти явления, считая различие в терминологии делом привычки: при малом количестве источников говорят об интерференции, а при большом — о дифракции . Со времён Френеля явление дифракции трактуют как случай интерференции вторичных волн .
В средах, в которых скорость волны плавно (по сравнению с длиной волны) меняется от точки к точке, распространение волнового пучка является криволинейным (см. градиентная оптика , градиентные волноводы, мираж ). При этом волна также может огибать препятствие, однако такое криволинейное распространение волны может быть описано с помощью уравнений геометрической оптики.
Вращение плоскости поляризации световой волны в оптически активной среде дифракцией не является, хотя и единственным результатом так называемой коллинеарной дифракции с преобразованием оптических может быть именно поворот плоскости поляризации , в то время как дифрагированный волновой пучок сохраняет исходное направление распространения. Такой тип дифракции может быть реализован, например, как дифракция света на ультразвуке в двулучепреломляющих кристаллах, при которой волновые векторы оптической и акустической волн параллельны друг другу.
С точки зрения геометрической оптики невозможно объяснить явления, имеющие место в так называемых связанных волноводах, хотя эти явления также не относят к дифракции (волновые явления, связанные с «вытекающими» полями).
Оптика кристаллов, имеющая дело с оптической анизотропией среды, также имеет лишь косвенное отношение к проблеме дифракции, хотя и нуждается в корректировке используемых представлений геометрической оптики, что связано с различием в понятии луча (как направления распространения света) и направления распространения волнового фронта (то есть направления нормали к нему)
Отступление от прямолинейности распространения света наблюдается также в сильных полях тяготения. Экспериментально подтверждено, что свет, проходящий вблизи массивного объекта, например, вблизи звезды, отклоняется в её поле тяготения в сторону звезды. Таким образом, и в данном случае можно говорить об «огибании» световой волной препятствия, однако, это явление также не относится к дифракции.
Первая волновая теория дифракции с привлечением интерференции к объяснению дифракционных картин дана Томасом Юнгом . Юнг предположил, что существует передача амплитуды колебаний, поперечная к направлению распространения волны, то есть не только перпендикулярно волновому фронту, но и вдоль него. Скорость этой передачи (поток амплитуды) пропорционален длине волны и различию ( градиенту ) амплитуд на фронте. По Юнгу дифрагированная волна возникает локально в некоторой окрестности границы геометрической тени за краем препятствия. Совершенно симметрично дифрагированная волна образуется и в «освещённой» области пространства, то есть край препятствия является источником цилиндрических волн. Интерференция прошедших и дифрагированных волн создаёт создаёт полосы на краю тени .
Слабым местом теории Юнга, которое показал Френель , оказалась неспособность объяснить тот факт, что острый и закруглённый края препятствия создают совершенно одинаковые дифракционные картины. Френель отказался от локальной трактовки дифрагировавших волн и воспользовался принципом Гюйгенса , с помощью которого описал дифракционные картины как результат интерференции бесконечного множества фиктивных точечных вторичных источников, распространённых по всей плоскости отверстия .
В строгой формулировке Гельмгольца и Кирхгофа математическая задача дифракции волн с помощью принципа Гюйгенса формулируется в виде интегрального уравнения, решить которое в общем случае, как правило, не удаётся. Рассчитать дифракционное поле на основе принципа Гюйгенса получается, как правило, только если указаны краевые условия .
Приближённое решение задачи получается при отверстии, большом по сравнению с длиной волны, по Кирхгофу пользуются следующими упрощениями :
Таким образом может быть получено приближённое решение дифракционного поля как для конечных расстояний от отверстия (случай расходящихся пучков, то есть сферических волн — дифракция Френеля ), так и для удалённой зоны (случай приближённо параллельных пучков, то есть плоских волн — дифракция Фраунгофера ) .

Рассмотрим монохроматическую плоскую волну с амплитудой с длиной волны , падающую на экран с щелью ширины .
Будем считать, что щель находится в плоскости x′ − y′ с центром в начале координат. Тогда может предполагаться, что дифракция производит волну ψ , которая расходится радиально. Вдали от разреза можно записать
Пусть ( x′ , y′ , 0) — точка внутри разреза, по которому мы интегрируем. Мы хотим узнать интенсивность в точке ( x , 0, z). Щель имеет конечный размер в x направлении (от до ) и бесконечна в y направлении ([ ]).
Расстояние r от щели определяется как:
Предполагая случай дифракции Фраунгофера , получим условие Другими словами, расстояние до точки наблюдения много больше характерного размера щели (ширины).
Используя биномиальное разложение и пренебрегая слагаемыми второго и выше порядков малости, можно записать расстояние в виде:
Видно, что 1/ r перед уравнением не осциллирует, то есть даёт малый вклад в интенсивность по сравнению с экспоненциальным множителем. Тогда его можно записать приближённо как z .
Здесь мы введём некую константу C , которой обозначим все постоянные множители в предыдущем уравнении. Она в общем случае может быть комплексной, но это не важно, так как в конце нас будет интересовать только интенсивность, и нам будет интересен только квадрат модуля.
В случае дифракции Фраунгофера мало, поэтому Такое же приближение верно и для Таким образом, считая приходим к выражению:
Используя формулу Эйлера и её производную: и
где ненормированная функция sinc(x) определена как
Подставляя в последнее выражение для амплитуды, можно получить ответ для интенсивности в виде волны в зависимости от угла θ :
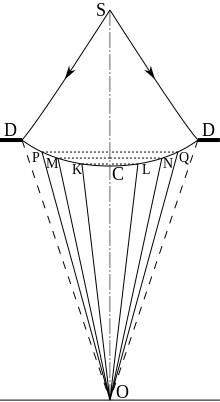
Дифракция Френеля наблюдается в расходящихся пучках (точечный источник) на круглом отверстии в непрозрачном экране или на круглом непрозрачном препятствии . Теория Френеля даёт правильное значение амплитуды результирующей волны (т. е. освещённости дифракционной картины в данной точке), пока размеры отверстий и препятствий велики по сравнению с длиной волны, т. е. углы дифракции малы .
Рассмотрим случай дифракции света от точечного источника S, который проходит сквозь круглое отверстие DD и падает на экран, где наблюдается дифракционная картина в точке О, в которой ось симметрии системы пересекает экран. Сферический волновой фронт разрежем коническими поверхностями OKL, OMN, OPQ и т. д. так, чтобы длины образующих этих конусов OK, OM, OP отличались друг от друга на половину длины волны. Таким образом волновой фронт разрезается на зоны Френеля. Свет, приходящий в точку O из любых двух соседних зон при интерференции даёт минимум. Поскольку количество света пропорционально площади зоны, а зоны эти имеют приблизительно одинаковую площадь (так как разность хода в половину длины волна мала по сравнению с размерами отверстия и расстояниями в оптической системе), этот минимум соответствует почти полному гашению света . Таким образом, в монохроматическом свете :
В белом свете, поскольку деление на зоны зависит от длины волны , кольца получаются цветными .
Для определения картины дифракции в точке, находящейся в стороне от оси симметрии оптической системы, дифракционную картину поворачивают относительно источника света, пока ось симметрии не пройдёт через интересующую точку. При этом зоны Френеля поворачиваются относительно отверстия или препятствия, и новое число открытых (или закрытых) зон даёт в выбранной точке минимум или максимум .
Радиус m-й зоны Френеля можно вычислить по следующему соотношению :
Прозрачный экран, в котором все чётные или все нечётные зоны зачернены (может быть изготовлен, например, фотографированием чертежа или колец Ньютона на пластинку или плёнку с большим уменьшением) называется зональной пластинкой .
Расположив источник и экран на тех расстояниях, на которые зональная пластинка рассчитана, с помощью пластинки, на которой открыты все чётные (0-я, 2-я, 4-я и т. д.) зоны, можно получить интуитивно неочевидный, но теоретически предсказуемый результат: так как пластинка исключает гасящую интерференцию, с её помощью можно получить в точке в центре экрана освещённость почти вдвое больше, чем без пластинки. Такая зонная пластинка действует как собирательная линза .
Зонная пластинка, в которой свет чётных зон не поглощается, а лишь получает дополнительную разность хода в половину длины волны, создаёт ещё вдвое больше света по сравнению с поглощающей пластинкой (вчетверо больше, чем от такого же размера отверстия). Роберт Вуд изготовил такую пластинку, снимая слой лака, нанесённый на стекло, пока оптическая разность хода не достигла половины длины волны .
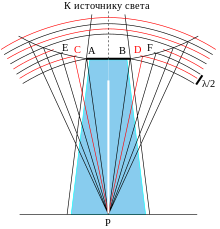

Картина дифракции на непрозрачном диске описывается тем же методом, который приводит, однако, к иным результатам. Непрозрачный диск закрывает зоны Френеля от m-й до бесконечности, и уже неважно, чётно ли m или нечётно . В центре тени от диска всегда остаётся светлое пятно Пуассона .
Таким образом, наиболее заметные различия дифракционных картин от отверстия и от диска следующие :
Академик Пуассон в 1818 году выдвинул предсказанное из теории Френеля светлое пятно в центре тени в качестве наиболее яркого парадокса, который доказывает несостоятельность этой теории. При расстояниях порядка 10 км диаметр центральной зоны Френеля составляет для красного света (650 нм) — 12 см, что приблизительно соответствует размеру небольшой тарелки. Опыт с такими параметрами установки был произведён Араго , и светлое пятно Пуассона в центре тени наблюдалось в полном согласии с теорией Френеля .
Светлое пятно в центре тени от шариков различного размера столетием раньше (1715) наблюдал французский астроном Делиль , но этот не получивший объяснения опыт был совершенно забыт .
Исследованием дифракции радиоволн занимается
Дифракцию рентгеновских лучей можно наблюдать, направив их на кристалл , она используется в рентгеноструктурном анализе для определения структуры кристалла. Кроме того, дифракцию рентгеновских лучей можно получить, направив их на обычную дифракционную решётку (то есть, используемую для наблюдения дифракции видимого излучения ) так, чтобы угол падения был достаточно близок к 90 градусам , этим способом можно измерить длину волны рентгеновских лучей .
Одним из наглядных примеров дифракции света на ультразвуке является дифракция света на ультразвуке в жидкости. В одной из постановок такого эксперимента в оптически-прозрачной ванночке в форме прямоугольного параллелепипеда с оптически-прозрачной жидкостью с помощью пластинки из пьезоматериала на частоте ультразвука возбуждается стоячая волна . В её узлах и пучностях оптическая плотность среды различается. Таким образом ванночка с водой становится для световой волны фазовой дифракционной решёткой, на которой осуществляется дифракция в виде изменения фазовой структуры волн, что можно наблюдать в оптический микроскоп методом фазового контраста или методом тёмного поля .

Дифракция от трехмерной периодической структуры, такой как атомы в кристалле называется дифракцией Брегга. Это похоже на то, что происходит, когда волны рассеиваются на дифракционной решётке. Брегговская дифракция является следствием интерференции между волнами, отражёнными от кристаллических плоскостей. Условие возникновения интерференции определяется законом Вульфа-Брегга:
где
Брегговская дифракция может осуществляться при использовании света с очень маленькой длиной волны, такого как рентгеновское излучение , либо волны материи, такие как нейтроны и электроны , длины волн которых сравнимы или много меньше, чем межатомное расстояние . Получаемые данные дают информацию о межплоскостных расстояниях, что позволяет вывести кристаллическую структуру. Дифракционный контраст, в электронных микроскопах и , в частности, также является мощным инструментом для изучения отдельных дефектов и локальных полей деформации в кристаллах.
Дифракция частиц — это упругое рассеяние микрочастиц ( электронов , нейтронов, атомов и т. п.) на кристаллах или молекулах жидкостей или газов. При этом из начального пучка частиц возникают дополнительные отклонённые пучки, причём направление отклонения и интенсивность пучков зависят от строения объекта. Решение уравнения Шрёдингера для свободной частицы имеет вид плоской волны. Проходя через объект, волна встречает некоторое распределение потенциальной энергии, связанное со строением объекта и характером его взаимодействия с частицей, в результате чего начальная волна испытывает рассеяние. Дифракционная картина описывается решением волнового уравнения, а квадрат модуля пси-функции определяет вероятность обнаружения частицы в данной точке пространства .
Задача о дифракции частиц распадается на две подзадачи: рассеяние частиц одиночными атомами и получение интерференционной картины с учётом взаимного расположения атомов. В рассеянии на одиночных атомах проявляется специфика взаимодействия с ними тех или иных видов частиц. Законы интерференции волн, исходящих из данных рассеивающих центров, напротив, для всех частиц и электромагнитных волн общие, поэтому многие явления дифракции частиц аналогичны дифракции света . Например, когда нейтроны рассеиваются тяжёлым ядром, и длина волны нейтронов мала по сравнению с радиусом ядра, движение нейтронов происходит квазиклассическим образом, и рассеяние их есть результат слабого отклонения, аналогичного фраунгоферовской дифракции света на шарике .
Процесс дифракции электронов и нейтронов получил широкое применение в аналитических исследованиях кристаллических структур металлов, сплавов, полупроводниковых материалов .
Основы теории дифракции были заложены при изучении дифракции света в первой половине XIX века в трудах Юнга (1800) и Френеля (1815) . Значительный вклад в изучение дифракции внесли Гримальди , Гюйгенс , Араго , Пуассон , Гаусс , Фраунгофер , Бабине , Кирхгоф , Аббе , У. Г. Брэгг и У. Л. Брэгг , фон Лауэ , Роуланд , Зоммерфельд , Леонтович , Фок , , Цернике .
Обнаружение дифракции электронов в 1927 году (опыт Дэвиссона и Джермера) сыграло большую роль в подтверждении существования волн де Бройля и в подтверждении концепции корпускулярно-волнового дуализма (идеи двойственной природы волн и частиц). В XX и XXI веках продолжились исследования дифракции волн на сложных структурах.
Дифракционные методы — это совокупность методов исследования атомного строения вещества, использующих дифракцию пучка фотонов , электронов или нейтронов , рассеиваемого исследуемым объектом.
В дифракционных методах измеряют зависимость интенсивности рассеянного излучения от направления, то есть функцию I (φ,θ). При этом длина волны после рассеяния не изменяется. Имеет место так называемое упругое рассеяние . В основе дифракционных методов лежит простое соотношение для длины волны и расстояния между рассеивающими атомами.