CubeHash — это параметризуемое семейство криптографических хеш-функций CubeHash r/b . CubeHash8/1 была предложена в качестве нового стандарта для SHA-3 в конкурсе хеш-функций, проводимым Национальным институтом стандартов и технологий (НИСТ) . Вначале НИСТ требовал около 200 циклов на байт . После некоторых уточнений от НИСТ автор сменил параметры на CubeHash16/32, которая примерно в 16 раз быстрее, чем CubeHash8/1 и легко догоняет SHA-256 и SHA-512 на различных платформах .

CubeHash прошла во второй раунд конкурса, но так и не попала в пятёрку финалистов .

Описание алгоритма

Работа CubeHash r/b-h базируется на трёх параметрах: r , b и h .

• r — количество раундов (не менее 1)
• b — размер блока в байтах (от 1 до 128)
• h — размер хеша в битах (может быть 8, 16, 24, 32, …, 512)

Алгоритм имеет 5 основных шагов:

• инициализация 128-байтового состояния как функция ( h , b , r )
• разбиение входящего сообщения на части. Каждая часть включает один или более b -байтовых блоков
• для каждого b -байтового блока части сообщения: выполняется операция исключающего «ИЛИ» над блоком и первыми b байтами состояния и затем преобразует его посредством r одинаковых раундов
• завершение состояния
• вывод первых h /8 байт состояния

Инициализация. 128-байтовое состояние рассматривается как последовательность 32 четырёх-байтовых слов x ₀₀₀₀₀ , x ₀₀₀₀₁ , x ₀₀₀₁₀ ,…, x ₁₁₁₁₁ , каждое из которых представляется в little-endian форме 32-битовых целых чисел. Первые три слова x ₀₀₀₀₀ , x ₀₀₀₀₁ , x ₀₀₀₁₀ выставляются в h /8, b , r соответственно. Оставшиеся слова равны нулю. Затем состояние преобразуется посредством 10 r одинаковых раундов.

Заполнение. Добавляется 1 бит ко входящему сообщению, затем оно дополняется минимально возможным количеством нулевых битов так, чтобы количество битов было кратно 8 b .

Заполнение не требует разделение хранилища длины сообщения, блока для обработки и остального. Реализация может хранить одиночное число между 0 и 8 b , чтобы записать число бит обработанных на данный момент в текущем блоке.

Завершение. К последнему состоянию слова x ₁₁₁₁₁ по модулю два прибавляется 1. Далее состояние преобразуется путём проведения 10 r одинаковых раундов.

Каждый раунд включает 10 шагов:

• прибавление x _{0 jklm} к x _{1 jklm} по модулю 2 ³² для каждого ( j, k, l, m )
• смещение влево по кругу на 7 бит слова x _{0 jklm} для каждого ( j, k, l, m )
• обмен x _{00 klm} c x _{01 klm} для каждого ( k, l, m )
• прибавление по модулю 2 числа x _{1 jklm} к x _{0 jklm} для каждого ( j, k, l, m )
• обмен x _{1 jk 0 m} с x _{1 jk 1 m} для каждого ( j, k, m )
• прибавление x _{0 jklm} к x _{1 jklm} по модулю 2 ³² для каждого ( j, k, l, m )
• смещение влево по кругу на 11 бит слова x _{0 jklm} для каждого ( j, k, l, m )
• обмен x _{0 j 0 lm} с x _{0 j 1 lm} для каждого ( j, l, m )
• прибавление по модулю 2 числа x _{1 jklm} к x _{0 jklm} для каждого ( j, k, l, m )
• обмен x _{1 jkl 0} с x _{1 jkl 1} для каждого ( j, k, l )

Особенности алгоритма

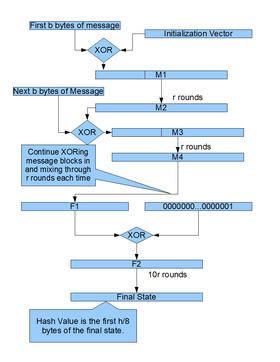
Алгоритм CubeHash не включает в себя блоки счётчиков, блоки, использующие случайные числа, и тому подобные блоки. Без этих блоков легче найти состояние, в котором происходит коллизия , но этот аргумент не работает, когда размер состояния довольно большой. Обычная атака на CubeHash должна сделать 2^400 попыток для нахождения коллизии 1024 битного состояния для CubeHash. Также нет необходимости нарушать любую симметрию, которая используется в раундах .

Инициализирующее состояние CubeHash не является симметричным, если параметр b не очень большой, то у злоумышленника не хватит вычислительной мощности, чтобы вычислить симметричное состояние или пару состояний.

Основные операции, используемые в CubeHash, это:

• прибавление 32 битного числа,
• выполнение операции исключающего ИЛИ над 32 битными числами и
• фиксированный сдвиг влево или вправо.

Эти операции выполняются за постоянное время на типичных процессорах. Большинство реализаций позволит избежать утечек с различных программных уровней. Например, для большинства реализаций программного обеспечения, использующих AES , возможна утечка через ключей через кэш . Этот факт заставил Intel добавить постоянную времени , связанную с AES.

Скорость работы

На конкурсе SHA -3 НИСТ проводил тестирование предложенных функций, одной из них была CubeHash с параметрами 16/32. Тестирование проводилось на двух процессорах Intel Core 2 Duo 6f6 (katana) и Intel Core 2 Duo E8400 1067a (brick):

• 11,47 циклов/байт: CubeHash16/32, brick, архитектура AMD64.

• 12,60 циклов/байт: SHA-512, brick, архитектура AMD64.

• 12,60 циклов/байт: SHA-512, katana, архитектура AMD64.

• 12,66 циклов/байт: CubeHash16/32, katana, архитектура AMD64.

• 12,74 циклов/байт: CubeHash16/32, brick, архитектура x86.

• 14,07 циклов/байт: CubeHash16/32, katana, архитектура x86.

• 15,43 циклов/байт: SHA-256, brick, архитектура x86.

• 15,53 циклов/байт: SHA-256, brick, архитектура amd64.

• 15,56 циклов/байт: SHA-256, katana, архитектура AMD64.

• 17,76 циклов/байт: SHA-512, brick, архитектура x86.

• 20,00 циклов/байт: SHA-512, katana, архитектура x86.

• 22,76 циклов/байт: SHA-256, katana, архитектура x86.

CubeHash не уступает в скорости своим оппонентам.

Примеры хешей

Данный пример использует CubeHash 8/1-512.

Инициализирующий вектор одинаковых для всех 8/1-512 хешей и выглядит как:

6998f35dfb0930c760948910e626160f36077cf3b58b0d0c57cf193d3341e7b8\ a334805b2089f9ef31ffc4142aef3850fe121839e940a4527d5293a27045ca12\ 9358096e81bf70349a90a44a93c33edb14c3e9844a87dbd0bc451df25212b3ac\ 6aabe51c5df0f63bddbb8ae8fad3cf0fd52582fbad2e2446094025a521a23d5c 

Хеширование ASCII сообщения «Hello» (hex: 0x48, 0x65, 0x6c, 0x6c, 0x6f) использует 6 блоков. Первые 5 блоков приходят (так как в данном случае каждая буква — один байт) из сообщения и ещё один блок для заполнения.

Значение 512-битового хеша равно:

7ce309a25e2e1603ca0fc369267b4d43f0b1b744ac45d6213ca08e7567566444\ 8e2f62fdbf7bbd637ce40fc293286d75b9d09e8dda31bd029113e02ecccfd39b 

Небольшое изменение в сообщении (например, изменение одного бита) ведёт к значительному изменению хеша (так называемый лавинный эффект ).

Для примера возьмём сообщение «hello», отличающееся от «Hello» всего в один бит. Хеш этого сообщения равен:

01ee7f4eb0e0ebfdb8bf77460f64993faf13afce01b55b0d3d2a63690d25010f\ 7127109455a7c143ef12254183e762b15575e0fcc49c79a0471a970ba8a66638 

Изменение параметров

CubeHash r/b-h принимает много различных параметров, используемых для определения хеша. Это придаёт гибкость алгоритму по отношению к конечному пользователю, который сам определяет наилучшие параметры для использования. Ниже представлены некоторые примеры хешей различных сообщений, использующие разные параметры алгоритма. Все сообщения записаны в ASCII. Три параметра, используемые в генерации хеша, представлены в r/b-h формате.

Сообщение: "" (пустая строка, строка с нулевой длинной) CubeHash 16/32-512: 4a1d00bbcfcb5a9562fb981e7f7db3350fe2658639d948b9d57452c22328bb32\ f468b072208450bad5ee178271408be0b16e5633ac8a1e3cf9864cfbfc8e043a CubeHash 8/1-512: 90bc3f2948f7374065a811f1e47a208a53b1a2f3be1c0072759ed49c9c6c7f28\ f26eb30d5b0658c563077d599da23f97df0c2c0ac6cce734ffe87b2e76ff7294 CubeHash 1/1-512: 3f917707df9acd9b94244681b3812880e267d204f1fdf795d398799b584fa8f1\ f4a0b2dbd52fd1c4b6c5e020dc7a96192397dd1bce9b6d16484049f85bb71f2f CubeHash 16/32-256: 44c6de3ac6c73c391bf0906cb7482600ec06b216c7c54a2a8688a6a42676577d CubeHash 8/1-256: 38d1e8a22d7baac6fd5262d83de89cacf784a02caa866335299987722aeabc59 CubeHash 1/1-256: 80f72e07d04ddadb44a78823e0af2ea9f72ef3bf366fd773aa1fa33fc030e5cb 

Сообщение: "Hello" CubeHash 16/32-512: dcc0503aae279a3c8c95fa1181d37c418783204e2e3048a081392fd61bace883\ a1f7c4c96b16b4060c42104f1ce45a622f1a9abaeb994beb107fed53a78f588c CubeHash 8/1-512: 7ce309a25e2e1603ca0fc369267b4d43f0b1b744ac45d6213ca08e7567566444\ 8e2f62fdbf7bbd637ce40fc293286d75b9d09e8dda31bd029113e02ecccfd39b CubeHash 1/1-512: 13cf99c1a71e40b135f5535bee02e151eb4897e4de410b9cb6d7179c677074eb\ 6ef1ae9a9e685ef2d2807509541f484d39559525179d53838eda95eb3f6a401d CubeHash 16/32-256: e712139e3b892f2f5fe52d0f30d78a0cb16b51b217da0e4acb103dd0856f2db0 CubeHash 8/1-256: 692638db57760867326f851bd2376533f37b640bd47a0ddc607a9456b692f70f CubeHash 1/1-256: f63041a946aa98bd47f3175e6009dcb2ccf597b2718617ba46d56f27ffe35d49 

Безопасность

Стойкость этого алгоритма увеличивается как при уменьшении b к 1, так и при увеличении r .
Поэтому CubeHash 8/1-512 стойче (более безопаснее) чем CubeHash 1/1-512, а CubeHash 1/1-512 стойче чем CubeHash 1/2-512. Самый слабый из возможных версий данного алгоритма — это CubeHash 1/128- h . Однако, безопасность зависит от времени. Более безопасный вариант будет дольше вычислять хеш-значение.

Возможные атаки

Атаки использующие структуру хеш-функции, как правило, самые успешные из всевозможных видов атак. Такие атаки могут найти коллизии, прообразы и вторые прообразы. Однако отличительная черта таких атак — это то, что они почти всегда разрабатываются для конкретной хеш-функции, потому что такие атаки используют конкретную реализацию вычисления состояний .

Атака на основе одного блока

Так как раунд вычислений в CubeHash является обратимым, то начальное состояние может быть вычислено путём произведения обратных операция над конечным состоянием. Атака на основе одного блока основана на этом обстоятельстве.

Рассмотрим алгоритм этой атаки.

Возьмём хеш H некоторого сообщения, b байт второго прообраза сообщения вычисляются, используя CubeHashr/b-h .

1. Установим первые h/8 байт финального состояния, используя хеш H , а оставшиеся 128-h/8 байт, используя пробное значение T , получаем состояние 6. Метод выбора пробного значения будет описан далее.
2. Применяя 10r обратных раундов к состоянию 6, получаем состояние 5. Обратные раунды функции можно получить, делая шаги алгоритма в обратном порядка, то есть, заменяя смещения по кругу влево на смещения по кругу вправо и сложение заменяя вычитанием по модулю 2 ³² .
3. Применим операцию исключающего или к 1 и последнему слову состояния 5, таким образом, получаем состояние 4
4. Сделав r обратных раундов с состоянием 4, получаем состояние 3.
5. Применим операцию исключающего или к сообщения 0x80 и первым байтом состояния 4, получив в итоге состояние 3.
6. Сделав r обратных раундов с состоянием 2, получаем состояние 1.
7. Если последние 128 — b байт состояния 1 не совпадают с 128-b байт инициализирующего вектора (состояние 0), тогда пробное сообщение было неудачно выбрано.
8. В противном случае пробное сообщение выбрано удачно. Второй прообраз вычисляется, используя исключающее или над первыми b байтами состояния 1 и первыми b байтами состояния инициализирующего вектора.

Повторяя описанную выше процедуру с различными значениями T , в конечном итоге будет сгенерирован второй прообраз. Метод выбора значения T не является критичным. Например, последовательность чисел следующих друг за другом может быть использована.

Предполагая, что CubeHash (в прямом или обратном сообщении) ведёт себя, как случайное отображение для произвольного пробного значения T, тогда вероятность того, что последние 128-b байт состояния 1 будут равны соответствующим байтам инициализирующего вектора равна 2 ^−8(128-b) . Таким образом, число пробных сообщений перед достижением успеха 2 ^8(128-b) . Если 2 ^8(128-b) < 2 ^h тогда атака на основе одного блока найдет второй прообраз за меньшее количество попыток, по сравнению с полным перебором. Другими словами атака на основе одного блока более эффективна, чем полный перебор для следующих значения h = 224 и b > 100 , для h = 256 и b > 96 , для h=384 и b> 80 , для h=512 и b > 64 .

Однако ожидаемое число попыток нужных для достижения успеха не зависит от числа раундов r. Время нужное для осуществления атаки увеличивается линейно от r, а не как показательная функция. Для b = 128 любое значение T будет сразу являться вторым прообразом.

Рассмотрим алгоритм улучшения атаки нахождения первого прообраза.

1. Исходя из значений ( h , b , r ) вычисляем инициализирующий вектор (состояние 0).
2. Для h бит и 1024-h , выполняем 10r обратных раундов и операцию исключающего или, чтобы получить состояние f .
3. Находим две n блочные последовательности, которые отображают состояние 0 и состояние f , в два состояния, которые имеют одинаковые последние 1024-h бит.

Существует 2 ^nb возможных входных n блоков и одного из них произойдет коллизия. Число попыток нужных для нахождения коллизии оценивается как

2 * (521 / b — 4) * 2 ^{512 — 4b} = 2 * 522 — 4b — logb

Кроме того учтём, что каждый раунд требует 2 ¹¹ битовых операция, тогда формула изменится на 2 ^{533-4b-logb+logr} битовых операций. Ускорение данной атаки может быть достигнуто за счёт того, что поиск коллизии будем производить не только после вычисления n-го блока, но и в каждом различном состоянии которого мы достигли (будем использовать и промежуточные состояния). Таким образом мы избавимся от множителя (512/b-4) . Тогда число попыток нужных для нахождения коллизии будет оцениваться как 2 ^513-4b битовых операций. Рассмотрим CubeHash-512 с параметрами h, b, r равными 512, 1, 8 соответственно. Для улучшенного алгоритма количество попыток нужных для нахождения коллизии равно 2 ⁵²³ в сравнении со стандартным алгоритмом атаки с попытками для нахождения коллизии 2 ⁵³² . Если r = 8 , для улучшенного алгоритма нужно, чтобы b > 3 для того чтобы число попыток было меньше чем 2 ⁵¹² , для обычного алгоритма должно выполнятся условия b > 5 .

Атака на основе симметрии

Как было сказано выше, алгоритм CubeHash очень симметричен и в нём не используются какие-либо константы. Поэтому существует много классов симметрии относительно перестановок. Самый эффективный способ атаки — это использовать класс симметрии, для которого расширение сообщения может генерировать симметричные сообщения. Например, мы можем использовать класс симметрии называемый C2. Для этого класса состояние называется симметричным если x _ijkl0 =x _ijkl1 для любых i, j, k, l.

Когда параметр b равен 32, то есть CubeHash является нормальным, инъекция сообщения дает контроль над x _00klm для любых k, l, m.

Поэтому, для того чтобы достичь симметричного состояния нужно просто достичь состояния удовлетворяющему следующему 384-битному уравнения

x _01kl0 =x _01kl1

x _10kl0 =x _10kl1

x _11kl0 =x _11kl1

для любых k, l.

И тогда инъекция сообщения может быть использована для достижения полностью симметричного состояния. Ожидаемая сложность при этом 2 ³⁸⁴ .

Это может быть использовано для атаки нахождения прообраза. Алгоритм можно записать следующим образом

1. Найти сообщение А, которое будет симметрично с инициализирующим вектором
2. Найти сообщение D, которое симметрично в обратном порядке с заданным.
3. Сформировать 2 ¹⁹² симметричных сообщений B _j . Затем вычислить состояния, получающееся после выполнения операции или над A и B _j
4. Сформировать 2 ¹⁹² симметричных сообщений С _j . Затем вычислить состояния, получающееся после выполнения операции или над выполнения C _j и D.
5. С высокой вероятностью найдётся пара значений, удовлетворяющих

b _01kl0 =c _01kl0

b _10kl0 =c _10kl0

b _11kl0 =c _11kl0

тогда из симметрии следуют следующие равенства

b _01kl1 =c _01kl1

b _10kl1 =c _10kl1

b _11kl1 =c _11kl1

выполняющиеся для любых k, l.

Затем используем блок Х, чтобы сопоставить первые 256 бит. Это даёт прообраз — выполняем операцию или над A, B _{i 0} , X, C _{i 0} , D.

Сложность шагов 1 и 2 это 2 ³⁸⁴ , а сложность шагов 3 и 4 это 2 ¹⁹² . Он может быть реализован без больших затрат памяти. Эта атака имеет такую же сложность, как атака основанная на мощности, когда B является степенью двойки, но она становится эффективней когда b не является степенью двойки.

Наиболее трудоёмкая часть атаки, основанной на симметрии — это вычисления нужные для вычисления симметричного состояния. Тем не менее, оказывается, что эта задача легко решается с использованием алгоритма Гровера на квантовом компьютере. На самом деле нахождение состояния, удовлетворяющего уравнению, описанному выше, эквивалентно нахождению прообраза нуля для хеш функции, которая будет перебирать раунды функции CubeHash, и выход которой будет представлен

x ₀₁₀₀₀ ${\displaystyle \oplus _{2}}$ x ₀₁₀₀₁

x ₀₁₀₁₀ ${\displaystyle \oplus _{2}}$ x ₀₁₀₁₁

x ₀₁₁₀₀ ${\displaystyle \oplus _{2}}$ x ₀₁₁₀₁

x ₀₁₁₁₀ ${\displaystyle \oplus _{2}}$ x ₀₁₁₁₁

x ₁₀₀₀₀ ${\displaystyle \oplus _{2}}$ x ₁₀₀₀₁

x ₁₀₀₁₀ ${\displaystyle \oplus _{2}}$ x ₁₀₀₁₁

x ₁₀₁₀₀ ${\displaystyle \oplus _{2}}$ x ₁₀₁₀₁

x ₁₀₁₁₀ ${\displaystyle \oplus _{2}}$ x ₁₀₁₁₁

x ₁₁₀₀₀ ${\displaystyle \oplus _{2}}$ x ₁₁₀₀₁

x ₁₁₀₁₀ ${\displaystyle \oplus _{2}}$ x ₁₁₀₁₁

x ₁₁₁₀₀ ${\displaystyle \oplus _{2}}$ x ₁₁₁₀₁

x ₁₁₁₁₀ ${\displaystyle \oplus _{2}}$ x ₁₁₁₁₁

Для 384-битной функции алгоритм Гровера имеет сложность, равную 2 ¹⁹² операций. Тогда атака с использованием симметрии будет требовать 2 ¹⁹² операций при условии, что квантовые компьютеры являются доступными.

Примечания

Литература

• Eric Brier и Thomas Peyrin. Cryptanalysis of CubeHash // . — Springer-Verlag Berlin Heidelberg, 2009. — С. —368. — 535 с. — ISBN 978-3-642-01956-2 .

Ссылки

• (англ.)