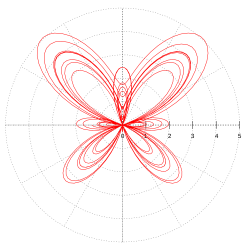
Параметрическое представление — используемая в математическом анализе разновидность представления переменных , когда их зависимость выражается через дополнительную величину — параметр.

Параметрическое представление функции

Предположим, что функциональная зависимость ${\displaystyle y}$ от ${\displaystyle x}$ задана не непосредственно как ${\displaystyle y=f(x),}$ а через промежуточную величину ${\displaystyle t.}$

Тогда формулы:

${\displaystyle x=\varphi (t);\ }$ ${\displaystyle y=\psi (t)}$

задают параметрическое представление функции одной переменной.

Если предположить, что обе эти функции ${\displaystyle \varphi }$ и ${\displaystyle \psi }$ имеют производные и для ${\displaystyle \varphi }$ существует обратная функция ${\displaystyle \theta ,}$ явное представление функции выражается через параметрическое как :

${\displaystyle y=\psi [\theta (x)]=f(x)}$

и производная функции ${\displaystyle y(x)}$ может быть вычислена как:

${\displaystyle y'(x)={\frac {dy}{dx}}={\frac {y'_{t}}{x'_{t}}}={\frac {\psi '(t)}{\varphi '(t)}}.}$

Параметрическое представление даёт такое важное преимущество, что позволяет изучать неявные функции в тех случаях, когда их приведение к явному виду иначе как через параметры затруднительно или невозможно через элементарные функции .

Параметрическое представление уравнения

Параметрическое представление для более общего случая: когда переменные связаны уравнением (или системы уравнений , если переменных больше двух).

Параметрическое уравнение

Близкое понятие — параметрическое уравнение множества точек, когда координаты точек задаются как функции от некоторого набора свободных параметров. Если параметр один, мы получим параметрическое уравнение кривой.

${\displaystyle x=x(t);y=y(t)}$ (кривая на плоскости),

${\displaystyle x=x(t);y=y(t);z=z(t)}$ (кривая в 3-мерном пространстве),

Выражая координаты точек поверхности через два свободных параметра, мы получим параметрическое задание поверхности .

Примеры

Уравнение окружности имеет вид:

${\displaystyle x^{2}+y^{2}=r^{2}.}$

Параметрическое уравнение окружности:

${\displaystyle x=r~\cos ~t~;}$ ${\displaystyle y=r~\sin ~t~;~~0\leq t<2\pi }$

Гипербола описывается следующим уравнением:

${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1.}$

Параметрическое уравнение правой ветви гиперболы :

${\displaystyle x=a~\operatorname {ch} ~t}$ ${\displaystyle ;~y=b~\operatorname {sh} ~t~;~~-\infty <t<+\infty }$

См. также

• Параметрическое задание поверхности

Примечания

Ссылки