Ограниченная машина Больцмана ( англ. restricted Boltzmann machine), сокращённо RBM — вид генеративной стохастической нейронной сети , которая определяет распределение вероятности на входных образцах данных.

Первая ограниченная машина Больцмана была построена в 1986 году Полом Смоленски под названием Harmonium , но приобрела популярность только после изобретения Хинтоном быстрых алгоритмов обучения в середине 2000-х годов.

Такое название машина приобрела как модификация обычной машины Больцмана , в которой нейроны разделили на видимые и скрытые, а связи допустимы только между нейронами разного типа, таким способом ограничив связи. Значительно позже, в 2000-х годах, ограниченные машины Больцмана приобрели большую популярность и стали рассматриваться уже не как вариации машины Больцмана, а как особые компоненты в архитектуре сетей глубинного обучения . Объединение нескольких каскадов ограниченных машин Больцмана формирует глубокую сеть доверия , особый вид многослойных нейронных сетей, которые могут самообучаться без учителя при помощи алгоритма обратного распространения ошибки .

Особенностью ограниченных машин Больцмана является возможность проходить обучение без учителя , но в определённых приложениях ограниченные машины Больцмана обучаются с учителем. Скрытый слой машины представляет собой глубокие признаки в данных, которые выявляются в процессе обучения (см. также Data mining ).

Ограниченные машины Больцмана имеют широкий спектр применений — это задачи снижения размерности данных , задачи классификации , коллаборативная фильтрация , выделение признаков ( англ. feature learning) и тематическое моделирование .

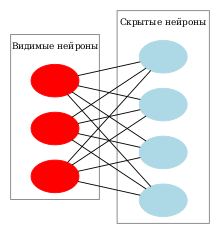
В ограниченной машине Больцмана нейроны образуют двудольный граф , с одной стороны графа находятся видимые нейроны (вход), а с другой стороны — скрытые, причём перекрёстные связи устанавливаются между каждым видимым и каждым скрытым нейроном. Такая система связей позволяет применить при обучении сети метод градиентного спуска с контрастивной дивергенцией .

Структура сети

Ограниченная машина Больцмана базируется на бинарных элементах с распределением Бернулли , составляющие видимый ${\displaystyle v_{i}}$ и скрытый ${\displaystyle h_{j}}$ слои сети. Связи между слоями задаются с помощью матрицы весов ${\displaystyle W=(w_{i,j})}$ (размера m × n ), а также смещений ${\displaystyle a_{i}}$ для видимого слоя и ${\displaystyle b_{j}}$ для скрытого слоя.

Вводится понятие энергии сети ( v , h ) как

${\displaystyle E(v,h)=-\sum _{i}a_{i}v_{i}-\sum _{j}b_{j}h_{j}-\sum _{i}\sum _{j}v_{i}w_{i,j}h_{j},}$

или в матричной форме

${\displaystyle E(v,h)=-a^{\mathrm {T} }v-b^{\mathrm {T} }h-v^{\mathrm {T} }Wh.}$

Подобной функцией энергии обладает также Сеть Хопфилда . Как и для обычной машины Больцмана , через энергию определяется вероятность распределения на векторах видимого и скрытого слоя :

${\displaystyle P(v,h)={\frac {1}{Z}}e^{-E(v,h)},}$

где ${\displaystyle Z}$ — статсумма , определяемая как ${\displaystyle \sum e^{-E(v,h)}}$ для всех возможных сетей (иными словами, ${\displaystyle Z}$ — константа нормализации, которая гарантирует, что сумма всех вероятностей равна единице). Определение вероятности для отдельного входного вектора (маргинальное распределение) проводится аналогично через сумму конфигураций всевозможных скрытых слоёв :

${\displaystyle P(v)={\frac {1}{Z}}\sum _{h}e^{-E(v,h)}.}$

По причине структуры сети как двудольного графа, отдельные элементы скрытого слоя независимы друг от друга и активируют видимый слой, и наоборот отдельные элементы видимого слоя независимы друг от друга и активируют скрытый слой . Для ${\displaystyle m}$ видимых элементов и для ${\displaystyle n}$ скрытых элементов условные вероятности v определяются через произведения вероятностей h :

${\displaystyle P(v|h)=\prod _{i=1}^{m}P(v_{i}|h),}$

и наоборот условные вероятности h определяются через произведение вероятностей v :

${\displaystyle P(h|v)=\prod _{j=1}^{n}P(h_{j}|v).}$

Конкретные вероятности активации для одного элемента определяются как

${\displaystyle P(h_{j}=1|v)=\sigma \left(b_{j}+\sum _{i=1}^{m}w_{i,j}v_{i}\right)}$ и ${\displaystyle P(v_{i}=1|h)=\sigma \left(a_{i}+\sum _{j=1}^{n}w_{i,j}h_{j}\right),}$

где ${\displaystyle \sigma }$ — логистическая функция для активации слоя.

Видимые слои могут иметь также мультиномиальное распределение , в то время как скрытые слои распределены по Бернулли . В случае мультиномиальности вместо логистической функции используется softmax :

${\displaystyle P(v_{i}^{k}=1|h)={\frac {\exp(a_{i}^{k}+\Sigma _{j}W_{ij}^{k}h_{j})}{\Sigma _{k'=1}^{K}\exp(a_{i}^{k'}+\Sigma _{j}W_{ij}^{k'}h_{j})}},}$

где K — количество дискретных значений видимых элементов. Такое представление используется в задачах тематического моделирования и в рекомендательных системах .

Связь с другими моделями

Ограниченная машина Больцмана представляет собой частный случай обычной машины Больцмана и марковской сети . Их графовая модель соответствует графовой модели факторного анализа .

Алгоритм обучения

Целью обучения является максимизация вероятности системы с заданным набором образцов ${\displaystyle V}$ (матрицы, в которой каждая строка соответствует одному образцу видимого вектора ${\displaystyle v}$ ), определяемой как произведение вероятностей

${\displaystyle \arg \max _{W}\prod _{v\in V}P(v),}$

или же, что одно и то же, максимизации логарифма произведения:

${\displaystyle \arg \max _{W}\mathbb {E} [\log P(v)].}$

Для тренировки нейронной сети используется алгоритм контрастивной дивергенции (CD) с целью нахождения оптимальных весов матрицы ${\displaystyle W}$ , его предложил Джеффри Хинтон , первоначально для обучения моделей PoE («произведение экспертных оценок») . Алгоритм использует семплирование по Гиббсу для организации процедуры градиентного спуска , аналогично методу обратного распространения ошибок для нейронных сетей.

В целом один шаг контрастивной дивергенции (CD-1) выглядит следующим образом:

1. Для одного образца данных v вычисляются вероятности скрытых элементов и применяется активация для скрытого слоя h для данного распределения вероятностей.
2. Вычисляется внешнее произведение (семплирование) для v и h , которое называют позитивным градиентом .
3. Через образец h проводится реконструкция образца видимого слоя v' , а потом выполняется снова семплирование с активацией скрытого слоя h' . (Этот шаг называется Семплирование по Гиббсу .)
4. Далее вычисляется внешнее произведение , но уже векторов v' и h' , которое называют негативным градиентом .
5. Матрица весов ${\displaystyle W}$ поправляется на разность позитивного и негативного градиента, помноженного на множитель, задающий скорость обучения: ${\displaystyle \Delta W=\varepsilon (vh^{\mathsf {T}}-v'h'^{\mathsf {T}})}$ .
6. Вносятся поправки в биасы a и b похожим способом: ${\displaystyle \Delta a=\varepsilon (v-v')}$ , ${\displaystyle \Delta b=\varepsilon (h-h')}$ .

Практические указания по реализации процесса обучения можно найти на личной странице Джеффри Хинтона .

См. также

• Автокодировщик
• Глубокое обучение
• Сеть Хопфилда

Ссылки

Литература

• от 29 октября 2012 на Wayback Machine . Edwin Chen’s blog, July 18, 2011.
• . Deeplearning4j Documentation
• . Deeplearning4j Documentation, August 4, 2015.
• Python от 5 марта 2017 на Wayback Machine of Bernoulli RBM and от 5 марта 2017 на Wayback Machine
• от 10 июня 2018 на Wayback Machine is a very small RBM code (24kB) useful for you to learn about how RBMs learn.