Interested Article - Ломаная

Ло́маная (ло́маная ли́ния) — геометрическая фигура на плоскости, образованная конечным набором отрезков , расположенных так, что конец первого является началом второго, конец второго — началом третьего и т. д.; причём соседние отрезки не должны лежать на одной прямой.

Сами отрезки называются сторонами ломаной, а их концы — вершинами ломаной. Ломаная обозначается последовательным указанием её вершин.

Определение

Ломаной $A_{1}A_{2}\dots A_{n}$ $A_{1}A_{2}\dots A_{n}$ называется фигура, которая состоит из отрезков $[A_{1}A_{2}]$ $[A_{1}A_{2}]$ , $[A_{2}A_{3}]$ $[A_{2}A_{3}]$ , …, $[A_{n-1}A_{n}]$ $[A_{{n-1}}A_{n}]$ .

Точки $A_{1}$ $A_{1}$ , … $A_{n}$ $A_{{n}}$ , называются вершинами ломаной, а отрезки $[A_{1}A_{2}]$ $[A_{1}A_{2}]$ , $[A_{2}A_{3}]$ $[A_{2}A_{3}]$ , …, $[A_{n-1}A_{n}]$ $[A_{{n-1}}A_{n}]$ — сторонами (звеньями) ломаной.

Ломаная называется невырожденной , если для любого $k\in \{1,2,\dots ,n-2\}$ $k\in \{1,2,\dots ,n-2\}$ отрезки $[A_{k}A_{k+1}]$ $[A_{k}A_{{k+1}}]$ и $[A_{k+1}A_{k+2}]$ $[A_{{k+1}}A_{{k+2}}]$ не лежат на одной прямой ; ^{[

источник не указан 229 дней

]} в противном случае — вырожденной . ^{[

источник не указан 229 дней

]}

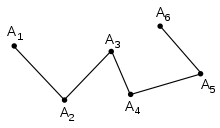
Невырожденная ломаная A ₁ A ₂ A ₃ A ₄ A ₅ A ₆

Типы ломаных

Ломаная имеет самопересечение , если хотя бы два её несмежных звена имеют общую точку:

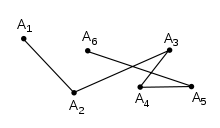
Ломаная с самопересечениями — Самопересекающаяся ломаная A ₁ A ₂ A ₃ A ₄ A ₅ A ₆

Изображённую здесь ломаную следует называть «ломаная A ₁ A ₂ A ₃ A ₄ A ₅ A ₆ ».

Ломаная называется замкнутой , если первая и последняя точки ломаной совпадают; в этом случае дополнительно требуют, чтобы отрезки $A_{1}A_{2}$ $A_{1}A_{2}$ и $A_{n-1}A_{n}$ $A_{{n-1}}A_{n}$ также не лежали на одной прямой:

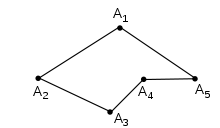
Замкнутая ломаная A ₁ A ₂ A ₃ A ₄ A ₅ A ₁

Замкнутую плоскую ломаную часто называют многоугольником : в этом случае изображённая ломаная A ₁ A ₂ A ₃ A ₄ A ₅ A ₁ будет называться «многоугольник A ₁ A ₂ A ₃ A ₄ A ₅ A ₁ », а звенья будут называться сторонами многоугольника. В ряде случаев, например, при рассмотрении многогранников , стороны многоугольника называются рёбрами .