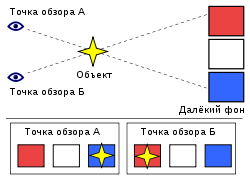
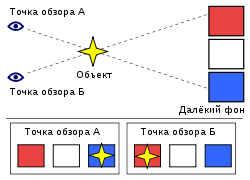
Паралла́кс ( греч. παράλλαξις , от παραλλαγή , «смена, чередование») — изменение видимого положения объекта относительно удалённого фона в зависимости от положения наблюдателя.

Зная расстояние между точками наблюдения L ( базис ) и угол смещения α, можно определить расстояние до объекта:

${\displaystyle D={\frac {L}{2\sin \alpha /2}}.}$

Для малых углов (α — в радианах )

${\displaystyle D={\frac {L}{\alpha }}.}$

Параллакс используется в геодезии и астрономии для измерения расстояния до удалённых объектов (в частности в специальных единицах — парсеках ). На явлении параллакса основано бинокулярное зрение .

Астрономия

Суточный параллакс

Суточный параллакс (геоцентрический параллакс) — разница в направлениях на одно и то же светило из центра масс Земли (геоцентрическое направление) и из заданной точки на поверхности Земли (топоцентрическое направление).

Этот угол зависит от высоты светила над горизонтом, максимальное его значение достигается при нулевой высоте (когда светило наблюдается прямо на горизонте). Такая величина называется горизонтальным параллаксом . База параллакса при этом равна радиусу Земли (около 6400 км).

Из-за вращения Земли вокруг своей оси положение наблюдателя относительно центра Земли и, соответственно, параллактический угол циклически изменяются.

При наблюдении Луны её кажущиеся смещения на фоне звёзд (по сравнению с расчётным орбитальным движением) достигают 2° (соответственно, параллакс равен 1°) и были замечены уже древнегреческими астрономами, что позволило им довольно точно определить расстояние до Луны .

Суточный параллакс планет довольно мал (для Марса 24″ во время великого противостояния ), но тем не менее был единственным способом измерения абсолютных расстояний в Солнечной системе до появления радиолокации : наиболее удобными для этого были прохождения Венеры по диску Солнца и близко подходящие к Земле астероиды (относительные же расстояния легко определяются на основе законов Кеплера , так что достаточно абсолютного измерения какого-то одного расстояния, чтобы определить все).

Годичный параллакс

Годичный параллакс — изменение направления на объект (например, звезду), связанное с движением Земли вокруг Солнца. Величина параллакса равна углу, под которым со звезды видна большая полуось земной орбиты (перпендикулярная лучу зрения).

Годичные параллаксы являются показателями расстояний до звёзд. Расстояние до объекта, годичный параллакс которого равен 1 угловой секунде , называется парсек (1 парсек = 3,085678⋅10 ¹⁶ м). Ближайшая к нам звезда Проксима Центавра имеет параллакс 0,7687±0,0003″, следовательно, расстояние до неё составляет 1,3009±0,00015 пк.

Вековой параллакс

Вековым параллаксом обычно называется изменение видимого положения объекта на небесной сфере в результате комбинаций собственных движений этого объекта и Солнечной системы в галактике .

Параллакс в фотографии

Параллакс видоискателя

Параллакс видоискателя — несовпадение границ изображения, видимых в оптическом видоискателе, с границами изображения, получаемого в кадровом окне . Параллакс почти незаметен в случае съёмки удалённых объектов, и весьма значителен на небольших конечных дистанциях . Он возникает из-за наличия расстояния (базиса) между оптическими осями съёмочного объектива и видоискателя. Величина параллакса ${\displaystyle P}$ определяется по формуле

${\displaystyle P=B{\frac {f}{R}},}$

где ${\displaystyle B}$ — расстояние (базис) между оптическими осями объектива и видоискателя, ${\displaystyle f}$ — фокусное расстояние объектива фотоаппарата, ${\displaystyle R}$ — расстояние до плоскости наводки (объекта съёмки). От параллакса полностью свободны сквозные визиры однообъективных зеркальных фотоаппаратов , кинокамер с зеркальным обтюратором , а также псевдозеркальных и беззеркальных цифровых фотоаппаратов .

Параллакс прицела

Частным случаем является параллакс прицела . Параллакс прицела — это угол между осью ствола и осью прицела с вершиной на цели. Чем ближе цель к стрелку, тем больше этот угол, тем больше надо корректировать прицел. Если прицел пристрелян на расстояние в 100 метров, а цель находится на расстоянии 50 метров, то пуля пролетит ниже цели. И чем ближе цель будет приближаться к 100 метрам от стрелка, тем ближе будет попадание к цели. При нахождении цели дальше 100 метров пуля пролетит выше цели. Баллистика в данном вопросе не учитывается.

Параллакс дальномера

Параллакс дальномера — угол, под которым виден объект во время наводки на резкость с помощью оптического дальномера.

Стереоскопический параллакс

Стереоскопический (бинокулярный) параллакс — это угол, под которым рассматривают объект двумя глазами или когда его фотографируют стереоскопическим фотоаппаратом .

Временно́й параллакс

Временной параллакс — искажение формы быстро движущихся объектов, возникающее при съёмке фотоаппаратом со шторно-щелевым фокальным затвором или видеокамерой со строчным переносом. Так как экспозиция происходит не единовременно по всей площади светочувствительного элемента, а последовательно по мере движения щели, то при съёмке быстро движущихся объектов их форма может искажаться. Например, если объект движется в ту же сторону, что и щель затвора, его изображение будет растянуто, а если в обратную, то сужено.

Примечания

Литература

• Бунимович Д. З. / Е. А. Иофис . — М. : «Искусство», 1962. — 128 с.
• Иофис Е. А. Техника фотографии. — М. : «Искусство», 1973. — 349 с.
• Яштолд-Говорко В. А. Фотосъёмка и обработка. Съёмка, формулы, термины, рецепты. Изд. 4-е, сокр. — М.: «Искусство», 1977.
• Hirshfeld, Alan w. . — New York: (англ.) (, 2001. — ISBN 978-0-7167-3711-7 .
• Whipple, Fred L. Earth Moon and Planets. — Read Books, 2007. — ISBN 978-1-4067-6413-0 .
• Zeilik, Michael A.; Gregory, Stephan A. . — 4th. — (англ.) (, 1998. — ISBN 978-0-03-006228-5 .

Ссылки

• — обзор об измерении расстояний до астрономических объектов (англ.)