Дискретная версия теоремы Грина описывает отношение между двойным интегралом функции для обобщенной прямоугольной области (область, которая образуется из конечного суммирования прямоугольников на плоскости) и линейной комбинации первообразной функции , заданной в углах области. В этом значении мы будем рассматривать дискретной теоремы Грина.

Теорема названа в честь британского математика Джорджа Грина , из-за сходства с его теоремой, теоремой Грина: обе теоремы описывают связь между интегрированием по кривой и интегрированием по области, ограниченной кривой. Теорема была впервые представлена как непрерывное продолжение алгоритма Ванга «Интегральное представление изображений», в 2007 году на Международной конференции по компьютерному видению ICCV , а затем вновь была опубликована профессором Doretto и его коллегами в рецензируемом журнале в 2011 году.

Формулировка

Предположим что ƒ является интегрируемой функцией на плоскости R ² , так что:

${\displaystyle F\left(x,y\right)\equiv \int _{0}^{y}\int _{0}^{x}f\left(u,v\right)\,du\,dv}$

является её первообразной функцией . Пусть ${\displaystyle D\subset R^{2}}$ — обобщенная прямоугольная область. Тогда представим теорему как:

${\displaystyle \iint _{D}f\left(x,y\right)\,dx\,dy=\sum _{{\vec {x}}\in \nabla \cdot D}\alpha _{D}\left({\vec {x}}\right)\cdot F\left({\vec {x}}\right),}$

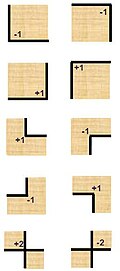
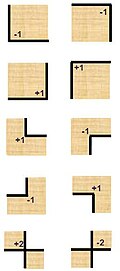
где ${\displaystyle \nabla \cdot D}$ — множество углов данной области D , ${\displaystyle \alpha _{D}}$ является дискретным параметром с возможными значениями {0, ±1, ±2}, которые определяются в зависимости от типа угла, как показано на рисунке справа. Этот параметр является частным случаем стремления кривой , которая последовательно определяется при помощи одностороннего разрыва кривой в углах заданной области.

Эта теорема является естественным продолжением алгоритма таблицы обобщённой области. Эта теорема расширяет алгоритм в том смысле, что область может быть непрерывной и она может быть сформирована из (конечного) числа прямоугольников, тогда как в алгоритме таблицы обобщённой области предполагается, что область является единым прямоугольником.

Дискретная теорема Грина также обобщает теорему Ньютона-Лейбница .

Идея доказательства

Для доказательства теоремы можно применить формулу из алгоритма "Интегрального представление изображений", которая включает в себя прямоугольники, образующие данную область:

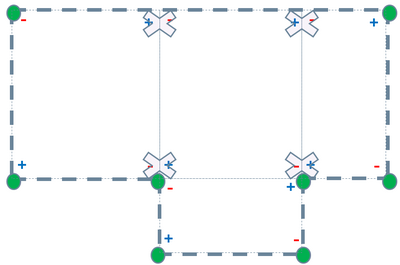
Это изображение показывает, как + \ — коэффициенты первоначальной функции взаимно сокращаются в прямоугольниках, кроме точек расположенных в углах данной области.

Пример

Предположим что функция ƒ , задана на плоскости R ² , тогда F является её первообразной функцией. Пусть D — это область, окрашенная зелёным на следующем рисунке:

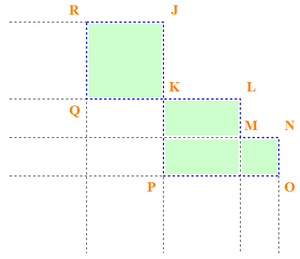
Согласно теореме, примененимой к данной области, получается следующее выражение:

${\displaystyle \iint _{D}f\left(x,y\right)\,dx\,dy=F\left(J\right)-2F\left(K\right)+F\left(L\right)-F\left(M\right)+F\left(N\right)-F\left(O\right)+F\left(P\right)+F\left(Q\right)-F\left(R\right).}$

Приложения

Дискретная теорема Грина используется в компьютерных приложениях по обнаружению объектов на изображениях и их быстрого вычисления, а также в интересах эффективного расчета вероятностей.

Обобщения

В 2011 году были предложены два обобщения к теореме:

• Подход, предложенный профессором Фам и его коллегами: обобщение теоремы полигональных областей с помощью динамического программирования .
• Подход, предложенный математиком Шахар: обобщение теоремы на более широкий спектр областей при помощью оператора разрыва и метода интегрирования наклонной линии при помощи которых и была сформулирована дискретная теорема Грина .

Видео лекции

• .

См. также

• Теорема Грина

Примечания