ГОСТ 34.10-2018 (полное название: « ГОСТ 34.10-2018. Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи », англ. « Information technology. Cryptographic data security. Signature and verification processes of electronic digital signature ») — действующий межгосударственный криптографический стандарт , описывающий алгоритмы формирования и проверки электронной цифровой подписи реализуемой с использованием операций в группе точек эллиптической кривой, определенной над конечным простым полем.

Стандарт разработан на основе национального стандарта Российской Федерации ГОСТ Р 34.10-2012 и введен в действие с 1 июня 2019 года приказом Росстандарта № 1059-ст от 4 декабря 2018 года .

Область применения

Цифровая подпись позволяет:

1. Аутентифицировать лицо, подписавшее сообщение;
2. Контролировать целостность сообщения;
3. Защищать сообщение от подделок;

История

Первые версии алгоритма разрабатывались Главным управлением безопасности связи ФАПСИ при участии , позже разработка перешла в руки Центра защиты информации и специальной связи ФСБ России и АО «ИнфоТеКС» .

Описание

Криптографическая стойкость первых стандартов цифровой подписи ГОСТ Р 34.10-94 и ГОСТ 34.310-95 была основана на задаче дискретного логарифмирования в мультипликативной группе простого конечного поля большого порядка. Начиная с ГОСТ Р 34.10-2001 стойкость алгоритма основана на более сложной задаче вычисления дискретного логарифма в группе точек эллиптической кривой . Также стойкость алгоритма формирования цифровой подписи основана на стойкости соответствующей хеш-функции:

Тип	Наименование	Введен в действие	Функция хеширования	Приказ
Национальный	ГОСТ Р 34.10-94	1 января 1995 года	ГОСТ Р 34.11-94	Принят постановлением Госстандарта России № 154 от 23 мая 1994 года
Межгосударственный	ГОСТ 34.310-95	16 апреля 1998 года	ГОСТ 34.311-95
Национальный	ГОСТ Р 34.10-2001	1 июля 2002 года	ГОСТ Р 34.11-94	Принят постановлением Госстандарта России № 380-ст от 12 сентября 2001 года
Межгосударственный	ГОСТ 34.310-2004	2 марта 2004 года	ГОСТ 34.311-95	Принят Евразийским советом по стандартизации, метрологии и сертификации по переписке (протокол № 16 от 2 марта 2004 года)
Национальный	ГОСТ Р 34.10-2012	1 января 2013 года	ГОСТ Р 34.11-2012	Утверждён и введен в действие приказом Федерального агентства по техническому регулированию и метрологии № 215-ст от 7 августа 2012 года в качестве национального стандарта Российской Федерации с 1 января 2013 года
Межгосударственный	ГОСТ 34.10-2018	1 июня 2019 года	ГОСТ 34.11-2018	Принят Межгосударственным советом по метрологии, стандартизации и сертификации (протокол № 54 от 29 ноября 2018 года). Приказом Федерального агентства по техническому регулированию и метрологии № 1059-ст от 4 декабря 2018 г. введен в действие в качестве национального стандарта Российской Федерации с 1 июня 2019 года

Стандарты используют одинаковую схему формирования электронной цифровой подписи. Новые стандарты с 2012 года отличаются наличием дополнительного варианта параметров схем, соответствующего длине секретного ключа порядка 512 бит.

После подписывания сообщения М к нему дописывается цифровая подпись размером 512 или 1024 бит , и текстовое поле. В текстовом поле могут содержаться, например, дата и время отправки или различные данные об отправителе:

Сообщение М	+	Цифровая подпись Текст
		Дополнение

Данный алгоритм не описывает механизм генерации параметров, необходимых для формирования подписи, а только определяет, каким образом на основании таких параметров получить цифровую подпись. Механизм генерации параметров определяется на месте в зависимости от разрабатываемой системы.

Алгоритм

Приводится описание варианта схемы ЭЦП с длиной секретного ключа 256 бит. Для секретных ключей длиной 512 бит (второй вариант формирования ЭЦП, описанный в стандарте) все преобразования аналогичны.

Параметры схемы цифровой подписи

• простое число ${\displaystyle p}$ — модуль эллиптической кривой такой, что ${\displaystyle p>2^{255}}$
• эллиптическая кривая ${\displaystyle E}$ задаётся своим инвариантом ${\displaystyle J(E)}$ или коэффициентами ${\displaystyle a,b\in F_{p}}$ , где ${\displaystyle F_{p}}$ — конечное поле из p элементов. ${\displaystyle J(E)}$ связан с коэффициентами ${\displaystyle a}$ и ${\displaystyle b}$ следующим образом

${\displaystyle J(E)=1728{\frac {4a^{3}}{4a^{3}+27b^{2}}}{\pmod {p}}}$ , причём ${\displaystyle 4a^{3}+27b^{2}\not \equiv 0{\pmod {p}}}$ .

• целое число ${\displaystyle m}$ — порядок группы точек эллиптической кривой, ${\displaystyle m}$ должно быть отлично от ${\displaystyle p}$
• простое число ${\displaystyle q}$ , порядок некоторой циклической подгруппы группы точек эллиптической кривой, то есть выполняется ${\displaystyle m=nq}$ , для некоторого ${\displaystyle n\in \mathbb {N} }$ . Также ${\displaystyle q}$ лежит в пределах ${\displaystyle 2^{254}<q<2^{256}}$ .
• точка ${\displaystyle P=(x_{P},\;y_{P})}$ эллиптической кривой ${\displaystyle E}$ , являющаяся генератором подгруппы порядка ${\displaystyle q}$ , то есть ${\displaystyle q\cdot P=\mathbf {0} }$ и ${\displaystyle k\cdot P\neq \mathbf {0} }$ для всех k = 1, 2, …, q -1, где ${\displaystyle \mathbf {0} }$ — нейтральный элемент группы точек эллиптической кривой E .
• ${\displaystyle h(M)}$ — хеш-функция ( ГОСТ Р 34.11-2012 ), которая отображает сообщения M в двоичные векторы длины 256 бит.

Каждый пользователь цифровой подписи имеет личные ключи:

• ключ шифрования ${\displaystyle d}$ — целое число, лежащее в пределах ${\displaystyle 0<d<q}$ .
• ключ расшифрования ${\displaystyle Q=(x_{Q},\;y_{Q})}$ , вычисляемый как ${\displaystyle Q=d\cdot P}$ .

Дополнительные требования:

• ${\displaystyle p^{t}\neq 1{\pmod {q}}}$ , ${\displaystyle \forall t=1..B}$ , где ${\displaystyle B\geq 31}$
• ${\displaystyle J(E)\neq 0}$ и ${\displaystyle J(E)\neq 1728}$

Двоичные векторы

Между двоичными векторами длины 256 ${\displaystyle {\bar {h}}=(\alpha _{255},...,\alpha _{0})}$ и целыми числами ${\displaystyle z\leq 2^{256}}$ ставится взаимно-однозначное соответствие по следующему правилу ${\displaystyle z=\sum _{i=0}^{255}\alpha _{i}2^{i}}$ . Здесь ${\displaystyle \alpha _{i}}$ либо равно 0, либо равно 1. Другими словами, ${\displaystyle {\bar {h}}}$ — это представление числа z в двоичной системе счисления.

Результатом операции конкатенации двух векторов ${\displaystyle {\bar {h_{1}}}=(\alpha _{255},...,\alpha _{0})}$ и ${\displaystyle {\bar {h_{2}}}=(\beta _{255},...,\beta _{0})}$ называется вектор длины 512 ${\displaystyle ({\bar {h_{1}}}|{\bar {h_{2}}})=(\alpha _{255},...,\alpha _{0},\beta _{255},...,\beta _{0})}$ . Обратная операция — операция разбиения одного вектора длины 512 на два вектора длины 256.

Формирование цифровой подписи

Блок-схемы :

• 
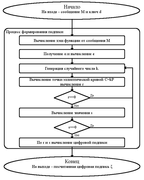  Формирование цифровой подписи
• 
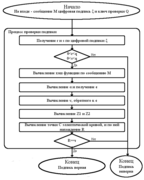  Проверка цифровой подписи

1. Вычисление хеш-функции от сообщения М: ${\displaystyle {\bar {h}}=h(M)}$
2. Вычисление ${\displaystyle e=z\,{\bmod {\,}}q}$ , и если ${\displaystyle e=0}$ , положить ${\displaystyle e=1}$ . Где ${\displaystyle z}$ — целое число, соответствующее ${\displaystyle {\bar {h}}.}$
3. Генерация случайного числа ${\displaystyle k}$ такого, что ${\displaystyle 0<k<q.}$
4. Вычисление точки эллиптической кривой ${\displaystyle C=kP}$ , и по ней нахождение ${\displaystyle r=x_{c}\,{\bmod {\,}}q,}$ где ${\displaystyle x_{c}}$ — это координата ${\displaystyle x}$ точки ${\displaystyle C.}$ Если ${\displaystyle r=0}$ , возвращаемся к предыдущему шагу.
5. Нахождение ${\displaystyle s=(rd+ke)\,{\bmod {\,}}q}$ . Если ${\displaystyle s=0}$ , возвращаемся к шагу 3.
6. Формирование цифровой подписи ${\displaystyle \xi =({\bar {r}}|{\bar {s}})}$ , где ${\displaystyle {\bar {r}}}$ и ${\displaystyle {\bar {s}}}$ — векторы, соответствующие ${\displaystyle r}$ и ${\displaystyle s}$ .

Проверка цифровой подписи

1. Вычисление по цифровой подписи ${\displaystyle \xi }$ чисел ${\displaystyle r}$ и ${\displaystyle s}$ , учитывая, что ${\displaystyle \xi =({\bar {r}}|{\bar {s}})}$ , где ${\displaystyle r}$ и ${\displaystyle s}$ — числа, соответствующие векторам ${\displaystyle {\bar {r}}}$ и ${\displaystyle {\bar {s}}}$ . Если хотя бы одно из неравенств ${\displaystyle r<q}$ и ${\displaystyle s<q}$ неверно, то подпись неправильная.
2. Вычисление хеш-функции от сообщения М: ${\displaystyle {\bar {h}}=h(M).}$
3. Вычисление ${\displaystyle e=z\,{\bmod {\,}}q}$ , и если ${\displaystyle e=0}$ , положить ${\displaystyle e=1}$ . Где ${\displaystyle z}$ — целое число соответствующее ${\displaystyle {\bar {h}}.}$
4. Вычисление ${\displaystyle \nu =e^{-1}\,{\bmod {\,}}q.}$
5. Вычисление ${\displaystyle z_{1}=s\nu \,{\bmod {\,}}q}$ и ${\displaystyle z_{2}=-r\nu \,{\bmod {\,}}q.}$
6. Вычисление точки эллиптической кривой ${\displaystyle C=z_{1}P+z_{2}Q}$ . И определение ${\displaystyle R=x_{c}\,{\bmod {\,}}q}$ , где ${\displaystyle x_{c}}$ — координата ${\displaystyle x}$ точки ${\displaystyle C.}$
7. В случае равенства ${\displaystyle R=r}$ подпись правильная, иначе — неправильная.

Криптостойкость

Криптостойкость цифровой подписи опирается на две компоненты — на стойкость хеш-функции и на стойкость самого алгоритма шифрования.

Вероятность взлома хеш-функции по ГОСТ 34.11-94 составляет ${\displaystyle 1{,}73\times {10}^{-77}}$ при подборе коллизии на фиксированное сообщение и ${\displaystyle 2{,}94\times {10}^{-39}}$ при подборе любой коллизии. Стойкость алгоритма шифрования основывается на проблеме дискретного логарифмирования в группе точек эллиптической кривой. На данный момент нет метода решения данной проблемы хотя бы с субэкспоненциальной сложностью.

Один из самых быстрых алгоритмов, на данный момент, при правильном выборе параметров — ${\displaystyle \rho }$ -метод и ${\displaystyle \mathrm {I} }$ -метод Полларда.

Для оптимизированного ${\displaystyle \rho }$ -метода Полларда вычислительная сложность оценивается как ${\displaystyle O({\sqrt {q}})}$ . Таким образом для обеспечения криптостойкости ${\displaystyle {10}^{30}}$ операций необходимо использовать 256-разрядное ${\displaystyle q}$ .

Отличия от ГОСТ Р 34.10-94 (стандарт 1994—2001 гг)

Новый и старый ГОСТы цифровой подписи очень похожи друг на друга. Основное отличие — в старом стандарте часть операций проводится над полем Z p {\displaystyle \mathbb {Z} _{p}} , а в новом — над группой точек эллиптической кривой, поэтому требования, налагаемые на простое число ${\displaystyle p}$ в старом стандарте ( ${\displaystyle 2^{509}<p<2^{512}}$ или ${\displaystyle 2^{1020}<p<2^{1024}}$ ), более жёсткие, чем в новом.

Алгоритм формирования подписи отличается только в . В старом стандарте в этом пункте вычисляются ${\displaystyle {\tilde {r}}=a^{k}\,{\bmod {\,}}p}$ и ${\displaystyle r={\tilde {r}}\,{\bmod {\,}}q}$ и, если ${\displaystyle r=0}$ , возвращаемся к пункту 3. Где ${\displaystyle 1<a<p-1}$ и ${\displaystyle a^{q}{\bmod {\,}}p=1}$ .

Алгоритм проверки подписи отличается только в . В старом стандарте в этом пункте вычисляется ${\displaystyle R=(a^{z_{1}}y^{z_{2}}\,{\bmod {\,}}p)\,{\bmod {\,}}q}$ , где ${\displaystyle y}$ — открытый ключ для проверки подписи, ${\displaystyle y=a^{d}\,{\bmod {\,}}p}$ . Если ${\displaystyle R=r}$ , подпись правильная, иначе неправильная. Здесь ${\displaystyle q}$ — простое число, ${\displaystyle 2^{254}<q<2^{256}}$ и ${\displaystyle q}$ является делителем ${\displaystyle p-1}$ .

Использование математического аппарата группы точек эллиптической кривой позволяет существенно сократить порядок модуля ${\displaystyle p}$ без потери криптостойкости.

Также старый стандарт описывает механизмы получения чисел ${\displaystyle p}$ , ${\displaystyle q}$ и ${\displaystyle a}$ .

Возможные применения

• Использование пары ключей (открытый, закрытый) для установления ключа сессии.
• Использование в сертификатах открытых ключей.
• Использование в S/MIME ( PKCS #7 , Cryptographic Message Syntax ).
• Использование для защиты соединений в TLS ( SSL , HTTPS , WEB ).
• Использование для защиты сообщений в ( XML Encryption ).
• Защита целостности Интернет-адресов и имён ( DNSSEC ).

Примечания

Ссылки

• Текст стандарта «Информационная технология. Криптографическая защита информации. Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма»
• Текст стандарта «Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи»
• Текст стандарта «Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи»
• Текст стандарта «Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи»

Программные реализации

• (неопр.) . — криптографический проект компании ООО «Криптоком» по добавлению российских криптографических алгоритмов в библиотеку OpenSSL .
• на сайте GitHub
• КриптоПро CSP — криптографический проект компании «Крипто-Про».
• (неопр.) . — криптографический проект компании ЗАО «Сигнал-КОМ» .
• (неопр.) . — кроссплатформенная криптографическая библиотека компании ООО «ЛИССИ» .
• (неопр.) . — программные комплексы, средства криптографической защиты информации компании ОАО «ИнфоТеКС» .
• на сайте GitHub
• Bouncy Castle

Аппаратные реализации

• Рутокен ЭЦП 2.0
• JaCarta-2 ГОСТ
• (неопр.) . Архивировано из 15 июля 2017 года.
• (неопр.) . Архивировано из 27 декабря 2017 года.