Молекуля́рно-кинети́ческая тео́рия ( МКТ ) — теория, созданная в XIX в., рассматривающая строение вещества, в основном газов, с точки зрения трёх основных приближённо верных положений:

• все тела состоят из частиц: атомов , молекул и ионов ;
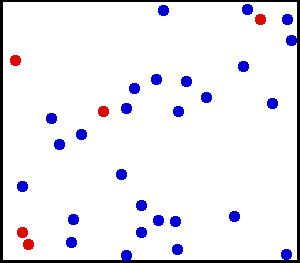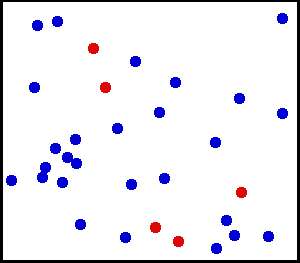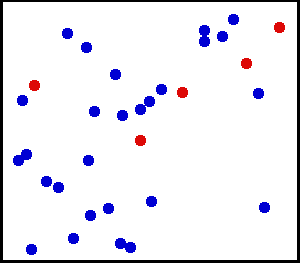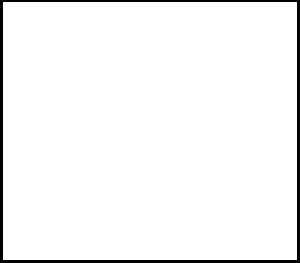
• частицы находятся в непрерывном хаотическом движении (тепловом);
• частицы взаимодействуют друг с другом путём абсолютно упругих столкновений .

МКТ стала одной из самых успешных физических теорий и была подтверждена многочисленными опытными фактами. Главным доказательством состоятельности МКТ явилось объяснение на её основе таких явлений как диффузия , броуновское движение и изменение агрегатных состояний вещества.

На базе МКТ развит ряд разделов современной физики, в частности, физическая кинетика и статистическая механика . В этих разделах изучаются не только молекулярные (атомные или ионные) системы, находящиеся не только в «тепловом» движении, и взаимодействующие не только через абсолютно упругие столкновения. Термин же молекулярно-кинетическая теория в современной теоретической физике уже практически не используется, хотя он встречается в учебниках по курсу общей физики.

История теории

Началом становления МКТ послужила теория М. В. Ломоносова . Ломоносов опытным путём опроверг теории о теплороде и флогистоне , подготовив тем самым, молекулярно-кинетическую теорию XIX века Рудольфа Клаузиуса , Людвига Больцмана и Джеймса Максвелла .

Основное уравнение МКТ

Основное уравнение МКТ имеет вид

${\displaystyle P={\frac {1}{3}}mn{\overline {v^{2}}}}$ .

Оно связывает макроскопические параметры (такие как давление ${\displaystyle P}$ , объём ${\displaystyle V}$ , температура ${\displaystyle T}$ ) газа с микроскопическими (масса частиц, средняя скорость их движения). В приведённой формуле ${\displaystyle m}$ — масса одной молекулы газа, ${\displaystyle n}$ (м ^-3 ) — концентрация молекул, ${\displaystyle {\overline {v^{2}}}}$ — средний квадрат скорости молекул. Уравнение может быть переписано так, чтобы ${\displaystyle V}$ и ${\displaystyle T}$ в него входили явно.

Релятивистское выражение для этой формулы

${\displaystyle P={\frac {2\rho c^{2}}{3}}\left((1-{\overline {v^{2}}}/c^{2})^{-1/2}-1\right)}$ ,

где ${\displaystyle \rho =mn}$ — плотность движущегося вещества, ${\displaystyle c}$ — скорость света . В пределе малых скоростей выражение превращается в ${\displaystyle P\approx \rho {\overline {v^{2}}}/3}$ .

Вывод основного уравнения

Пусть имеется кубический сосуд с ребром длиной ${\displaystyle L}$ и одна частица массой ${\displaystyle m}$ в нём. Введя координатные оси так, чтобы они были параллельны рёбрам куба, рассмотрим движение частицы вдоль оси ${\displaystyle x}$ и соударения с одной из граней (стенок), параллельных плоскости ${\displaystyle yz}$ .

Обозначим компоненту скорости движения вдоль оси ${\displaystyle x}$ через ${\displaystyle v_{x}}$ . Модуль этой компоненты неизменен всё время, но знак меняется при соударениях со стенкой. ${\displaystyle x}$ -составляющая импульса частицы до её столкновения со стенкой равна ${\displaystyle mv_{x}}$ , а после столкновения ${\displaystyle -mv_{x}}$ , поэтому стенке передаётся импульс

${\displaystyle \Delta p=2m|v_{x}|}$ .

Время, через которое частица сталкивается с одной и той же стенкой:

${\displaystyle \Delta t={\frac {2L}{|v_{x}|}}}$ .

Сила, действующая со стороны частицы на стенку, равна нулю всё время, кроме момента удара, в модели считаемого бесконечно коротким, когда эта сила бесконечна. Поэтому можно говорить не о «мгновенной», а об эффективной силе :

${\displaystyle F={\frac {\Delta p}{\Delta t}}={\frac {mv_{x}^{2}}{L}}}$ .

Если в сосуде не одна, а ${\displaystyle N}$ не взаимодействующих между собой частиц, то сила будет суммироваться по всем частицам. При этом, по-прежнему, модуль ${\displaystyle x}$ -проекции скорости отдельной частицы неизменен, но для разных частиц различен. Соответственно, появляется усреднение квадрата проекции скорости:

${\displaystyle F_{\Sigma }=F_{1}+F_{2}+\ldots +F_{N}={\frac {Nm{\overline {v_{x}^{2}}}}{L}}}$ .

Скорость частицы состоит из трёх компонент, и из теоремы Пифагора ${\displaystyle v^{2}=v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}$ . Это равенство можно усреднить по всем частицам:

${\displaystyle {\overline {v^{2}}}={\overline {v_{x}^{2}}}+{\overline {v_{y}^{2}}}+{\overline {v_{z}^{2}}}}$ ,

причём, ввиду эквивалентности направлений, три члена в правой части обязаны быть одинаковыми. В результате

${\displaystyle {\overline {v_{x}^{2}}}={\frac {1}{3}}\,{\overline {v^{2}}}}$ ,

после чего получается

${\displaystyle F_{\Sigma }={\frac {Nm{\overline {v^{2}}}}{3L}}}$ .

Если учесть, что давление есть сила на единицу площади, а ${\displaystyle S=L^{2}}$ , имеем

${\displaystyle P={\frac {F_{\Sigma }}{S}}={\frac {Nm{\overline {v^{2}}}}{3L^{3}}}={\frac {Nm{\overline {v^{2}}}}{3V}}}$ ,

где ${\displaystyle V}$ — объём рассмотренного кубического сосуда. Это и есть основное уравнение МКТ, поскольку ${\displaystyle N/V=n}$ .

Температура в уравнении МКТ

Кинетическая энергия движения ${\displaystyle N}$ молекул газа может быть записана как

${\displaystyle K_{\Sigma }=N{\frac {1}{2}}m{\overline {v^{2}}}=N{\overline {\frac {mv^{2}}{2}}}=N{\overline {K}}}$ ,

где через ${\displaystyle K}$ обозначена кинетическая энергия одной частицы. В этих обозначениях основное уравнение МКТ переписывается в виде

${\displaystyle PV={\frac {2}{3}}K_{\Sigma }}$ .

Согласно уравнению состояния идеального газа ,

${\displaystyle PV=Nk_{B}T}$ ,

где ${\displaystyle T}$ — температура . а ${\displaystyle k_{B}}$ — постоянная Больцмана . Из сравнения двух последних выражений видно, что

${\displaystyle {\overline {K}}={\frac {3}{2}}\,k_{B}T}$ ,

то есть что температура выступает мерой средней кинетической энергии частиц.

При потребности в формулах можно провести преобразования с использованием соотношений для количества вещества (числа молей ) ${\displaystyle \nu =N/N_{A}}$ ( ${\displaystyle N_{A}}$ — постоянная Авогадро ) и газовой постоянной ${\displaystyle R=N_{A}k_{B}}$ .

Средняя скорость частиц

Понятием «средняя скорость» охватывается несколько величин. Одна из средних скоростей, так называемая среднеквадратичная скорость, — это корень из среднего квадрата скорости:

${\displaystyle {\overline {v_{q}}}={\sqrt {\overline {v^{2}}}}}$ .

Она может быть выписана на основе уравнений выше, учитывая, что там фигурировала ${\displaystyle {\overline {v^{2}}}}$ , а именно:

${\displaystyle {\overline {v_{q}}}={\sqrt {\frac {3k_{B}T}{m}}}}$ .

Если учесть, что ${\displaystyle N_{A}m=M}$ , где ${\displaystyle M}$ — молярная масса газа, получим

${\displaystyle {\overline {v_{q}}}={\sqrt {\frac {3k_{B}TN_{A}}{M}}}}$ .

Другие средние скорости (например, средний модуль скорости) не могут быть определены таким образом, для их нахождения используется распределение Максвелла .

См. также

• Физическая кинетика
• Статистическая механика
• Статистическая физика
• Распределение Максвелла

Примечания

Литература

• // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб. , 1890—1907.
• Гиршфельд Дж., Кертисс Ч., Берд Р. Молекулярная теория газов и жидкостей. М., 1961
• Френкель Я. И. Кинетическая теория жидкостей. Л., 1975
• Кикоин А. К., Кикоин И. К. Молекулярная физика . М., 1996