Interested Article - Геостационарная орбита

Вид Земли с высоты около 30 тысяч км ( Аполлон-8 )

Геостациона́рная орби́та (ГСО) — круговая орбита , расположенная над экватором Земли (0° широты), находясь на которой, искусственный спутник обращается вокруг планеты с угловой скоростью , равной угловой скорости вращения Земли вокруг оси. В горизонтальной системе координат направление на спутник не изменяется ни по азимуту, ни по высоте над горизонтом — спутник «висит» в небе неподвижно. Поэтому спутниковая антенна , однажды направленная на такой спутник, всё время остаётся направленной на него. Геостационарная орбита является разновидностью геосинхронной орбиты и используется для размещения искусственных спутников (коммуникационных, телетрансляционных и т. п.).

Спутник должен обращаться в направлении вращения Земли, на высоте 35 786 км над уровнем моря (вычисление высоты ГСО). Именно такая высота обеспечивает спутнику период обращения, равный периоду вращения Земли относительно звёзд ( Звёздные сутки : 23 часа 56 минут 4,091 секунды).

Идея использования геостационарных спутников для целей связи высказывалась ещё словенским теоретиком космонавтики Германом Поточником в 1928 году .

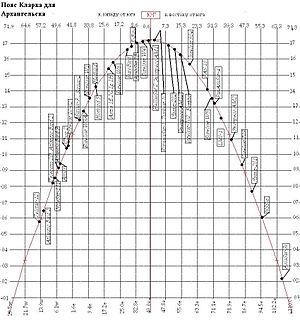
Преимущества геостационарной орбиты получили широкую известность после выхода в свет научно-популярной статьи Артура Кларка в журнале « » в 1945 году , поэтому на Западе геостационарная и геосинхронные орбиты иногда называются « орбитами Кларка », а « поясом Кларка » называют область космического пространства на расстоянии 36 000 км над уровнем моря в плоскости земного экватора, где параметры орбит близки к геостационарной. Первым спутником, успешно выведенным на ГСО, был , запущенный NASA в августе 1964 года .

Точка стояния

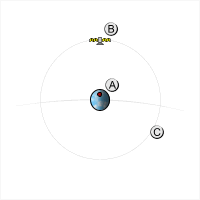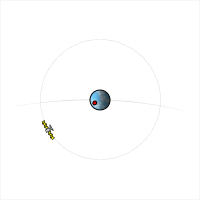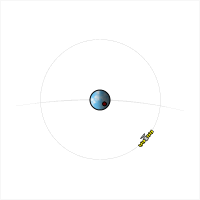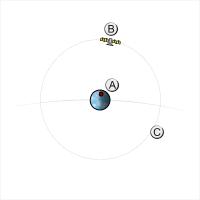
Спутник, находящийся на геостационарной орбите , неподвижен относительно поверхности Земли , поэтому его местоположение на орбите называется точкой стояния . В результате сориентированная на спутник и неподвижно закреплённая направленная антенна может сохранять постоянную связь с этим спутником длительное время.

Размещение спутников на орбите

Для Архангельска максимально возможная высота спутника над горизонтом — 17,2°
Наивысшая точка пояса Кларка всегда находится строго на юге (для северного полушария). В нижней части графика градусы — меридианы, над которыми находятся спутники.
По бокам — высоты спутников над горизонтом.
Сверху — направление на спутник. Для наглядности можно растянуть по горизонтали в 7,8 раза и отразить слева направо. Тогда он будет выглядеть так же, как на небе.

Геостационарная орбита может быть точно обеспечена только на окружности, расположенной прямо над экватором, с высотой, очень близкой к 35 786 км .

Если бы геостационарные спутники были видны на небе невооружённым глазом, то линия, на которой они были бы видны, совпадала бы с «поясом Кларка» для данной местности. Геостационарные спутники, благодаря имеющимся точкам стояния, удобно использовать для спутниковой связи: единожды сориентированная антенна всегда будет направлена на выбранный спутник (если он не сменит позицию).

Для перевода спутников с низковысотной орбиты на геостационарную используются переходные геостационарные (геопереходные) орбиты ( ГПО ) — эллиптические орбиты с перигеем на низкой высоте и апогеем на высоте, близкой к геостационарной орбите.

После завершения срока активного существования (САС) на остатках топлива спутник должен быть переведён на орбиту захоронения , расположенную на 200—300 км выше ГСО.

Существуют каталоги объектов на геостационарной орбите .

Вычисление параметров геостационарной орбиты

Радиус орбиты и высота орбиты

На геостационарной орбите спутник не приближается к Земле и не удаляется от неё, и кроме того, вращаясь вместе с Землёй, постоянно находится над какой-либо точкой на экваторе. Следовательно, действующие на спутник силы гравитации и центробежная сила должны уравновешивать друг друга. Для вычисления высоты геостационарной орбиты можно воспользоваться методами классической механики и, перейдя в систему отсчета спутника, исходить из следующего уравнения:

F_{u}=F_{\Gamma }

F_{{u}}=F_{{\Gamma }}

,

где $F_{u}$ $F_{{u}}$ — сила инерции, а в данном случае, центробежная сила; $F_{\Gamma }$ $F_{{\Gamma }}$ — гравитационная сила. Величину гравитационной силы, действующую на спутник, можно определить по закону всемирного тяготения Ньютона :

F_{\Gamma }=G\cdot {\frac {M_{3}\cdot m_{c}}{R^{2}}}

F_{{\Gamma }}=G\cdot {\frac {M_{3}\cdot m_{c}}{R^{2}}}

,

где $m_{c}$ $m_{c}$ — масса спутника, $M_{3}$ $M_{3}$ — масса Земли в килограммах , $G$ $G$ — гравитационная постоянная , а $R$ $R$ — расстояние в метрах от спутника до центра Земли или, в данном случае, радиус орбиты.

Величина центробежной силы равна:

F_{u}=m_{c}\cdot a

F_{{u}}=m_{c}\cdot a

,

где $a$ $a$ — центростремительное ускорение, возникающее при круговом движении по орбите.

Как можно видеть, масса спутника $m_{c}$ $m_{c}$ присутствует как множитель в выражениях для центробежной силы и для гравитационной силы, то есть высота орбиты не зависит от массы спутника, что справедливо для любых орбит и является следствием равенства гравитационной и инертной массы . Следовательно, геостационарная орбита определяется лишь высотой, при которой центробежная сила будет равна по модулю и противоположна по направлению гравитационной силе, создаваемой притяжением Земли на данной высоте.

Центростремительное ускорение равно:

a=\omega ^{2}\cdot R

a=\omega ^{2}\cdot R

,

где $\omega$ $\omega$ — угловая скорость вращения спутника, в радианах в секунду.

Сделаем одно важное уточнение. В действительности, центростремительное ускорение имеет физический смысл только в инерциальной системе отсчета, в то время как центробежная сила является так называемой мнимой силой и имеет место исключительно в системах отсчета (координат), которые связаны с вращающимися телами. Центростремительная сила (в данном случае — сила гравитации) вызывает центростремительное ускорение. По модулю центростремительное ускорение в инерциальной системе отсчета равно центробежному в системе отсчета, связанной в нашем случае со спутником. Поэтому далее, с учётом сделанного замечания, мы можем употреблять термин «центростремительное ускорение» вместе с термином «центробежная сила».

Уравнивая выражения для гравитационной и центробежной сил с подстановкой центростремительного ускорения, получаем:

m_{c}\cdot \omega ^{2}\cdot R=G\cdot {\frac {M_{3}\cdot m_{c}}{R^{2}}}

m_{c}\cdot \omega ^{2}\cdot R=G\cdot {\frac {M_{3}\cdot m_{c}}{R^{2}}}

.

Сокращая $m_{c}$ $m_{c}$ , переводя $R^{2}$ $R^2$ влево, а $\omega ^{2}$ $\omega ^{2}$ вправо, получаем:

R^{3}=G\cdot {\frac {M_{3}}{\omega ^{2}}}

R^{3}=G\cdot {\frac {M_{3}}{\omega ^{2}}}

или

R={\sqrt[{3}]{\frac {G\cdot M_{3}}{\omega ^{2}}}}

R={\sqrt[ {3}]{{\frac {G\cdot M_{3}}{\omega ^{2}}}}}

.

Можно записать это выражение иначе, заменив $G\cdot M_{3}$ $G\cdot M_{3}$ на $\mu$ $\mu$ — геоцентрическую гравитационную постоянную:

R={\sqrt[{3}]{\frac {\mu }{\omega ^{2}}}}

R={\sqrt[ {3}]{{\frac {\mu }{\omega ^{2}}}}}

Угловая скорость $\omega$ $\omega$ вычисляется делением угла, пройденного за один оборот ( $360^{\circ }=2\cdot \pi$ $360^{\circ }=2\cdot \pi$ радиан) на период обращения (время, за которое совершается один полный оборот по орбите: один сидерический день , или 86 164 секунды ). Получаем:

\omega ={\frac {2\cdot \pi }{86164}}=7,29\cdot 10^{-5}

\omega ={\frac {2\cdot \pi }{86164}}=7,29\cdot 10^{{-5}}

рад/с

Полученный радиус орбиты составляет 42 164 км . Вычитая экваториальный радиус Земли, 6378 км, получаем высоту 35 786 км .

Можно сделать вычисления и иначе. Высота геостационарной орбиты — это такое удаление от центра Земли, где угловая скорость спутника, совпадающая с угловой скоростью вращения Земли, порождает орбитальную (линейную) скорость, равную первой космической скорости (для обеспечения круговой орбиты) на данной высоте.

Линейная скорость спутника, движущегося с угловой скоростью $\omega$ $\omega$ на расстоянии $R$ $R$ от центра вращения равна

v_{l}=\omega \cdot R

v_{l}=\omega \cdot R

Первая космическая скорость на расстоянии $R$ $R$ от объекта массой $M$ $M$ равна

v_{k}={\sqrt {G{\frac {M}{R}}}};

v_{k}={\sqrt {G{\frac {M}{R}}}};

Приравняв правые части уравнений друг к другу, приходим к полученному ранее выражению радиуса ГСО:

R={\sqrt[{3}]{G{\frac {M}{\omega ^{2}}}}}

R={\sqrt[ {3}]{G{\frac {M}{\omega ^{2}}}}}

Орбитальная скорость

Скорость движения по геостационарной орбите вычисляется умножением угловой скорости на радиус орбиты:

v=\omega \cdot R=3{,}07

v=\omega \cdot R=3{,}07

км/с

Это примерно в 2,5 раза меньше, чем первая космическая скорость , равная 8 км/с на околоземной орбите (с радиусом 6400 км). Так как квадрат скорости для круговой орбиты обратно пропорционален её радиусу,

v={\sqrt {G{\frac {M}{R}}}};

v={\sqrt {G{\frac {M}{R}}}};

то уменьшение скорости по отношению к первой космической достигается увеличением радиуса орбиты более чем в 6 раз.

R\approx \,\!{6400\cdot \left({\frac {8}{3{,}07}}\right)^{2}}\approx \,\!43000

R\approx \,\!{6400\cdot \left({\frac {8}{3{,}07}}\right)^{2}}\approx \,\!43000

Длина орбиты

Длина геостационарной орбиты: ${2\cdot \pi \cdot R}$ ${2\cdot \pi \cdot R}$ . При радиусе орбиты 42 164 км получаем длину орбиты 264 924 км .

Длина орбиты крайне важна для вычисления « точек стояния » спутников.

Удержание спутника в орбитальной позиции на геостационарной орбите

Спутник, обращающийся на геостационарной орбите, находится под воздействием ряда сил (возмущений), изменяющих параметры этой орбиты. В частности, к таким возмущениям относятся гравитационные лунно-солнечные возмущения, влияние неоднородности гравитационного поля Земли, эллиптичность экватора и т. д. Деградация орбиты выражается в двух основных явлениях:

1) Спутник смещается вдоль орбиты от своей первоначальной орбитальной позиции в сторону одной из четырёх точек стабильного равновесия, т. н. «потенциальных ям геостационарной орбиты» (их долготы 75,3°E, 104,7°W, 165,3°E, и 14,7°W) над экватором Земли;

2) Наклонение орбиты к экватору увеличивается (от первоначального 0) со скоростью порядка 0,85 градусов в год и достигает максимального значения 15 градусов за 26,5 лет.

Для компенсации этих возмущений и удержания спутника в назначенной точке стояния спутник оснащается двигательной установкой ( химической или электроракетной ). Периодическими включениями двигателей малой тяги (коррекция «север — юг» для компенсации роста наклонения орбиты и «запад — восток» для компенсации дрейфа вдоль орбиты) спутник удерживается в назначенной точке стояния. Такие включения производятся по нескольку раз в 10 — 15 суток. Существенно, что для коррекции «север — юг» требуется значительно большее приращение характеристической скорости (около 45 — 50 м/с в год), чем для долготной коррекции (около 2 м/с в год). Для обеспечения коррекции орбиты спутника на протяжении всего срока его эксплуатации (12 — 15 лет для современных телевизионных спутников) требуется значительный запас топлива на борту (сотни килограммов в случае применения химического двигателя). Химический ракетный двигатель спутника имеет вытеснительную подачу топлива (газ наддува — гелий), работает на долгохранимых высококипящих компонентах (обычно несимметричный диметилгидразин и диазотный тетраоксид ). На ряде спутников устанавливаются плазменные двигатели. Их тяга существенно меньше по отношению к химическим, однако большая эффективность позволяет (за счёт продолжительной работы, измеряемой десятками минут для единичного манёвра) радикально снизить требуемую массу топлива на борту. Выбор типа двигательной установки определяется конкретными техническими особенностями аппарата.

Эта же двигательная установка используется при необходимости для манёвра перевода спутника в другую орбитальную позицию. В некоторых случаях (как правило, в конце срока эксплуатации спутника) для сокращения расхода топлива коррекция орбиты «север — юг» прекращается, а остаток топлива используется только для коррекции «запад — восток».

Запас топлива является основным лимитирующим фактором САС спутника на геостационарной орбите (кроме отказов компонентов самого спутника). Однако некоторые страны проводят эксперименты с дозаправкой действующих спутников прямо на ГСО для продления САС .

Недостатки геостационарной орбиты

Задержка сигнала

Связь через геостационарные спутники характеризуется большими задержками в распространении сигнала. При высоте орбиты 35 786 км и скорости света около 300 000 км/с ход луча «Земля — спутник» требует около 0,12 с, ход луча «Земля (передатчик) → спутник → Земля (приемник)» ≈0,24 с (то есть полная задержка (измеряемая утилитой Ping ) при использовании спутниковой связи для приема и передачи данных составит почти полсекунды). С учётом задержки сигнала в аппаратуре ИСЗ, в аппаратуре и в кабельных системах передач наземных служб общая задержка сигнала на маршруте «источник сигнала → спутник → приёмник» может достигать 2—4 секунд . Такая задержка затрудняет применение спутников на ГСО в телефонии и делает невозможной применение спутниковой связи с использованием ГСО в различных сервисах реального времени (например в онлайн-играх ) .

Невидимость ГСО с высоких широт

Так как геостационарная орбита не видна с высоких широт (приблизительно от 81° до полюсов), а на широтах выше 75° наблюдается очень низко над горизонтом (в реальных условиях спутники просто скрываются выступающими объектами и рельефом местности) и виден лишь небольшой участок орбиты ( см. таблицу ), то в высокоширотных районах Крайнего Севера (Арктики) и Антарктиды невозможна связь и телетрансляция с использованием ГСО .

Таблица наблюдаемого сектора геостационарной орбиты в зависимости от широты места
Все данные приведены в градусах и их долях.

Широта местности	Видимый сектор орбиты
Широта местности	Теоретический сектор	Реальный (с уч. рельефа) сектор
90	--	--
82	--	--
81	29,7	--
80	58,9	--
79	75,2	--
78	86,7	26,2
75	108,5	77
60	144,8	132,2
50	152,8	143,3
40	157,2	149,3
20	161,5	155,1
0	162,6	156,6

Из таблицы видно, например, что если на широте Санкт-Петербурга (~60°) видимый сектор орбиты (и, соответственно, количество принимаемых спутников) равен 84 % от максимально возможного (на экваторе ), то на широте полуострова Таймыр (~75°) видимый сектор составляет 49 %, а на широте Шпицбергена и мыса Челюскина (~78°) — лишь 16 % от наблюдаемого на экваторе. В этот сектор орбиты в районе Таймыра попадает 1 — 2 спутника (не всегда необходимого оператора).

Солнечная интерференция

Одним из самых неприятных недостатков геостационарной орбиты является уменьшение и полное отсутствие сигнала в ситуации, когда солнце и спутник находятся на одной линии с приёмной антенной (положение «солнце за спутником»). Данное явление присуще и другим орбитам, но именно на геостационарной, когда спутник «неподвижен» на небе, проявляется особенно ярко. В средних широтах северного полушария солнечная интерференция проявляется в периоды с 22 февраля по 11 марта и с 3 по 21 октября, с максимальной длительностью до десяти минут . В такие моменты в ясную погоду солнечные лучи, сфокусированные светлым покрытием антенны могут даже повредить (расплавить или перегреть) приёмо-передающую аппаратуру спутниковой антенны .

Международно-правовой статус ГСО

Использование геостационарной орбиты ставит целый ряд не только технических, но и международно-правовых проблем. Значительный вклад в их разрешение вносит ООН, а также её комитеты и иные специализированные учреждения.

Некоторые экваториальные страны в разное время предъявляли претензии (например, Декларация об установлении суверенитета на участке ГСО, подписанная в Боготе Бразилией , Колумбией , Конго , Эквадором , Индонезией , Кенией , Угандой и Заиром 3 декабря 1976 г. ) на распространение их суверенитета на находящуюся над их территориями часть космического пространства, в которой проходят орбиты геостационарных спутников. Было, в частности, заявлено, что геостационарная орбита является физическим фактором, связанным с существованием нашей планеты и полностью зависящим от гравитационного поля Земли, а потому соответствующие части космоса (сегменты геостационарной орбиты) как бы являются продолжением территорий, над которыми они находятся. Соответствующее положение закреплено в Конституции Колумбии .

Эти притязания экваториальных государств были отвергнуты, как противоречащие принципу неприсвоения космического пространства. В Комитете ООН по космосу такие заявления подверглись критике. Во-первых, нельзя претендовать на присвоение какой-либо территории или пространства, находящегося на таком значительном удалении от территории соответствующего государства. Во-вторых, космическое пространство не подлежит национальному присвоению. В-третьих, технически неправомочно говорить о какой-либо физической взаимосвязи между государственной территорией и столь отдаленным районом космоса. Наконец, в каждом отдельном случае феномен геостационарного спутника связан с конкретным космическим объектом. Если нет спутника, то нет и геостационарной орбиты.

См. также

Примечания

Noordung, Hermann; et al. The Problem With Space Travel. — DIANE Publishing, 1995. — С. 72. — ISBN 978-0788118494 .
(англ.) (pdf). Arthur C. Clark (октябрь 1945). Дата обращения: 25 февраля 2010. 23 августа 2011 года.
Требование неподвижности спутников относительно Земли на своих орбитальных позициях на геостационарной орбите, а также большое количество спутников на этой орбите в разных её точках, приводят к интересному эффекту при наблюдении и фотографировании звёзд с помощью телескопа с использованием гидирования — удержания ориентации телескопа на заданной точке звёздного неба для компенсации суточного вращения Земли (задача, обратная геостационарной радиосвязи). Если наблюдать в такой телескоп звёздное небо вблизи небесного экватора , где проходит геостационарная орбита, то при определённых условиях можно видеть, как спутники друг за другом проходят на фоне неподвижных звёзд в пределах узкого коридора, как автомобили по оживлённой автотрассе. Особенно хорошо это заметно на фотографиях звёзд с длительными экспозициями, смотри, например: Babak A. Tafreshi. (англ.) . The World At Night (TWAN). Дата обращения: 25 февраля 2010. 23 августа 2011 года. Источник: Бабак Тафреши (Ночной мир). (рус.) Астронет . Дата обращения: 25 февраля 2010. 22 ноября 2011 года.
(неопр.) . Дата обращения: 5 июня 2018. 19 октября 2018 года.
для орбит спутников, масса которых пренебрежимо мала по сравнению с массой притягивающего его астрономического объекта
(неопр.) . www.dailytechinfo.org (22 января 2013). Дата обращения: 14 июня 2020. Архивировано из 14 июня 2020 года.
(рус.) . www.livejournal.com (22 августа 2016). Дата обращения: 14 июня 2020. 26 августа 2016 года.
(неопр.) . Дата обращения: 13 февраля 2009. Архивировано из 25 августа 2016 года.
(неопр.) . Дата обращения: 29 февраля 2012. 6 марта 2016 года.
(неопр.) . Дата обращения: 29 февраля 2012. 7 ноября 2012 года.
взято превышение спутником горизонта в 3°
(неопр.) Дата обращения: 9 марта 2012. 5 марта 2016 года.
(неопр.) . Дата обращения: 9 марта 2012. Архивировано из 17 августа 2013 года.
B.IV.1. Declaration of the First Meeting of Equatorial Countries ("Bogota Declaration") of December 3, 1976 // / Karl-Heinz Böckstiegel, Marietta Benkö, Stephan Hobe. — Eleven International Publishing, 2005. — ISBN 9780792300915 .
(неопр.) . Дата обращения: 1 августа 2014. 13 ноября 2013 года.