Interested Article - Ускорение свободного падения

isla
  • 2021-11-22
  • 2

Ускорение свободного падения на поверхности некоторых небесных тел, м/с² и g
Земля 9,81 м/с² 1,00 g Солнце 273,1 м/с² 27,85 g
Луна 1,62 м/с² 0,165 g Меркурий 3,70 м/с² 0,378 g
Венера 8,88 м/с² 0,906 g Марс 3,86 м/с² 0,394 g
Юпитер 24,79 м/с² 2,528 g Сатурн 10,44 м/с² 1,065 g
Уран 8,86 м/с² 0,903 g Нептун 11,09 м/с² 1,131 g
Эрида 0,82 ± 0,02 м/с² 0,084 ± 0,002 g Плутон 0,617 м/с² 0,063 g

Ускоре́ние свобо́дного паде́ния ( ускорение силы тяжести ) — ускорение , придаваемое телу силой тяжести (или, иными словами, ускорение тела при свободном падении ), при исключении из рассмотрения других сил.

В соответствии с уравнением движения тел в неинерциальных системах отсчёта ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы .

Ускорение свободного падения на поверхности Земли g (обычно произносится как «же» ) варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах . Стандартное («нормальное») значение, принятое при построении систем единиц , составляет 9,80665 м/с² . Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле: оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря . В приблизительных расчётах его обычно округляют до 9,81, 9,8 или даже до 10 м/с².

Физическая сущность

Две компоненты ускорения свободного падения на Земле g : гравитационная (в приближении сферически симметричной зависимости плотности от расстояния от центра Земли) равна GM/r 2 и центробежная, равная ω 2 a , где a — расстояние до земной оси, ω — угловая скорость вращения Земли.

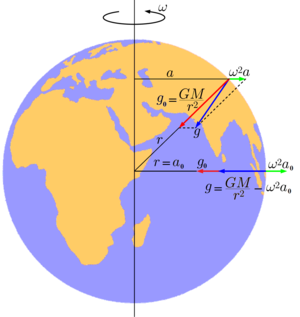
Для определённости будем считать, что речь идёт о свободном падении на Земле. Эту величину можно представить как векторную сумму двух слагаемых: гравитационного ускорения , вызванного земным притяжением, и центробежного ускорения , связанного с вращением Земли .

Центробежное ускорение

Центробежное ускорение является следствием вращения Земли вокруг своей оси. Именно центробежное ускорение, вызванное вращением Земли вокруг своей оси, вносит наибольший вклад в неинерциальность системы отсчёта , связанную с Землёй. В точке, находящейся на расстоянии a от оси вращения, оно равно ω 2 a , где ω — угловая скорость вращения Земли, определяемая как ω = 2π/ T , а Т — время одного оборота вокруг своей оси, для Земли равное 86164 секундам ( звёздные сутки ). Центробежное ускорение направлено по нормали к оси вращения Земли. На экваторе оно составляет 3,39636 см/с², причём на других широтах направление вектора его не совпадает с направлением вектора гравитационного ускорения, направленного к центру Земли.

Гравитационное ускорение

Гравитационное ускорение на различной высоте h над уровнем моря
h , км g , м/с² h , км g , м/с²
0 9,8066 20 9,7452
1 9,8036 50 9,6542
2 9,8005 80 9,5644
3 9,7974 100 9,505
4 9,7943 120 9,447
5 9,7912 500 8,45
6 9,7882 1000 7,36
8 9,7820 10 000 1,50
10 9,7759 50 000 0,125
15 9,7605 400 000 0,0025

В соответствии с законом всемирного тяготения , величина гравитационного ускорения на поверхности Земли или космического тела связана с его массой M следующим соотношением:

g = G M r 2 {\displaystyle g=G{\frac {M}{r^{2}}}} ,

где G — гравитационная постоянная (6,67430[15]·10 −11 м 3 · с −2 · кг −1 ) , а r — радиус планеты. Это соотношение справедливо в предположении, что плотность вещества планеты сферически симметрична. Приведённое соотношение позволяет определить массу любого космического тела, включая Землю, зная её радиус и гравитационное ускорение на её поверхности, либо, наоборот, по известной массе и радиусу определить ускорение свободного падения на поверхности.

Исторически масса Земли была впервые определена Генри Кавендишем , который провёл первые измерения гравитационной постоянной.

Гравитационное ускорение на высоте h над поверхностью Земли (или иного космического тела) можно вычислить по формуле:

g ( h ) = G M ( r + h ) 2 {\displaystyle g(h)={\frac {GM}{(r+h)^{2}}}} ,
где M — масса планеты.

Ускорение свободного падения на Земле

Ускорение свободного падения у поверхности Земли зависит от широты. Приблизительно оно может быть вычислено (в м/с²) по эмпирической формуле :

g = 9,780 318 ( 1 + 0,005 302 sin 2 ⁡ φ − 0,000 006 sin 2 ⁡ 2 φ ) − 0,000 003086 h , {\displaystyle g=9{,}780318(1+0{,}005302\sin ^{2}\varphi -0{,}000006\sin ^{2}2\varphi)-0{,}000003086h,}
где φ {\displaystyle \varphi } — широта рассматриваемого места,
h {\displaystyle h} — высота над уровнем моря в метрах .

Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. При более точных расчётах необходимо использовать одну из , дополнив её поправками, связанными с вращением Земли, приливными воздействиями . На ускорение свободного падения влияют и другие факторы, например, атмосферное давление , которое меняется в течение суток: от атмосферного давления зависит плотность воздуха в большом объёме, а следовательно и результирующая сила тяжести, изменение которой могут зафиксировать высокочувствительные гравиметры .

Пространственные изменения гравитационного поля Земли ( гравитационные аномалии ) связаны с неоднородности плотности в её недрах, что может быть использовано для поиска залежей полезных ископаемых методами гравиразведки .

Почти везде ускорение свободного падения на экваторе ниже, чем на полюсах, за счёт центробежных сил, возникающих при вращении планеты, а также потому, что радиус r на полюсах меньше, чем на экваторе из-за сплюснутой формы планеты. Однако места экстремально низкого и высокого значения g несколько отличаются от теоретических показателей по этой модели. Так, самое низкое значение g (9,7639 м/с²) зафиксировано на горе Уаскаран в Перу в 1000 км южнее экватора, а самое большое (9,8337 м/с²) — в 100 км от Северного полюса .

Измерение

Основная статья: Гравиметрия (геодезия)

Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра . Различают две разновидности гравиметров: абсолютные и относительные. Абсолютные гравиметры измеряют ускорение свободного падения непосредственно. Относительные гравиметры, некоторые модели которых действуют по принципу пружинных весов, определяют приращение ускорения свободного падения относительно значения в некотором исходном пункте.

Ускорение свободного падения на поверхности Земли или другой планеты может быть также вычислено на основе данных о вращении планеты и её гравитационном поле. Последнее может быть определено посредством наблюдения за орбитами спутников и движения других небесных тел вблизи рассматриваемой планеты.

См. также

Примечания

  1. У планет газовых гигантов и звёзд «поверхность» понимается как область меньших высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×10 5 Па ). Также у звёзд поверхностью иногда считают поверхность фотосферы .
  2. Аналог уравнения второго закона Ньютона , выполняющийся для неинерциальных систем отсчёта.
  3. (неопр.) . Архивировано из 20101219 года.
  4. (англ.) . Международное бюро мер и весов . Дата обращения: 9 апреля 2013. 8 июля 2018 года.
  5. Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Изд-во стандартов, 1990. — С. 237.
  6. (неопр.) . physics.nist.gov. Дата обращения: 7 марта 2020. 23 сентября 2020 года.
  7. Грушинский Н. П. // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров . — М. : Советская энциклопедия , 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 521. — 707 с. — 100 000 экз.
  8. // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров . — М. : Большая российская энциклопедия , 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 245—246. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8 .
  9. (англ.) . Дата обращения: 10 ноября 2021. Архивировано из 24 августа 2013 года.
  10. // Геология и геофизика. — 2015. — Т. 56 , вып. 5 . — doi : . 2 июня 2018 года.
  11. (неопр.) Дата обращения: 21 июля 2016. 16 сентября 2016 года.

Литература

  • Енохович А. С. Краткий справочник по физике. — М. : Высшая школа, 1976. — 288 с.

isla
  • 2021-11-22
  • 2

Same as Ускорение свободного падения

The title for the last searches