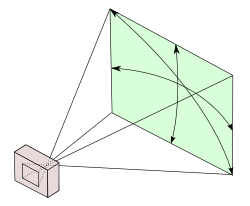
В математике (в частности, в геометрии и тригонометрии ) и во всех естественных науках (например, в астрономии и геофизике ) угловое расстояние — это мера видимого расстояния между двумя точками или объектами, выраженная в угловых единицах дуги, при условии, что наблюдатель находится в вершине угла, концами которого являются две рассматриваемые точки. Угловой диаметр является частным случаем углового размера .

Угловое расстояние является фундаментальной величиной в астрономии , определяющей положение любого объекта на небесной сфере по его небесным координатам : либо в угловых единицах, либо во времени. Азимут , высота , склонение или прямое восхождение объекта на небе, среди прочего, являются небесными координатами. Любое из них — это угловое расстояние до точки или плоскости отсчета: горизонта , небесного экватора , меридиана и т. д.

Использование

Термин угловое расстояние технически синонимичен самому углу, но предназначен для обозначения линейного расстояния (часто огромного и неизвестного) между этими объектами (например, звездами , наблюдаемыми с Земли ).

Для визуальных наблюдений без претензий на точность можно вычислить угловое расстояние, конечно, с приближениями порядка степени, и, конечно, очень грубо.

Отдельные вариации — длина руки, толщина пальцев и т. д. — меняют значения в первых приближениях, но не так важны для определения местоположения звезды или планеты , видимой невооруженным глазом или для связи созвездия с соседями.

Измерение

Поскольку угловое расстояние концептуально совпадает с углом, оно измеряется в тех же единицах , например, градусах или радианах и с использованием таких приборов, как гониометры или оптические приборы, специально предназначенные для поворота в четко определенных направлениях и записи соответствующих углов (такие как телескопы ).

Вычисление

Чтобы рассчитать угловое расстояние θ в угловых секундах для двойной звёздные системы , экзопланеты , объекта Солнечной системы и других астрономических объектов , используется размер большой полуоси , выраженной в астрономических единицах (а.е.), деленное на расстояние D, выраженное в парсеках , согласно формуле для малых углов — ${\displaystyle \tan({\frac {a}{D}})}$ :

${\displaystyle \theta \approx {\dfrac {a}{D}}}$

Учитывая два угловых положения, каждое из которых определяется прямым восхождением (RA), ${\displaystyle \alpha \in [0,2\pi ]}$ и склонением (dec), ${\displaystyle \delta \in [-\pi /2,\pi /2]}$ угловое расстояние между двумя точками можно рассчитать, используя следующую формулу:

${\displaystyle \theta =\cos ^{-1}\left[\sin(\delta _{1})\sin(\delta _{2})+\cos(\delta _{1})\cos(\delta _{2})\cos(\alpha _{1}-\alpha _{2})\right]}$

См. также

• Тысячная
• Град, минута, секунда
• Часовой угол
• Центральный угол
• Угловой размер
• Ортодромия

Литература

• Климишин И. А. (рус.) . — Рипол Классик, 1980. — С. 99. — 561 с.
• Weisstein, Eric W. (англ.) . — MathWorld .