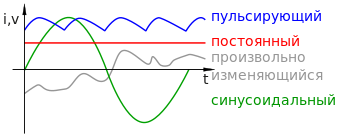
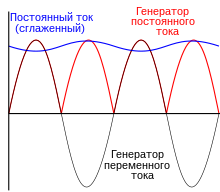
Переме́нный ток — электрический ток , который с течением времени изменяется по величине , обычно и по направлению в электрической цепи .

Хотя переменный ток часто переводят на английский как alternating current , эти термины не эквивалентны. Термин alternating current (AC) в узком смысле означает синусоидальный ток, в широком смысле — периодический знакопеременный ток (то есть периодический двунаправленный ток). Условное обозначение на электроприборах: ${\displaystyle \thicksim }$ или ${\displaystyle \thickapprox }$ (знак синусоиды ), или латинскими буквами ${\displaystyle AC}$ .

Общее понятие о переменном токе

Так как переменный ток в общем случае меняется в электрической цепи не только по величине , но и по направлению, то одно из направлений переменного тока в цепи условно считают положительным, а другое отрицательным. В соответствии с этим и величину мгновенного значения переменного тока в первом случае считают положительной, а во втором случае — отрицательной.

Сила переменного тока — величина скалярная , знак её определяется тем, в каком направлении ток протекает в цепи в рассматриваемый момент времени — в положительном или отрицательном.

Величина переменного тока, соответствующая данному моменту времени, называется мгновенным значением переменного тока .

Максимальное мгновенное значение переменного тока, которого он достигает в процессе своего изменения, называется амплитудой тока ${\displaystyle I_{m}}$ .

График зависимости силы переменного тока от времени называется развёрнутой диаграммой переменного тока.

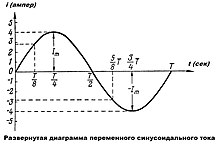
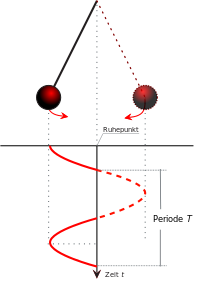
На рисунке приведена развёрнутая диаграмма переменного тока , изменяющегося с течением времени по величине и направлению. На горизонтальной оси — оси времени — в определённом масштабе отложены отрезки времени, а по вертикальной оси — сила тока, причём в направлении вверх выбрано положительное направление, а вниз — отрицательное.

В начальный момент времени ${\displaystyle t=0}$ сила тока равна нулю ${\displaystyle (i=0)}$ . Затем она с течением времени растёт в положительном направлении, в момент времени ${\displaystyle t={\frac {T}{4}}}$ достигает максимального значения , после чего убывает и в момент времени ${\displaystyle t={\frac {T}{2}}}$ становится равной нулю. Затем, пройдя через нулевое значение, ток меняет своё направление на противоположное, то есть сила тока становится отрицательной, затем она растёт по абсолютной величине (стремясь вниз), достигает максимума (по абсолютной величине) при ${\displaystyle t={\frac {3}{4}}T}$ , а после этого убывает (по абсолютной величине), стремясь к нулю, и при ${\displaystyle t=T}$ становится равной нулю.

Периодический переменный ток

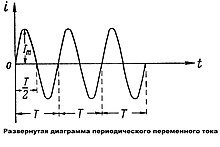
Периодическим переменным током называется такой электрический ток , который через равные промежутки времени повторяет полный цикл своих изменений, возвращаясь к своей исходной величине.

На представленной диаграмме через равные промежутки времени ${\displaystyle T}$ график тока воспроизводится полностью без каких-либо изменений.

Время ${\displaystyle T}$ , в течение которого переменный периодический ток совершает полный цикл своих изменений, возвращаясь к своей исходной величине, называется периодом переменного тока .

Величина, обратная периоду, называется частотой переменного тока:

${\displaystyle f={\frac {1}{T}}}$ , где:

${\displaystyle f}$ — частота переменного тока;

${\displaystyle T}$ — период переменного тока.

Если выразить время ${\displaystyle T}$ в секундах (s), то будем иметь:

${\displaystyle f={\frac {1}{T}}\left[{\frac {1}{\operatorname {s} }}\right]}$ , то есть размерность частоты переменного тока равна T ⁻¹ , а в СИ выражается в с ⁻¹ .

Частота переменного тока численно равна числу периодов по отношению к промежутку времени.

За единицу измерения частоты переменного тока принят 1 герц (Гц) — в честь Генриха Герца . Через основные единицы СИ герц выражается следующим образом: 1 Гц = 1 с ⁻¹ . Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ .

Частота переменного тока равна одному герцу, если период тока равен одной секунде (один полный цикл за одну секунду).

Стандарты частоты

В большинстве стран в электротехнике применяются частоты 50 или 60 Гц (вторая из них принята в США и Канаде ). В некоторых странах — например, в Японии — используются оба стандарта (см. « Промышленная частота переменного тока »).

Частота 16 ⅔ Гц до сих пор используется в некоторых европейских железнодорожных сетях ( Австрия , Германия , Норвегия , Швеция и Швейцария ), частота 25 Гц — на старых железнодорожных линиях США (см. статью ).

В авиации и военной технике, чтобы снизить массу устройств или повысить частоту вращения электродвигателей переменного тока, применяется частота 400 Гц.

Число оборотов ротора ${\displaystyle n\ [\operatorname {s} ^{-1}]}$ синхронного электродвигателя определяется по формуле:

${\displaystyle n={\tfrac {f}{p}}}$ , где

${\displaystyle f\ [\operatorname {s} ^{-1}]}$ — частота переменного тока;

${\displaystyle p}$ — число пар полюсов.

Так как минимальное число пар полюсов равно единице, то синхронный электродвигатель, работающий на переменном токе частотой 50 герц, разовьёт 3 000 оборотов в минуту, а электродвигатель, работающий на переменном токе частотой 400 герц, — 24 000 об/мин . Частота вращения ротора асинхронного электродвигателя меньше, чем частота питающего его тока и зависит от нагрузки. Скольжение — разность между частотой вращения вращающегося магнитного поля и частотой вращения ротора.

В технике передачи информации (в частности, в радиотехнике ) применяются частоты более высокие — порядка миллионов и миллиардов герц.

Переменный синусоидальный ток

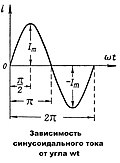
Синусоидальным током называется периодический переменный ток, который с течением времени изменяется по гармоническому закону .

Синусоидальный ток считается элементарным, то есть его невозможно разложить на другие более простые переменные токи .

Переменный синусоидальный ток выражается формулой:

${\displaystyle i=I_{m}\sin \omega t}$ , где

${\displaystyle I_{m}}$ — амплитуда синусоидального тока;

${\displaystyle \omega t}$ — некоторый угол , называемый фазой синусоидального тока .

Фаза синусоидального тока ${\displaystyle \omega t}$ изменяется пропорционально времени ${\displaystyle t}$ .

Множитель ${\displaystyle \omega }$ , входящий в выражение фазы ${\displaystyle \omega t,}$ — это угловая (круговая) частота переменного тока , которая является постоянной.

Угловая частота ${\displaystyle \omega }$ синусоидального тока зависит от частоты ${\displaystyle f}$ этого тока и определяется формулой:

${\displaystyle \omega =2\pi f={\frac {2\pi }{T}}}$ , где

${\displaystyle \omega }$ — угловая частота синусоидального тока;

${\displaystyle f}$ — частота синусоидального тока;

${\displaystyle T}$ — период синусоидального тока;

${\displaystyle 2\pi }$ — полный угол , выраженный в радианах .

Исходя из формулы ${\displaystyle \omega =2\pi f={\frac {2\pi }{T}}}$ , можно определить размерность угловой (круговой) частоты:

${\displaystyle \dim \omega =\dim {2\pi \over T}=\operatorname {T} ^{-1}}$ , где

${\displaystyle \operatorname {T} ^{-1}}$ — размерность времени в минус первой степени,

${\displaystyle 2\pi }$ — угол в радианах, являющийся безразмерной величиной.

Фаза ${\displaystyle \omega t}$ синусоидального тока измеряется радианами .

1 радиан = 57,29° = 57°17′, угол 90° = ${\displaystyle \pi \over 2}$ радиан, угол 180° = ${\displaystyle \pi }$ радиан, угол 270° = ${\displaystyle 3\pi \over 2}$ радиан, угол 360° = ${\displaystyle 2\pi }$ радиан,
где ${\displaystyle \pi =3{,}14}$ радиан; ${\displaystyle \pi }$ — число «пи» , ° — угловой градус и ′ — угловая минута .

---

Формула ${\displaystyle i=I_{m}\sin \omega t}$ описывает случай, когда наблюдение за изменением переменного синусоидального тока начинается с момента времени ${\displaystyle t=0}$ . Если начальный момент времени не равен нулю, тогда формула для определения мгновенного значения переменного синусоидального тока принимает следующий вид:

${\displaystyle i=I_{m}\sin(\omega t+\psi)}$ , где

${\displaystyle (\omega t+\psi)}$ — фаза переменного синусоидального тока;

${\displaystyle \psi }$ — угол , называемый начальной фазой переменного синусоидального тока .

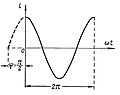
Если в формуле ${\displaystyle i=I_{m}\sin(\omega t+\psi)}$ принять ${\displaystyle t=0}$ , то будем иметь

${\displaystyle \omega t=0}$ , ${\displaystyle \omega t+\psi =\psi }$ и ${\displaystyle i_{t=0}=I_{m}\sin \psi }$ .

Начальная фаза — это фаза синусоидального тока в момент времени ${\displaystyle t=0}$ .

Начальная фаза переменного синусоидального тока может быть положительной ${\displaystyle (\psi >0)}$ или отрицательной ${\displaystyle (\psi <0)}$ величиной. При ${\displaystyle \psi >0}$ мгновенное значение синусоидального тока в момент времени ${\displaystyle t=0}$ положительно, при ${\displaystyle \psi <0}$ — отрицательно.

Если начальная фаза ${\displaystyle \psi ={\frac {\pi }{2}}}$ , то ток определяется по формуле ${\displaystyle i=I_{m}\sin(\omega t+{\frac {\pi }{2}})}$ . Мгновенное значение его в момент времени ${\displaystyle t=0}$ равно

${\displaystyle i_{t=0}=I_{m}\sin {\frac {\pi }{2}}=I_{m}}$ , то есть равно положительной амплитуде тока.

Если начальная фаза ${\displaystyle \psi =-{\frac {\pi }{2}}}$ , то ток определяется по формуле ${\displaystyle i=I_{m}\sin(\omega t-{\frac {\pi }{2}})}$ . Мгновенное значение его в момент времени ${\displaystyle t=0}$ равно

${\displaystyle i_{t=0}=I_{m}\sin(-{\frac {\pi }{2}})=-I_{m}}$ , то есть равно отрицательной амплитуде тока.

Многофазный переменный ток

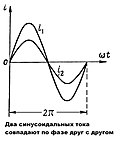
Два переменных синусоидальных тока совпадают по фазе , если они имеют одинаковые фазы и, следовательно, одновременно достигают своих нулевых и максимальных значений одинакового знака.

На левой иллюстрации представлены развёрнутые диаграммы токов ${\displaystyle i_{1}}$ и ${\displaystyle i_{2}}$ . Токи ${\displaystyle i_{1}=I_{1m}\sin \omega t}$ и ${\displaystyle i_{2}=I_{2m}\sin \omega t}$ совпадают по фазе.

Два переменных синусоидальных тока сдвинуты по фазе относительно друг друга, если они имеют различные фазы.

На правой иллюстрации токи ${\displaystyle i_{1}=I_{1m}\sin(\omega t+{\frac {\pi }{2}})}$ и ${\displaystyle i_{2}=I_{2m}\sin {\omega t}}$ сдвинуты по фазе на угол ${\displaystyle {\frac {\pi }{2}}}$ , так как

${\displaystyle (\omega t+{\frac {\pi }{2}})-{\omega t}={\frac {\pi }{2}}}$ .

Ток ${\displaystyle i_{1}}$ опережает по фазе ток ${\displaystyle i_{2}}$ на угол ${\displaystyle {\frac {\pi }{2}}}$ , или, иначе, ток ${\displaystyle i_{2}}$ отстаёт по фазе относительно тока ${\displaystyle i_{1}}$ на угол ${\displaystyle {\frac {\pi }{2}}}$ .

Трёхфазный ток

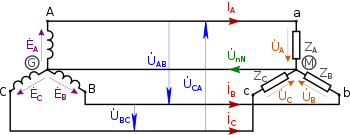
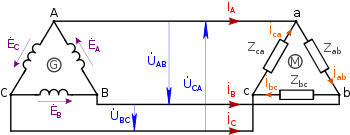
Среди многофазных систем переменного синусоидального тока наиболее широкое применение получила трёхфазная система электроснабжения .

Трёхфазной системой называется совокупность трёх однофазных электрических цепей, в которых действуют три электродвижущие силы одинаковой частоты, сдвинутые по фазе относительно друг друга на угол ${\displaystyle 120^{\circ }}$ ${\displaystyle \left({\frac {2}{3}}\pi \right)}$ .

Статор трёхфазного генератора переменного тока имеет три совершенно одинаковые катушки , размещённые на общем кольцеобразном ( тороидальном ) магнитопроводе , сдвинутые относительно друг друга на 120°. В обмотках индуктируются синусоидальные электродвижущие силы , сдвинутые по фазе относительно друг друга на 120°.

Если в первой катушке индуктируется электродвижущая сила ${\displaystyle e_{1}=E_{1m}\sin(\omega t)}$ ,

то во второй катушке будет индуктироваться электродвижущая сила ${\displaystyle e_{2}=E_{2m}\sin(\omega t-{\frac {2}{3}}\pi)}$ ,

в третьей катушке — электродвижущая сила ${\displaystyle e_{3}=E_{3m}\sin(\omega t-{\frac {4}{3}}\pi)}$ ,

где ${\displaystyle e_{1}}$ , ${\displaystyle e_{2}}$ и ${\displaystyle e_{3}}$ — мгновенные значения электродвижущих сил в отдельных катушках;

${\displaystyle E_{1m}}$ , ${\displaystyle E_{2m}}$ и ${\displaystyle E_{3m}}$ — амплитуды электродвижущих сил в отдельных катушках.

Если к каждой катушке подключить нагрузку, то в этих цепях будут протекать следующие токи:

${\displaystyle ~\mathrm {{\begin{matrix}{\mbox{i}}_{1}=I_{1m}\sin(\omega t-\psi _{1})\\{\mbox{i}}_{2}=I_{2m}\sin(\omega t-{\frac {2}{3}}\pi -\psi _{2})\\{\mbox{i}}_{3}=I_{3m}\sin(\omega t-{\frac {4}{3}}\pi -\psi _{3})\\\end{matrix}}{\Bigg \}}} }$ ,

где ${\displaystyle i_{1}}$ , ${\displaystyle i_{2}}$ и ${\displaystyle i_{3}}$ — мгновенные значения токов в первой, второй и третьей катушках;

${\displaystyle I_{1m}}$ , ${\displaystyle I_{2m}}$ и ${\displaystyle I_{3m}}$ — амплитуды токов в катушках;

${\displaystyle \psi _{1}}$ , ${\displaystyle \psi _{2}}$ и ${\displaystyle \psi _{3}}$ — углы сдвига фаз между электродвижущими силами и токами в катушках.

Трёхфазная система называется симметричной , если амплитуды электродвижущих сил в отдельных фазах генератора одинаковы по величине, то есть: ${\displaystyle E_{1m}=E_{2m}=E_{3m}=E_{m}}$ .

Если в трёхфазной системе отдельные фазы представляют собой совершенно независимые друг от друга электрические цепи , то такая система называется электрически не связанной , имеет мало преимуществ по сравнению с однофазной системой, практического применения не находит.

Трёхфазная система называется электрически связанной , если её отдельные фазы соединены между собой электрически.

Трёхфазная электрически связанная система обладает преимуществами по сравнению с однофазной системой, так как она требует меньшей затраты металла на провода при передаче одной и той же мощности.

Другое преимущество трёхфазной системы — возможность получения вращающегося магнитного поля , с помощью которого осуществляется работа простых по конструкции и удобных в эксплуатации асинхронных двигателей .

Для работы конденсаторных , однофазных и двухфазных асинхронных двигателей также используется вращающееся магнитное поле, однако их характеристики уступают трёхфазным асинхронным двигателям.

Трёхфазные системы как генератора, так и потребителя могут быть соединены «звездой» с нейтральным проводом, «звездой» без нейтрального провода или «треугольником».

• Соединение «звездой» с нейтральным проводом — четырёхпроводное, нейтральный провод обеспечивает независимость работы только одной фазы потребителя от другой фазы, так как при малом падении напряжения в проводах напряжения на фазах потребителя относительно мало изменяются с изменением нагрузки фаз. Применяется при неравномерной нагрузке на фазы.
• Соединение «звездой» без нейтрального провода — трёхпроводное, если результирующий ток в нейтральном проводе равен нулю, то отпадает необходимость в нём, что даёт экономию цветных металлов при передаче одной и той же мощности потребителю. Трёхфазная трёхпроводная система, соединённая «звездой», может применяться там, где нагрузка на фазы равномерна, например, при подключении трёхфазного асинхронного двигателя.

Если при трёхфазной трёхпроводной системе, соединённой «звездой», нагрузка оказывается неравномерной, то это ведёт к перераспределению напряжений на фазах потребителя в соответствии с их нагрузками и система перестаёт быть симметричной.

Например, если одну фазу потребителя « закоротить », то есть её напряжение станет равным нулю, то на остальных фазах напряжение возрастёт в ${\displaystyle {\sqrt {3}}}$ против нормального. Это явление называется « перекос фаз ». В бытовых условиях «перекос фаз» происходит, например, когда в домашнем распределительном щите по какой-то причине отсоединяется нулевой провод.

• Соединение «треугольником» — трёхпроводное. Применяется в основном потребителями с целью увеличения крутящего момента трёхфазного асинхронного двигателя, соответственно увеличивается его электрическая мощность при неизменном числе оборотов. Обмотки переключаются с «звезды» на «треугольник».

Или наоборот, когда необходимо электродвигатель (соединение обмоток «звезда»), рассчитанный, например, на напряжение 380 В включить под напряжение 220 В, в этом случае (обмотки также переключаются с «звезды» на «треугольник») его электрическая мощность и крутящий момент остаются неизменными.

Двухфазный ток

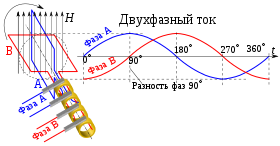
Двухфазным электрическим током называется совокупность двух однофазных токов, сдвинутых по фазе относительно друг друга на угол ${\displaystyle {\frac {\pi }{2}}}$ или на 90°.

Если две обмотки расположить в пространстве так, чтобы их оси были взаимно перпендикулярны и эти обмотки питать двухфазным синусоидальным током, то в системе возникнут два взаимноперпендикулярных магнитных потока . Вектор суммарного магнитного поля будет вращаться с постоянной угловой скоростью , равной частоте питающего напряжения. При этом возникает вращающееся магнитное поле . Ротор выполненный в виде короткозамкнутого « беличьего колеса » или представляющий собой металлический цилиндр связанный с валом , будет вращаться, производя механическую работу.

Частота вращения двухфазного асинхронного двигателя, как и асинхронного трёхфазного двигателя , будет несколько меньше частоты вращения вращающегося магнитного поля и зависит от нагрузки на валу — при её увеличении скорость вращения двигателя снижается. Разность частот питающего тока и частотой вращения называют частотой скольжения.

Действующее значение переменного синусоидального тока

Если все положительные и отрицательные мгновенные значения переменного синусоидального тока сложить, то их сумма будет равна нулю. Но если алгебраическая сумма всех мгновенных значений за период равна нулю, то и среднее значение этого тока за период также равно нулю: ${\displaystyle I_{avg}(T)=0}$ .

Среднее значение синусоидального тока за период не может служить для измерения этого тока.

Чтобы судить о величине переменного синусоидального тока, переменный ток сравнивают с постоянным током по их тепловому действию.

Закон Джоуля — Ленца

Количество теплоты ${\displaystyle Q}$ , выделяемое в единицу времени ${\displaystyle t}$ в рассматриваемом участке электрической цепи , пропорционально произведению квадрата силы тока ${\displaystyle I}$ на этом участке и электрического сопротивления ${\displaystyle R}$ участка цепи.

Количество теплоты в Джоулях : ${\displaystyle Q=I^{2}{Rt}}$ ;

Количество теплоты в калориях : ${\displaystyle Q={0,24}\times I^{2}{Rt}}$ , где

${\displaystyle I}$ — сила тока, Ампер ;

${\displaystyle R}$ — электрическое сопротивление, Ом ;

${\displaystyle t}$ — время в секундах .

Два тока, один из которых синусоидальный, а другой постоянный , эквивалентны по тепловому действию, если они, протекая по одинаковым сопротивлениям , за одинаковые отрезки времени выделяют одинаковое количество тепла.

Действующее значение переменного синусоидального тока численно равно току постоянному, эквивалентному данному синусоидальному току, то есть выделяющему порознь с ним в одинаковом сопротивлении за одинаковый отрезок времени одинаковое количество тепла.

Найдено экспериментально, а затем подтверждено теоретически, что величина действующего значения переменного синусоидального тока находится в строго определённой зависимости от амплитуды этого тока: ${\displaystyle I={\frac {I_{m}}{\sqrt {2}}}}$ , то есть действующее значение ${\displaystyle I}$ переменного синусоидального тока в ${\displaystyle {\sqrt {2}}}$ раз меньше амплитуды этого тока.

Амперметр электромагнитной или электродинамической системы , включенный в цепь переменного синусоидального тока, показывает действующее значение тока.

Аналогично действующему значению переменного синусоидального тока можно говорить о действующем значении переменной синусоидальной электродвижущей силы или переменного синусоидального напряжения .

Действующее значение напряжения в ${\displaystyle {\sqrt {2}}}$ меньше его амплитуды: ${\displaystyle U={\frac {U_{m}}{\sqrt {2}}}}$ или ${\displaystyle U_{m}={\sqrt {2}}\times U}$ .

Вольтметр электромагнитной или электродинамической системы , включенный в сеть переменного синусоидального тока, показывает действующее значение синусоидального напряжения.

Например, в электрической розетке электрическое напряжение ${\displaystyle \thicksim {220}~B}$ , так как это действующее значение, амплитудное напряжение будет ${\displaystyle {220}\times {1,41}={311}}$ Вольт .

Данные формулы справедливы только для синусоидального тока, если импульсы будут треугольной, пилообразной, прямоугольной или иной формы — требуется другая методика вычисления.

---

Методом математического анализа можно определить среднее значение переменного синусоидального тока за половину периода, например за положительную полуволну синусоиды.

Среднее значение переменного синусоидального тока за половину периода равно ${\displaystyle {\frac {I}{I_{avg}\left({\frac {T}{2}}\right)}}={{\frac {2}{\pi }}I_{m}}={0,637}\;I_{m}}$ .

Также можно определить отношение ${\displaystyle k}$ действующего значения тока к среднему за половину периода (положительную полуволну). Это отношение для синусоидального тока равно:

${\displaystyle k={\frac {I}{I_{avg}\left({\frac {T}{2}}\right)}}={\frac {\frac {I_{m}}{\sqrt {2}}}{{\frac {2}{\pi }}I_{m}}}={\frac {\pi }{2{\sqrt {2}}}}={1,11}}$ .

Генерирование переменного тока

Принцип действия генератора переменного тока основан на законе электромагнитной индукции — индуцировании электродвижущей силы в проволочном контуре ( проволочной рамке ), находящейся в однородном вращающемся магнитном поле .

---

Электродвижущая сила ${\displaystyle e}$ генератора переменного тока определяется по формуле:

${\displaystyle e=w2Bl{\frac {\alpha }{2}}\omega \sin \omega t}$ , где

${\displaystyle w}$ — количество витков;

${\displaystyle B}$ — магнитная индукция магнитного поля в вольт - секундах на квадратный метр ( Тл , Тесла );

${\displaystyle l}$ — длина каждой из активных сторон контура в метрах ;

${\displaystyle \omega }$ — угловая скорость синусоидальной электродвижущей силы, в данном случае равная угловой скорости вращения магнита в контуре;

${\displaystyle \omega t}$ — фаза синусоидальной электродвижущей силы.

---

Частота переменного тока, вырабатываемого генератором, определяется по формуле:

${\displaystyle f=p{\frac {n}{60}}}$ , где

${\displaystyle f}$ — частота в герцах ;

${\displaystyle n}$ — число оборотов ротора в минуту ;

${\displaystyle p}$ — число пар полюсов.

---

По количеству фаз генераторы переменного тока бывают:

• трёхфазные генераторы — основной тип мощных промышленных генераторов;
  См. также трёхфазная система электроснабжения , трёхфазный двигатель , автомобильный генератор трёхфазного переменного тока .
• однофазные генераторы, применяются, как правило, на маломощных бензиновых электростанциях , встроены в двигатели внутреннего сгорания мопедов , лёгких мотоциклов , снегоходов , гидроциклов , подвесные лодочные моторы ;
  См. также конденсаторный двигатель , однофазный двигатель .
• двухфазные генераторы, встречаются значительно реже по сравнению с однофазными и трёхфазными.
  См. также двухфазная электрическая сеть , двухфазный двигатель .

Инверторы

Постоянный ток может быть преобразован в переменный с помощью инвертора .

Недорогие модели инверторов имеют на выходе переменный ток несинусоидальной формы, обычно прямоугольные импульсы или модифицированная синусоида . Для получения синусоидального тока инвертор должен иметь задающий генератор (как правило, специализированная микросхема , формирующая электрический сигнал синусоидальной формы, который затем управляет работой тиристорных или транзисторных электронных ключей ).

Фазорасщепитель

Трёхфазный ток может быть получен из однофазного при помощи фазорасщепителя . Эти электрические машины применяются, в частности, на электровозах , таких как ВЛ60 , ВЛ80 .

Сети переменного тока

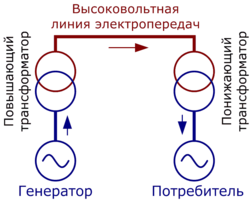
Производители электроэнергии ( ГЭС , ТЭС , ТЭЦ , атомные и другие электростанции ) генерируют переменный ток промышленной частоты (в России — 50 Гц), напряжением порядка 10 — 20 кВ.

Затем электрический ток поступает на трансформаторные подстанции , которые находятся рядом с электростанциями, где происходит повышение электрического напряжения .

Переменный ток высокого напряжения передаётся потребителям по линиям электропередачи (ЛЭП). Повышение напряжения необходимо для того, чтобы уменьшить потери в проводах ЛЭП (см. Закон Джоуля — Ленца , при увеличении электрического напряжения уменьшается сила тока в электрической цепи, соответственно уменьшаются тепловые потери) .

Самая высоковольтная в мире ЛЭП Экибастуз-Кокчетав работала под напряжением 1 миллион 150 тысяч вольт.

На другом конце линии электропередачи находится понижающая трансформаторная подстанция, где высоковольтный переменный ток понижается трансформаторами до нужного потребителю значения.

В подавляющем большинстве случаев по линиям электропередачи передаётся трёхфазный ток , однако существуют линии электропередачи постоянного тока , например высоковольтная линия постоянного тока Волгоград-Донбасс , высоковольтная линия постоянного тока Экибастуз-Центр , материковая Южная Корея — остров Чеджудо и другие. Использование постоянного тока позволяет увеличить передаваемую электрическую мощность , передавать электроэнергию между энергосистемами , использующими переменный ток разной частоты, например, 50 и 60 герц, а также не синхронизировать соседние энергосистемы, как это сделано на границе Ленинградской области с Финляндией (см. вставка постоянного тока Выборг — Финляндия ) .

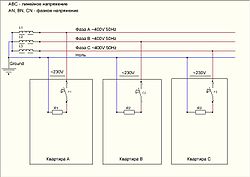
В России в электрических сетях общего назначения используется трёхфазный ток с межфазным напряжением 380 Вольт .

Качество электрической энергии — её электрическое напряжение и частота должны строго соблюдаться.

К жилым домам (на сельские улицы) подводятся четырёхпроводные (три фазовых провода и один нейтральный (нулевой) провод ) линии электропередачи (воздушные или кабельные ЛЭП) с межфазным напряжением 380 вольт (с 2003 года 400 Вольт по ГОСТ 29322-2014). В отдельную квартиру (или в сельский дом) подводится фазовый провод и нулевой провод, электрическое напряжение между «фазой» и «нулём» составляет 220 вольт (с 2003 года 230 Вольт по ГОСТ 29322-2014). Определить, где какой провод можно с помощью индикатора фазы .

Например, в первую квартиру подводится фаза «A», во вторую квартиру — фаза «B», в третью квартиру — фаза «C» и так далее…

Электрификация железных дорог на переменном токе

В России и в республиках бывшего СССР около половины всех железных дорог электрифицировано на однофазном переменном токе частотой 50 Гц. Напряжение ~ 25 кВ (обычно до 27,5 кВ, с учётом потерь) подаётся на контактный провод , вторым (обратным) проводом служат рельсы . Также проводится электрификация по системе 2 × 25 кВ (два по двадцать пять киловольт) , когда на отдельный питающий провод подаётся напряжение ~ 50 кВ (обычно до 55 кВ, с учётом потерь) , а на контактный провод от автотрансформаторов подаётся половинное напряжение от 50 кВ (то есть 25 кВ) . Электровозы и электропоезда переменного тока при работе на участках 2 × 25 кВ в переделке не нуждаются.

Проводится политика на дальнейшее расширение полигона тяги переменного тока как за счёт вновь электрифицируемых участков, так и за счёт перевода некоторых линий с постоянного тока на переменный ток. Переведены в 1990-е — 2000-е годы:

• на Восточно-Сибирской железной дороге : участок Слюдянка — Иркутск — Зима ;
• на Октябрьской железной дороге : участок Лоухи — Мурманск ;
• на Приволжской железной дороге : Саратовский и Волгоградский железнодорожные узлы ;
• на Северо-Кавказской железной дороге : участки Минеральные Воды — Кисловодск и Бештау — Железноводск .

Также выпускаются двухсистемные электровозы, способные работать как на переменном, так и на постоянном токе (см. ВЛ61 Д , ВЛ82 и ВЛ82 М , ЭП10 , ЭП20 ).

См. также

• Электрический ток
• Постоянный ток
• Действующее значение переменного тока
• Список параметров напряжения и силы электрического тока
• Трёхфазный ток
• Реактивное сопротивление
• Токи высокой частоты
• Векторная диаграмма
• Стандарты напряжений и частот в разных странах

Примечания

Ссылки