Interested Article - Сферические теоремы косинусов

melania
  • 2020-01-18
  • 1

Сферический треугольник.

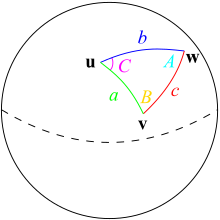
Первая и вторая сферические теоремы косинусов устанавливают соотношения между сторонами и противолежащими им углами сферического треугольника .

Формулировка

Теоремы косинусов для сферического треугольника со сторонами a , b , c и углами A , B , C имеют следующий вид:

cos ⁡ c = cos ⁡ a cos ⁡ b + sin ⁡ a sin ⁡ b cos ⁡ C , {\displaystyle \cos c=\cos a\cos b+\sin a\sin b\cos C,}
cos ⁡ A = − cos ⁡ B cos ⁡ C + sin ⁡ B sin ⁡ C cos ⁡ a . {\displaystyle \cos A=-\cos B\cos C+\sin B\sin C\cos a.}

Эти две теоремы двойственны по отношению друг к другу, поскольку углы и стороны всякого сферического треугольника дополняются до развёрнутого угла сторонами и углами соответствующего полярного треугольника . Поэтому достаточно доказать одну из них.

Доказательство
Рисунок к доказательству теоремы косинусов с помощью проекций.

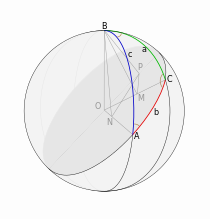
Доказательство проведём с помощью проекций . На рисунке показан сферический треугольник ABC на сфере радиуса R с центром в точке O . BP — перпендикуляр к плоскости большого круга, проходящего через сторону b , BM — перпендикуляр к OC , BN — перпендикуляр к OA . По утверждению, обратному теореме о трёх перпендикулярах , PM — перпендикуляр к OC , PN — перпендикуляр к OA . Заметим, что угол PMB равен π - C, кроме того, ON = R cos c и OM = R cos a. Далее, проецируем ломаную OMPN на прямую, содержащую ON .

pr O N = pr O M + pr M P + pr P N {\displaystyle {\mbox{pr }}ON={\mbox{pr }}OM+{\mbox{pr }}MP+{\mbox{pr }}PN} ,
P N ⊥ O A ⇒ pr P N = 0 {\displaystyle PN\perp OA\Rightarrow {\mbox{pr }}PN=0} ,
pr O M = O M cos ⁡ b = R cos ⁡ a cos ⁡ b {\displaystyle {\mbox{pr }}OM=OM\cos b=R\cos a\cos b} ,
pr M P = P M cos ⁡ ( π − ( π 2 − ∠ M P N ) ) = P M ( − sin ⁡ ∠ M P N ) {\displaystyle {\mbox{pr }}MP=PM\cos(\pi -({\frac {\pi }{2}}-\angle MPN))=PM(-\sin \angle MPN)}
= B M cos ⁡ ∠ P M B ( − sin ⁡ b ) = B M cos ⁡ ( π − C ) ( − sin ⁡ b ) = R sin ⁡ b sin ⁡ a cos ⁡ C {\displaystyle =BM\cos \angle PMB(-\sin b)=BM\cos(\pi -C)(-\sin b)=R\sin b\sin a\cos C} .

Подставляем три последних выражения и указанное выше выражение ON = R cos c в первое выражение и получаем:

cos ⁡ c = cos ⁡ a cos ⁡ b + sin ⁡ a sin ⁡ b cos ⁡ C {\displaystyle \cos c=\cos a\cos b+\sin a\sin b\cos C} .

Теоремы косинусов для двух других сторон, то есть теорему для cos a и теорему для cos b, получаем аналогично, их также можно получить сразу из формулы для стороны c при помощи круговой перестановки букв:

a → b → c → a , A → B → C → A {\displaystyle a\rightarrow b\rightarrow c\rightarrow a,A\rightarrow B\rightarrow C\rightarrow A}

Сферический треугольник для определения кратчайшего расстояния между точками на Земле.

Следствия и применение

Если угол C — прямой, первая теорема косинусов переходит в сферическую теорему Пифагора :

cos ⁡ c = cos ⁡ a cos ⁡ b . {\displaystyle \cos c=\cos a\cos b.}

Хотя для решения косоугольных сферических треугольников обычно используются более удобные формулы, с помощью теоремы косинусов выводится важная для геодезии формула длины ортодромии — кратчайшего расстояния между точками на земной поверхности с известными координатами (в предположении сферичности Земли). Обозначим географические широты двух данных точек φ A {\displaystyle \varphi _{A}} и φ B {\displaystyle \varphi _{B}} , разность долгот — Δ λ A B {\displaystyle \Delta \lambda _{AB}} , кратчайшее расстояние между ними обозначим d, длину дуги в 1 градус — a. Тогда формула длины ортодромии :

cos ⁡ ( d a ) = sin ⁡ φ A ⋅ sin ⁡ φ B + cos ⁡ φ A ⋅ cos ⁡ φ B ⋅ cos ⁡ Δ λ A B {\displaystyle \cos \left({\frac {d}{a}}\right)=\sin \varphi _{A}\cdot \sin \varphi _{B}+\cos \varphi _{A}\cdot \cos \varphi _{B}\cdot \cos \Delta \lambda _{AB}}

Эта формула сразу получается применением теоремы косинусов к стороне AB сферического треугольника P n AB. Подобная формула справедлива для любой сферической поверхности и поэтому её можно применять также для определения углового расстояния между звёздами по известным их экваториальным координатам .

Пример 1: определение углового расстояния между двумя светилами на небесной сфере

Определим угловое расстояние (x) между звездой δ Цефея (экваториальные координаты: α 1 =22ч 29м, δ 1 =+58° 25′) и галактикой Туманность Андромеды (α 2 =0ч 43м, δ 2 =+41° 16′) на небесной сфере. Выражаем α 1 в градусах и долях градуса:

α 1 = ( 22 + 29 60 ) ⋅ 360 24 = 337 ∘ , 25 {\displaystyle \alpha _{1}=\left(22+{\frac {29}{60}}\right)\cdot {\frac {360}{24}}=337^{\circ },25}

Аналогично получаем, что α 2 =10°,75. Выражаем δ 1 в градусах и долях градуса:

δ 1 = 58 + 25 60 = 58 ∘ , 42 {\displaystyle \delta _{1}=58+{\frac {25}{60}}=58^{\circ },42}

Аналогично δ 2 =41°,27. Применяем теорему косинусов :

cos ⁡ x = cos ⁡ ( 90 ∘ − δ 1 ) ⋅ cos ⁡ ( 90 ∘ − δ 2 ) + sin ⁡ ( 90 ∘ − δ 1 ) ⋅ sin ⁡ ( 90 ∘ − δ 2 ) ⋅ cos ⁡ ( α 1 − α 2 ) = sin ⁡ 58 ∘ , 42 ⋅ sin ⁡ 41 ∘ , 27 + cos ⁡ 58 ∘ , 42 ⋅ cos ⁡ 41 ∘ , 27 ⋅ cos ⁡ ( 337 ∘ , 25 − 10 ∘ , 75 ) = 0 , 89 {\displaystyle {\begin{aligned}\cos x&=\cos(90^{\circ }-\delta _{1})\cdot \cos(90^{\circ }-\delta _{2})+\sin(90^{\circ }-\delta _{1})\cdot \sin(90^{\circ }-\delta _{2})\cdot \cos(\alpha _{1}-\alpha _{2})\\&=\sin 58^{\circ },42\cdot \sin 41^{\circ },27+\cos 58^{\circ },42\cdot \cos 41^{\circ },27\cdot \cos(337^{\circ },25-10^{\circ },75)\\&=0,89\end{aligned}}}

Отсюда x=27°,11.

Теорема косинусов в её втором виде (соотношение между тремя углами и стороной) может быть применена для вычисления взаимного наклонения двух орбит при известном наклонении каждой орбиты к какой-то другой плоскости. Например, по этой формуле можно вычислить наклонение орбиты Плутона к орбите Нептуна , используя наклонения их орбит к эклиптике и долготы их восходящих узлов.

Пример 2: определение взаимного наклонения орбит небесных тел

Определим взаимное наклонение (x) орбит Плутона (наклонение орбиты к эклиптике — 17°,14, долгота восходящего узла — 110°,30) и Нептуна (наклонение орбиты к эклиптике — 1°,77, долгота восходящего узла — 131°,79). В соответствующем сферическом треугольнике известны два угла: один равен наклонению орбиты Плутона к эклиптике, другой — дополнению наклонения орбиты Нептуна к эклиптике до 180 градусов. Известна также прилегающая к этим углам сторона, равная разности долгот восходящих узлов Плутона и Нептуна. Осталось применить второй вариант теоремы косинусов — для углов:

cos ⁡ x = − cos ⁡ ( 17 ∘ , 14 ) ⋅ cos ⁡ ( 180 ∘ − 1 ∘ , 77 ) + sin ⁡ ( 17 ∘ , 14 ) ⋅ sin ⁡ ( 180 ∘ − 1 ∘ , 77 ) ⋅ cos ⁡ ( 131 ∘ , 79 − 110 ∘ , 30 ) ≈ 0 , 9636 {\displaystyle {\begin{aligned}\cos x&=-\cos(17^{\circ },14)\cdot \cos(180^{\circ }-1^{\circ },77)+\sin(17^{\circ },14)\cdot \sin(180^{\circ }-1^{\circ },77)\cdot \cos(131^{\circ },79-110^{\circ },30)\\&\approx 0,9636\\\end{aligned}}}

Отсюда x≈15°,51.

История

Основная статья: История тригонометрии

Математики средневекового Востока использовали утверждение, равносильное сферической теореме косинусов, при решении конкретных астрономических задач. Эти соотношения, используемые при определении высоты Солнца, встречаются в сочинениях Сабита ибн Корры , ал-Махани , ал-Баттани , Ибн Юниса , ал-Бируни .

Первая явная формулировка теоремы дана в XV веке Региомонтаном , который назвал её «теоремой Альбатегния» (по латинизированному имени ал-Баттани ).

См. также

Примечания

  1. Приводится по изданию: Степанов Н. Н. Формулы косинуса стороны // . — М. — Л. : ОГИЗ , 1948. — С. —28. — 154 с.
  2. Михайлов В.С., Кудрявцев В.Г., Давыдов В.С. 26.2. Основные формулы ортодромии. Способы её задания // . — Киев, 2009. 25 июля 2012 года.
  3. Меёс Ж. 9. Угловое расстояние между объектами // Астрономические формулы для калькуляторов. — Мир , 1988. — С. 44—46. — 168 с. — ISBN 5030009361 .
  4. Lee Kai Ming. . — 2010. — С. 6 . 3 декабря 2008 года.

Литература

  • Вентцель М. К. Сферическая тригонометрия. 2-е изд., ИГКЛ, 1948, 115с.
  • Матвиевская Г. П. Очерки истории тригонометрии: Древняя Греция. Средневековый Восток. Позднее Средневековье. — Изд. 2-е. — М. : Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9 .
  • Степанов Н. Н. Сферическая тригонометрия. — Л.-М., 1948.

melania
  • 2020-01-18
  • 1

Same as Сферические теоремы косинусов

The title for the last searches