Interested Article - DSA

DSA ( англ. Digital Signature Algorithm — алгоритм цифровой подписи ) — криптографический алгоритм с использованием закрытого ключа (из пары ключей: <открытый; закрытый>) для создания электронной подписи , но не для шифрования (в отличие от RSA и схемы Эль-Гамаля ). Подпись создается секретно (закрытым ключом), но может быть публично проверена (открытым ключом). Это означает, что только один может создать подпись сообщения, но любой может проверить её корректность. Алгоритм основан на вычислительной сложности взятия логарифмов в конечных полях .

Алгоритм был предложен Национальным институтом стандартов и технологий ( США ) в августе 1991 и является запатентованным (автор патента — David W. Kravitz), НИСТ сделал этот патент доступным для использования без лицензионных отчислений . DSA является частью DSS ( англ. Digital Signature Standard — стандарт цифровой подписи), впервые опубликованного 15 декабря 1998 (документ FIPS-186 ( англ. Federal Information Processing Standards — федеральные стандарты обработки информации)). Стандарт несколько раз обновлялся , последняя версия FIPS-186-4 . (июль 2013).

Описание алгоритма

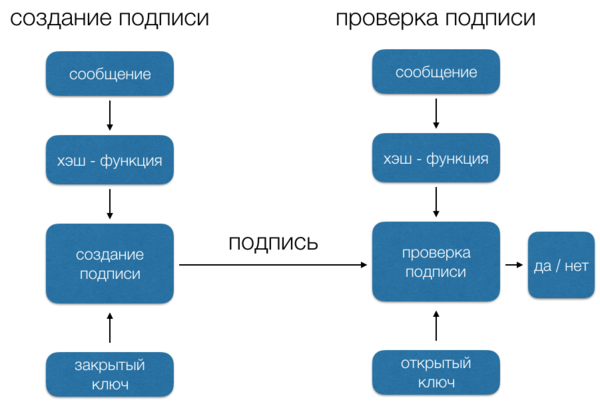
DSA включает в себя два алгоритма (S, V): для создания подписи сообщения (S) и для ее проверки (V).

Оба алгоритма вначале вычисляют хеш сообщения, используя криптографическую хеш-функцию . Алгоритм S использует хеш и секретный ключ для создания подписи, алгоритм V использует хеш сообщения, подпись и открытый ключ для проверки подписи.

Стоит подчеркнуть, что фактически подписывается не сообщение (произвольной длины), а его хеш (160 - 256 бит), поэтому неизбежны коллизии и одна подпись, вообще говоря, действительна для нескольких сообщений с одинаковым хешем. Поэтому выбор достаточно "хорошей" хеш-функции очень важен для всей системы в целом. В первой версии стандарта использовалась хеш-функция SHA-1 ( англ. Secure Hash Algorithm - безопасный алгоритм хеширования) , в последней версии также можно использовать любой алгоритм семейства SHA-2 . В августе 2015 был опубликован FIPS-202 , описывающий новую хеш-функцию SHA-3 . Но на сегодняшний день она не включена в стандарт DSS .

Для работы системы требуется база соответствия между реальными реквизитами автора (это может быть как частное лицо, так и организация) и открытыми ключами , а также всеми необходимыми параметрами схемы цифровой подписи (хеш-функция, простые числа ). Например, подобной базой может служить центр сертификации .

Параметры схемы цифровой подписи

Для построения системы цифровой подписи нужно выполнить следующие шаги:

Выбор криптографической хеш-функции H(x).
Выбор простого числа q , размерность которого N в битах совпадает с размерностью в битах значений хеш-функции H(x).
Выбор простого числа p , такого, что (p-1) делится на q . Битовая длина p обозначается L .
Выбор числа g ( $g\neq 1$ $g\neq 1$ ) такого, что его мультипликативный порядок по модулю p равен q . Для его вычисления можно воспользоваться формулой $g=h^{(p-1)/q}\mod p$ $g=h^{{(p-1)/q}}\mod p$ , где h — некоторое произвольное число, $h\in (1;p-1)$ $h\in (1;p-1)$ такое, что $g\neq 1$ $g\neq 1$ . В большинстве случаев значение h = 2 удовлетворяет этому требованию.

Как упомянуто выше, первоочередным параметром схемы цифровой подписи является используемая криптографическая хеш-функция , необходимая для преобразования текста сообщения в число , для которого и вычисляется подпись. Важной характеристикой этой функции является битовая длина выходной последовательности, обозначаемая далее N . В первой версии стандарта DSS рекомендована функция SHA-1 и, соответственно, битовая длина подписываемого числа 160 бит. Сейчас SHA-1 уже не является достаточно безопасной . В стандарте указаны следующие возможные пары значений чисел L и N :

L = 1024, N = 160
L = 2048, N = 224
L = 2048, N = 256
L = 3072, N = 256

В соответствии с этим стандартом рекомендованы хеш-функции семейства SHA-2 . Правительственные организации США должны использовать один из первых трех вариантов, центры сертификации должны использовать пару, которая равна или превосходит пару, используемую подписчиками . Проектирующий систему может выбрать любую допустимую хеш-функцию. Поэтому далее не будет заостряться внимание на использовании конкретной хеш-функции.

Стойкость криптосистемы на основе DSA не превосходит стойкость используемой хеш-функции и стойкость пары (L,N), чья стойкость не больше стойкости каждого из чисел по отдельности. Также важно учитывать, как долго система должна оставаться безопасной. В данный момент для систем, которые должны быть стойкими до 2010 ( 2030 ) года, рекомендуется длина в 2048 (3072) бита.

Открытый и секретный ключи

Секретный ключ представляет собой число $x\in (0,q)$ $x\in (0,q)$
Открытый ключ вычисляется по формуле $y=g^{x}\mod p$ $y=g^{x}\mod p$

Открытыми параметрами являются числа (p, q, g, y) . Закрытый параметр только один — число x . При этом числа (p, q, g) могут быть общими для группы пользователей, а числа x и y являются соответственно закрытым и открытым ключами конкретного пользователя. При подписывании сообщения используются секретные числа x и k , причем число k должно выбираться случайным образом (на практике псевдослучайным) при вычислении подписи каждого следующего сообщения.

Поскольку (p, q, g) могут быть использованы для нескольких пользователей, на практике часто делят пользователей по некоторым критериям на группы с одинаковыми (p, q, g) .

Подпись сообщения

Подпись сообщения выполняется по следующему алгоритму :

Выбор случайного числа $k\in (0,q)$ $k\in (0,q)$
Вычисление $r=(g^{k}\mod p)\mod q$ $r=(g^{k}\mod p)\mod q$
Выбор другого k, если $r=0$ $r=0$
Вычисление $s=k^{-1}(H(m)+x\cdot r)\mod q$ $s=k^{{-1}}(H(m)+x\cdot r)\mod q$
Выбор другого k, если $s=0$ $s=0$
Подписью является пара $(r,s)$ $(r,s)$ общей длины $2N$ $2N$

Вычислительно сложные операции это возведение в степень по модулю (вычисление $g^{k}{\bmod {p}}$ $g^{k}{\bmod {p}}$ ), для которого существуют быстрые алгоритмы , вычисление хеша $H(x)$ $H(x)$ , где сложность зависит от выбранного алгоритма хеширования и размера входного сообщения, и нахождение обратного элемента $k^{-1}{\bmod {q}}$ $k^{-1}{\bmod {q}}$ используя, например, расширенный алгоритм Евклида или малую теорему Ферма в виде $k^{-1}{\bmod {q}}=k^{q-2}{\bmod {q}}$ $k^{-1}{\bmod {q}}=k^{q-2}{\bmod {q}}$ .

Проверка подписи

Проверка подписи выполняется по алгоритму :

1 Вычисление  $w=s^{-1}\mod q$  $w=s^{{-1}}\mod q$  2 Вычисление  $u_{1}=H(m)\cdot w\mod q$  $u_{1}=H(m)\cdot w\mod q$  3 Вычисление  $u_{2}=r\cdot w\mod q$  $u_{2}=r\cdot w\mod q$  4 Вычисление  $v=(g^{u_{1}}\cdot y^{u_{2}}\mod p)\mod q$  $v=(g^{{u_{1}}}\cdot y^{{u_{2}}}\mod p)\mod q$  5 Подпись верна, если  $v=r$  $v=r$

При проверке вычислительно сложные операции это два возведения в степень $g^{u_{1}}y^{u_{2}}$ $g^{u_{1}}y^{u_{2}}$ , вычисление хеша $H(x)$ $H(x)$ и нахождение обратного элемента $s^{-1}{\bmod {q}}$ $s^{-1}{\bmod {q}}$ .

Корректность схемы

Данная схема цифровой подписи корректна в той степени, что желающий проверить подлинность подписи всегда получит положительный результат в случае подлинности. Покажем это:

Во-первых, если $g=h^{(p-1)/q}\mod p$ $g=h^{{(p-1)/q}}\mod p$ , то из этого по Малой теореме Ферма следует $g^{q}=h^{p-1}=1\mod p$ $g^{q}=h^{{p-1}}=1\mod p$ . Поскольку g >1 и q простое число, то g должно иметь мультипликативный порядок q по модулю p .

Для подписи сообщения вычисляется

s=k^{-1}(H(m)+x\cdot r)\mod {q}.

s=k^{{-1}}(H(m)+x\cdot r)\mod {q}.

Из этого следует

k=H(m)\cdot s^{-1}+x\cdot r\cdot s^{-1}=H(m)\cdot w+x\cdot r\cdot w\mod {q}.

k=H(m)\cdot s^{{-1}}+x\cdot r\cdot s^{{-1}}=H(m)\cdot w+x\cdot r\cdot w\mod {q}.

Так как g имеет порядок q , получим

g^{k}=g^{H(m)\cdot w\mod q}g^{x\cdot r\cdot w\mod q}=g^{H(m)\cdot w\mod q}y^{r\cdot w\mod q}=g^{u1}y^{u2}\mod {p}.

g^{k}=g^{{H(m)\cdot w\mod q}}g^{{x\cdot r\cdot w\mod q}}=g^{{H(m)\cdot w\mod q}}y^{{r\cdot w\mod q}}=g^{{u1}}y^{{u2}}\mod {p}.

Наконец, корректность схемы DSA следует из

r=(g^{k}\mod p)\mod q=(g^{u1}y^{u2}\mod p)\mod q=v.

r=(g^{k}\mod p)\mod q=(g^{{u1}}y^{{u2}}\mod p)\mod q=v.

Пример работы

Приведем пример работы алгоритма для небольших чисел. Пусть значение хеш - функции нашего сообщения $H=9$ $H=9$ .

Генерация параметров

$H=9_{10}=1001_{2}$ $H=9_{10}=1001_{2}$
длина хеша $4$ $4$ , значит можно выбрать $q=11_{10}=1011_{2}$ $q=11_{10}=1011_{2}$
выберем $p=23$ $p=23$ , так как $23-1=22=2*q$ $23-1=22=2*q$
выберем $g=2^{2}=4$ $g=2^{2}=4$

Создание ключей

в качестве секретного ключа выберем $x=7$ $x=7$
тогда открытый ключ $y=g^{x}{\bmod {p}}=4^{7}{\bmod {2}}3=16384{\bmod {2}}3=(712\cdot 23+8){\bmod {2}}3=8$ $y=g^{x}{\bmod {p}}=4^{7}{\bmod {2}}3=16384{\bmod {2}}3=(712\cdot 23+8){\bmod {2}}3=8$

Подпись сообщения

выберем $k=3$ $k = 3$
тогда $r=(g^{k}{\bmod {p}}){\bmod {q}}=(4^{3}{\bmod {2}}3){\bmod {1}}1=7$ $r=(g^{k}{\bmod {p}}){\bmod {q}}=(4^{3}{\bmod {2}}3){\bmod {1}}1=7$
$r\neq 0$ $r\neq 0$ , идем дальше
$s=k^{-1}(H(m)+x\cdot r){\bmod {q}}=4(9+7\cdot 7){\bmod {1}}1=1$ $s=k^{-1}(H(m)+x\cdot r){\bmod {q}}=4(9+7\cdot 7){\bmod {1}}1=1$ , где учтено, что $3^{-1}{\bmod {1}}1=4$ $3^{-1}{\bmod {1}}1=4$
$s\neq 0$ $s\neq 0$ , идем дальше
подписью является пара чисел $(r,s)=(7,1)$ $(r,s)=(7,1)$

Проверка подписи

$w=s^{-1}{\bmod {q}}=1^{-1}{\bmod {1}}1=1$ $w=s^{-1}{\bmod {q}}=1^{-1}{\bmod {1}}1=1$
$u_{1}=H(m)\cdot w{\bmod {q}}=9\cdot 1{\bmod {1}}1=9$ $u_{1}=H(m)\cdot w{\bmod {q}}=9\cdot 1{\bmod {1}}1=9$
$u_{2}=r\cdot w{\bmod {q}}=7\cdot 1{\bmod {1}}1=7$ $u_{2}=r\cdot w{\bmod {q}}=7\cdot 1{\bmod {1}}1=7$
$v=(g^{u_{1}}\cdot y^{u_{2}}{\bmod {p}}){\bmod {q}}=(4^{9}\cdot 8^{7}{\bmod {2}}3){\bmod {1}}1=7$ $v=(g^{u_{1}}\cdot y^{u_{2}}{\bmod {p}}){\bmod {q}}=(4^{9}\cdot 8^{7}{\bmod {2}}3){\bmod {1}}1=7$
получили, что $v=r$ $v = r$ , значит подпись верна.

Аналоги

Алгоритм DSA основывается на трудности вычисления дискретных логарифмов и является модификацией классической схемы Эль-Гамаля , где добавлено хеширование сообщения, а также все логарифмы вычисляются по $mod~q$ $mod~q$ , что позволяет сделать подпись короче по сравнению с аналогами . На основе схемы Эль-Гамаля построены и другие алгоритмы, например - российский ГОСТ 34.10-94 , который сейчас считается устаревшим. На смену ему пришел стандарт ГОСТ Р 34.10-2012 , в котором используется группа точек эллиптической кривой .

Подобная модификация, т.е. переход от мультипликативной группы по модулю простого числа к группе точек эллиптической кривой существует и для DSA - ECDSA ( англ. Elliptic Curve Digital Signature Algorithm - алгоритм цифровой подписи на эллиптических кривых). Он применяется, например, в криптовалюте bitcoin для подтверждения транзакций. Этот перевод позволяет уменьшить размер ключей без ущерба для безопасности - в системе bitcoin размер закрытого ключа 256 бит, а соответствующего ему открытого - 512 бит.

Другой распространенный алгоритм с открытым ключом (используется и для шифрования, и для цифровой подписи), RSA (назван в честь авторов: Ривест , Шамир , Адлеман ), основан на сложности факторизации больших чисел.

Криптографическая стойкость

Любую атаку на алгоритм можно описать так: злоумышленник получает все открытые параметры подписи и некий набор пар (сообщение, подпись) и пытается, используя этот набор, создать действительную подпись для нового сообщения, не представленного в наборе.

Эти атаки можно условно разделить на две группы - во-первых, злоумышленник может попытаться восстановить секретный ключ $x$ $x$ , и тогда он сразу получает возможность подписать любое сообщение, во-вторых, он может попробовать создать действительную подпись для нового сообщения без прямого восстановления секретного ключа.

Предсказуемость случайного параметра

Равномерное распределение случайного параметра $k$ $k$ очень важно для безопасности системы. Если известны несколько последовательных бит параметра $k$ $k$ для ряда подписей, то секретный ключ возможно восстановить с высокой вероятностью.

Повторение параметра для двух сообщений ведет к простому взлому системы. Это может произойти при использовании плохого генератора псевдослучайных чисел . Данная уязвимость в системе PlayStation 3 позволяла подписывать от имени Sony любые программы. В некоторых реализациях системы bitcoin для Android злоумышленник мог получить доступ к кошельку. В обоих примерах использовалась система ECDSA .

Если для двух сообщений $m_{1},m_{2}$ $m_{1},m_{2}$ использовался один и тот же параметр $k$ $k$ , тогда их подписи $(r,s)$ $(r,s)$ будут иметь одинаковые $r$ $r$ , но разные $s$ $s$ , назовем их $s_{1},s_{2}$ $s_{1},s_{2}$ .

Из выражения для $s$ $s$ можно выразить общий $k$ $k$ :

$k=(H(m)+xr)s^{-1}\mod q$ $k=(H(m)+xr)s^{-1}\mod q$ .

И приравнять общий $k$ $k$ для разных сообщений:

$(H(m_{1})+xr)s_{1}^{-1}\mod q=(H(m_{2})+xr)s_{2}^{-1}\mod q$ $(H(m_{1})+xr)s_{1}^{-1}\mod q=(H(m_{2})+xr)s_{2}^{-1}\mod q$

Отсюда легко выразить секретный ключ $x$ $x$ :

$x={\frac {H(m_{1})s_{1}^{-1}-H(m_{2})s_{2}^{-1}}{r(s_{2}^{-1}-s_{1}^{-1})}}$ $x={\frac {H(m_{1})s_{1}^{-1}-H(m_{2})s_{2}^{-1}}{r(s_{2}^{-1}-s_{1}^{-1})}}$

Existential forgery

На некоторые алгоритмы цифровой подписи возможна атака существующей подделки . Она заключается в том, что для подписи (либо вообще случайной, либо созданной по некоторому правилу) возможно создать корректное сообщение (которое, правда, обычно не несет смысла), используя только открытые параметры.

Для схемы DSA подпись $r=g^{e}y\mod p\mod q$ $r=g^{e}y\mod p\mod q$ , $s=r$ $s=r$ при любом $e$ $e$ корректна для сообщения с хешем $H(m)=es$ $H(m)=es$ .

Это одна из причин хеширования входного сообщения. При корректном выборе хеш-функции алгоритм DSA защищен от этой атаки, потому что обращение криптографической хеш-функции (т.е. для заданного $k$ $k$ нахождение $m$ $m$ такого, что $H(m)=k$ $H(m)=k$ ) является вычислительно сложной задачей.

Восстановление ключа

условие корректности подписи можно переписать в ином виде:

$g^{ks}\mod p\mod q=g^{H(m)+xr}\mod p\mod q$ $g^{ks}\mod p\mod q=g^{H(m)+xr}\mod p\mod q$

это уравнение эквивалентно (т.к. мультипликативный порядок g по модулю p равен q)

$H(m)\mod q=ks-xr\mod q$ $H(m)\mod q=ks-xr\mod q$

значит можно считать, что злоумышленнику для восстановления ключа требуется решить систему уравнений вида

$H(m_{i})\mod q=k_{i}s_{i}-xr_{i}\mod q$ $H(m_{i})\mod q=k_{i}s_{i}-xr_{i}\mod q$

но в этой системе неизвестен $x$ $x$ и все $k_{i}$ $k_i$ , значит число неизвестных на единицу больше, чем уравнений и при любом $x$ $x$ найдутся $k_{i}$ $k_i$ , удовлетворяющие системе. Так как q - большое простое число, то для восстановления $x\mod q$ $x\mod q$ потребуется экспоненциальное число пар (сообщение, подпись).

Подделка подписи

Можно попытаться подделать подпись, не зная секретный ключ, то есть попытаться решить уравнение

$r^{s}\mod p\mod q=g^{H(m)}y^{r}\mod p\mod q$ $r^{s}\mod p\mod q=g^{H(m)}y^{r}\mod p\mod q$

относительно $r$ $r$ и $s$ $s$ . При каждом фиксированном $r$ $r$ уравнение эквивалентно вычислению дискретного логарифма.

Система проверки реализации алгоритма

Условия лицензии позволяют реализовывать алгоритм программно и аппаратно. НИСТ создал ( англ. The Digital Signature Algorithm Validation System - система проверки алгоритма цифровой подписи ). DSAVS состоит из нескольких модулей проверки на соответствие стандарту, которые тестируют каждый компонент системы независимо от других. Тестируемые компоненты реализации:

Генерация доменных параметров
Проверка доменных параметров
Генерация пары открытый-закрытый ключ
Создание подписи
Проверка подписи

Для проверки реализации разработчик должен подать заявку на тестирование его реализации в CMT laboratory ( англ. Cryptographic Module Testing Laboratory - лаборатория тестирования криптографических модулей ).

Генерация простых чисел

При работе алгоритма DSA требуется два простых числа ( $p$ $p$ и $q$ $q$ ), следовательно необходим генератор простых или псевдопростых чисел.

Для генерации простых чисел используется алгоритм .

Псевдопростые числа генерируются с помощью хеш-функции и для проверки на простоту используется вероятностный тест Миллера — Рабина . К нему может добавляться одиночный тест простоты Люка .

Необходимое число итераций зависит от длины используемых чисел и от алгоритма проверки :

параметры	только М-Р тест	М-Р тест + тест Люка
p: 1024 бит q: 160 бит вероятность ошибки $2^{-80}$ $2^{-80}$	40	р: 3 q: 19
p: 2048 бит q: 224 бит вероятность ошибки $2^{-112}$ $2^{-112}$	56	р: 3 q: 24
p: 2048 бит q: 256 бит вероятность ошибки $2^{-112}$ $2^{-112}$	56	р: 3 q: 27
p: 3072 бит q: 256 бит вероятность ошибки $2^{-128}$ $2^{-128}$	64	р: 2 q: 27

Генерация случайных чисел

Для работы алгоритма требуется также генератор случайных или псевдослучайных чисел. Этот генератор нужен для создания частного пользовательского ключа x , а также для создания секретного случайного параметра $k$ $k$ .

Cтандарт предлагает различные способы генерации псевдослучайных чисел используя блочные шифры или хеш-функции.

Примечания

↑ .
↑ .
.
.
↑ .
↑ .
.
.
.
.
.
C. P. Schnorr. (англ.) // Advances in Cryptology — CRYPTO’ 89 Proceedings / Gilles Brassard. — New York, NY: Springer, 1990. — P. 239–252 . — ISBN 978-0-387-34805-6 . — doi : . 12 апреля 2022 года.
↑ .
.
.
.
.
.
.
.

Литература

Стандарты и патенты

FIPS. (англ.) .
FIPS. (англ.) .
FIPS. (англ.) .
FIPS. (англ.) .
FIPS. (англ.) . 26 ноября 2016 года.
FIPS. (англ.) .
FIPS. (англ.) .
David W. Kravitz. (англ.) .
NIST Special Publication 800-57 Part 1Revision 4. (англ.) .
(рус.) .
(англ.) .

Статьи

Marc Stevens, Pierre Karpman, Thomas Peyrin. (англ.) .
(англ.) .
J. Shawe-Taylor. (англ.) .
Xiaoyun Wang, Yiqun Lisa, Hongbo Yu. (англ.) .
Phong Q. Nguyen, Igor E. Shparlinski. (англ.) .
David Pointcheval, Jacques Stern. (англ.) .
Markus Schmid. (англ.) .
Don Johnson, Alfred Menezes, Scott Vanstone. (англ.) .
Elgamal T. (англ.) // / — IEEE , 1985. — P. 10—18. — ISSN ; — ;
Joppe W. Bos, J. Alex Halderman, Nadia Heninger, Jonathan Moore, Michael Naehrig, Eric Wustrow. (англ.) .