Давление детонации
- 1 year ago
- 0
- 0

Гидростатическое давление — давление столба жидкости над условным уровнем.
Благодаря полной удобоподвижности своих частиц капельные и газообразные жидкости, находясь в покое, передают давление одинаково во все стороны; давление это действует на всякую часть плоскости, ограничивающей жидкость, с силой Р , пропорциональной величине w этой поверхности, и направленной по нормали к ней. Отношение P/w , то есть давление р на поверхность, равную единице, называется гидростатическим давлением .
Простое уравнение P = pw может действительно служить для точного вычисления давления на данную поверхность сосуда, газов и капельных жидкостей, находящихся при таких условиях, что часть давления, зависящая от собственного веса жидкостей, ничтожно мала по сравнению с давлением, передаваемым им извне. Сюда относятся почти все случаи давлений газов и расчеты давлений воды в гидравлических прессах и аккумуляторах .
В каждой жидкости существует давление, обусловленное её собственным весом ; так как , то ; учтём, что и получим формулу .
Плотность жидкости зависит от температуры тела. Для очень точных вычислений плотность следует рассчитывать по специальной формуле. Давление на данной глубине одинаково во всех направлениях. Суммарное давление, обусловленное весом столба жидкости и давлением поршня, называют гидростатическим давлением .
Для бытовых расчетов можно принять, что с ростом глубины на каждые 10 метров пресной воды, давление увеличивается на 0,1 МПа (1 атмосфера ).
Это основное свойство жидкостей было открыто и проверено на опыте Блезом Паскалем в 1653 году.
Единицей измерения давления в международной системе единиц является паскаль . На практике гидростатическое давление часто измеряют в атмосферах , принимая за 1 атмосферу давление в 76 см ртутного столба, при температуре 0 °C при нормальном ускорении свободного падения 9,80665 м/с² .
На основании гидростатического парадокса можно гидростатическое давление измерять также высотой столба ртути или воды, способного производить то же давление на единицу поверхности.

Вычисление немного усложняется, когда надо узнать давление, производимое на не горизонтальную часть стенки сосуда вследствие тяжести налитой на него жидкости. Здесь причиной давления становится вес столбов жидкости, имеющих основанием каждую бесконечно малую частицу рассматриваемой поверхности, а высотой вертикальное расстояние от каждой такой частицы до свободной поверхности жидкости. Расстояния эти будут постоянны только для горизонтальных частей стенок и для бесконечно узких горизонтальных полосок, взятых на боковых стенках; к ним одним можно прилагать непосредственно формулу гидростатического давления. Для боковых же стенок надо суммировать, по правилам интегрального исчисления , давления на все горизонтальные элементы их поверхности; в результате получается общее правило: давление тяжелой жидкости на всякую плоскую стенку равняется весу столба этой жидкости, имеющему основанием площадь этой стенки, а высотой вертикальное расстояние её центра тяжести от свободной поверхности жидкости. Поэтому давление на дно сосуда будет зависеть только от величины поверхности этого дна, от высоты уровня жидкости в него налитой и от её плотности, от формы же сосуда оно зависеть не будет. Это положение известно под именем «гидростатического парадокса» и было разъяснено ещё Паскалем.
Действительно, оно кажется на первый взгляд неверным, потому что в сосудах с равными доньями, наполненными до равной высоты одной и той же жидкостью, вес её будет очень различный, если формы различны. Но вычисление и опыт (сделанный в первый раз Паскалем) показывают, что в сосуде, расширяющемся кверху, вес излишка жидкости поддерживается боковыми стенками и передается весам через их посредство, не действуя на дно, а в сосуде, суживающемся кверху, гидростатическое давление на боковые стенки действует снизу вверх и облегчает весы ровно на столько, сколько весило бы недостающее количество жидкости.
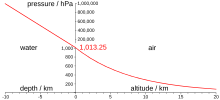
Гидростатическое давление жидкости с постоянной плотностью в однородном поле тяжести (= несжимаемая жидкость ) подчиняется закону Паскаля :
где:
⇒ = гидростатическое давление (p) зависит от высоты (h) жидкости .