Статистическая физика
Термодинамика Молекулярно-кинетическая теория
Статистики Максвелла-Больцмана Бозе-Эйнштейна Энионная статистика
Ансамбли Микроканонический Канонический Большой канонический Изотермо-изобарический
Термодинамика Уравнение состояния Цикл Карно Закон Дюлонга — Пти
Модели Модель Дебая Эйнштейна Модель Изинга
Потенциалы Внутренняя энергия Энтальпия Свободная энергия Гельмгольца потенциал Гиббса Большой термодинамический потенциал
См. также: Портал:Физика

Статистика Фе́рми — Дира́ка — квантовая статистика, применяемая к системам тождественных фермионов (частиц с полуцелым спином , подчиняющихся принципу Паули : одно квантовое состояние не может быть занято более чем одной частицей). Определяет вероятность , с которой данный энергетический уровень системы, находящейся в термодинамическом равновесии, оказывается занятым фермионом .

В статистике Ферми — Дирака среднее число частиц ${\displaystyle n_{i}}$ с энергией ${\displaystyle \varepsilon _{i}}$ есть

${\displaystyle n_{i}={\frac {g_{i}}{\exp \left({\dfrac {\varepsilon _{i}-\mu }{kT}}\right)+1}}}$ ,

где ${\displaystyle g_{i}}$ — кратность вырождения (число состояний частицы с энергией ${\displaystyle \varepsilon _{i}}$ ), ${\displaystyle \mu }$ — химический потенциал (при нуле температуры равен энергии Ферми ${\displaystyle E_{F}}$ ), ${\displaystyle k}$ — постоянная Больцмана , ${\displaystyle T}$ — абсолютная температура .

В идеальном ферми-газе при низких температурах ${\displaystyle \mu =E_{F}}$ . В этом случае, если ${\displaystyle g_{i}=1}$ , функция числа (доли) заполнения уровней частицами называется функцией Ферми :

${\displaystyle F(\varepsilon ,T)={\frac {1}{\exp \left({\dfrac {\varepsilon -E_{F}}{kT}}\right)+1}}.}$

Указанная статистика предложена в 1926 году итальянским физиком Энрико Ферми и одновременно английским физиком Полем Дираком , который выяснил её квантово-механический смысл. В 1927 статистика была применена Арнольдом Зоммерфельдом к электронам в металле .

Свойства статистики Ферми — Дирака

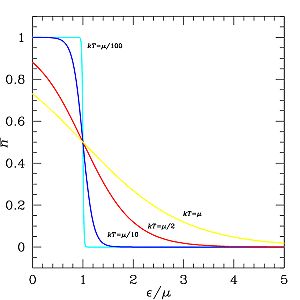
Функция Ферми — Дирака обладает следующими свойствами:

• безразмерна;
• принимает вещественные значения в диапазоне от 0 до 1;
• убывает с энергией, резко спадая вблизи энергии, равной химическому потенциалу;
• при абсолютном нуле имеет вид ступеньки со скачком от 1 до 0 при ${\displaystyle \varepsilon =\mu }$ , а при подъёме температуры скачок заменяется всё более плавным спадом;
• при ${\displaystyle \varepsilon =\mu }$ всегда ${\displaystyle F=1/2}$ независимо от температуры.

Математический и физический смысл

Функцией Ферми — Дирака ${\displaystyle F(\varepsilon ,T)}$ задаются числа заполнения ( англ. occupancy factor) квантовых состояний. Хотя она нередко называется «распределением», с точки зрения аппарата теории вероятностей она не является ни функцией распределения , ни плотностью распределения . В отношении этой функции, скажем, не может ставиться вопрос о нормировке .

Давая информацию о проценте заполненности состояний, функция ${\displaystyle F(\varepsilon ,T)}$ ничего не говорит о наличии этих состояний. Для систем с дискретными энергиями набор их возможных значений задаётся перечнем ${\displaystyle \varepsilon _{1}}$ , ${\displaystyle \varepsilon _{2}}$ и т.д., а для систем с непрерывным спектром энергий состояния характеризуются « плотностью состояний » ${\displaystyle \rho (\varepsilon)}$ (Дж ^-1 или Дж ^-1 м ^-3 ). Функция

${\displaystyle f(\varepsilon)=\left(\int \rho (\varepsilon)F(\varepsilon)d\varepsilon \right)^{-1}\rho (\varepsilon)F(\varepsilon)}$

является плотностью распределения (Дж ^-1 ) частиц по энергии и нормирована. Для краткости, аргумент ${\displaystyle T}$ опущен. В наиболее традиционных случаях ${\displaystyle \rho (\varepsilon)\sim {\sqrt {\varepsilon }}}$ .

Классический (максвелловский) предел

При высоких температурах и/или низких концентрациях частиц статистика Ферми — Дирака (равно как и статистика Бозе — Эйнштейна ) переходят в статистику Максвелла — Больцмана . А именно, в таких условиях

${\displaystyle F(\varepsilon)=\exp \left({\frac {E_{F}-\varepsilon }{kT}}\right)}$ .

После подстановки плотности состояний ${\displaystyle \rho (\varepsilon)}$ и интегрирования по ${\displaystyle \varepsilon }$ от 0 до ${\displaystyle +\infty }$ выражение для ${\displaystyle f}$ примет вид

${\displaystyle f(\varepsilon)={\frac {2\pi {\sqrt {\varepsilon }}}{\sqrt {(\pi kT)^{3}}}}\exp \left(-{\frac {\varepsilon }{kT}}\right)}$ .

Это и есть плотность распределения Максвелла (по энергиям).

Распределением Максвелла (особенно хорошо работающим применительно к газам) описываются классические «различимые» частицы. Другими словами, конфигурации «частица ${\displaystyle A}$ в состоянии 1 и частица ${\displaystyle B}$ в состоянии 2» и «частица ${\displaystyle B}$ в состоянии 1 и частица ${\displaystyle A}$ в состоянии 2» считаются разными.

Применение статистики Ферми — Дирака

Характеристика сферы применения

Статистики Ферми — Дирака, а также Бозе — Эйнштейна применяются в тех случаях, когда необходимо учитывать квантовые эффекты и «неразличимость» частиц. В парадигме различимости оказалось, что распределение частиц по энергетическим состояниям приводит к нефизическим результатам для энтропии , что известно как парадокс Гиббса . Эта проблема исчезла, когда стал ясен тот факт, что все частицы неразличимы.

Статистика Ферми — Дирака относится к фермионам (частицы, на которые действует принцип Паули), а статистика Бозе — Эйнштейна — к бозонам . Квантовые эффекты проявляются тогда, когда концентрация частиц ${\displaystyle N/V\geqslant n_{q}}$ (где ${\displaystyle N}$ — число частиц, ${\displaystyle V}$ — объём, ${\displaystyle n_{q}}$ — квантовая концентрация). Квантовой называется концентрация, при которой расстояние между частицами соразмерно с длиной волны де Бройля , то есть волновые функции частиц соприкасаются, но не перекрываются. Квантовая концентрация зависит от температуры.

Конкретные примеры

Статистика Ферми — Дирака часто используется для описания поведения ансамбля электронов в твёрдых телах; на ней базируются многие положения теории полупроводников и электроники в целом. Например, концентрация электронов ( дырок ) в зоне проводимости ( валентной зоне ) полупроводника в равновесии рассчитывается как

${\displaystyle n=\int \limits _{E_{c}}^{+\infty }\rho (\varepsilon)F(\varepsilon)\,d\varepsilon ,\quad p=\int \limits _{-\infty }^{E_{v}}\rho (\varepsilon)(1-F(\varepsilon))\,d\varepsilon }$ ,

где ${\displaystyle E_{c}}$ ( ${\displaystyle E_{v}}$ ) — энергия дна зоны проводимости ( потолка валентной зоны ). Формула для туннельного тока между двумя областями, разделёнными квантовым потенциальным барьером , имеет общий вид

${\displaystyle j={\mbox{const}}\cdot \int \Theta (\varepsilon)\left[F_{L}(\varepsilon)-F_{R}(\varepsilon)\right]\,d\varepsilon }$ ,

где ${\displaystyle \Theta }$ — коэффициент прозрачности барьера, а ${\displaystyle F_{L}}$ , ${\displaystyle F_{R}}$ — функции Ферми — Дирака в областях слева и справа от барьера.

Вывод распределения Ферми — Дирака

Рассмотрим состояние частицы в системе, состоящей из множества частиц. Пусть энергия такой частицы равна ${\displaystyle \varepsilon }$ . Например, если наша система — это некий квантовый газ в «ящике», то подобное состояние может описываться частной волновой функцией. Известно, что для большого канонического ансамбля , функция распределения имеет вид

${\displaystyle Z=\sum _{s}e^{-(E(s)-\mu N(s))/kT},}$

где ${\displaystyle E(s)}$ — энергия состояния ${\displaystyle s}$ , ${\displaystyle N(s)}$ — число частиц, находящихся в состоянии ${\displaystyle s}$ , ${\displaystyle \mu }$ — химический потенциал , ${\displaystyle s}$ — индекс, пробегающий все возможные микросостояния системы.

В данном контексте система имеет фиксированные состояния. Если какое либо состояние занято ${\displaystyle n}$ частицами, то энергия системы — ${\displaystyle n\cdot \varepsilon }$ . Если состояние свободно, энергия имеет значение 0 . Будем рассматривать равновесные одночастичные состояния как резервуар . После того, как система и резервуар займут одно и то же физическое пространство, начинает происходить обмен частицами между двумя состояниями (фактически, это явление мы и исследуем). Отсюда становится ясно, почему используется описанная выше функция распределения, которая, через химический потенциал, учитывает поток частиц между системой и резервуаром.

Для фермионов , каждое состояние может быть либо занято одной частицей, либо свободно. Поэтому, наша система имеет два множества: занятых (разумеется, одной частицей) и незанятых состояний, обозначающихся ${\displaystyle s_{1}}$ и ${\displaystyle s_{2}}$ соответственно. Видно, что ${\displaystyle E(s_{1})=\varepsilon }$ , ${\displaystyle N(s_{1})=1}$ , и ${\displaystyle E(s_{2})=0}$ , ${\displaystyle N(s_{2})=0}$ . Поэтому функция распределения принимает вид:

${\displaystyle Z=\sum _{i=1}^{2}e^{-(E(s_{i})-\mu N(s_{i}))/kT}=e^{-(\varepsilon -\mu)/kT}+1.}$

Для большого канонического ансамбля, вероятность того, что система находится в микросостоянии ${\displaystyle s_{\alpha }}$ вычисляется по формуле

${\displaystyle P(s_{\alpha })={\frac {e^{-(E(s_{\alpha })-\mu N(s_{\alpha }))/kT}}{Z}}.}$

Наличие состояния, занятого частицей, означает, что система находится в микросостоянии ${\displaystyle s_{1}}$ , вероятность которого

${\displaystyle {\bar {n}}=P(s_{1})={\frac {e^{-(E(s_{1})-\mu N(s_{1}))/kT}}{Z}}={\frac {e^{-(\varepsilon -\mu)/kT}}{e^{-(\varepsilon -\mu)/kT}+1}}={\frac {1}{e^{(\varepsilon -\mu)/kT}+1}}.}$

${\displaystyle {\bar {n}}}$ называется распределением Ферми — Дирака . Для фиксированной температуры ${\displaystyle T}$ , ${\displaystyle {\bar {n}}(\varepsilon)}$ есть вероятность того, что состояние с энергией ${\displaystyle \varepsilon }$ будет занято фермионом.

Учтём, что энергетический уровень ${\displaystyle \varepsilon }$ имеет вырождение ${\displaystyle g_{\varepsilon }}$ . Теперь можно произвести простую модификацию:

${\displaystyle {\bar {n}}=g_{\varepsilon }\cdot {\frac {1}{e^{(\varepsilon -\mu)/kT}+1}}.}$

Здесь ${\displaystyle {\bar {n}}={\bar {n}}(\varepsilon)}$ — ожидаемая доля частиц во всех состояниях с энергией ${\displaystyle \varepsilon }$ .

Уточнение влияния температуры

Для систем, имеющих температуру ${\displaystyle T}$ ниже ${\displaystyle T_{F}=E_{F}/k}$ , а иногда (не вполне правомерно) и для более высоких температур используется аппроксимация ${\displaystyle \mu \approx E_{F}}$ . Но в общем случае химический потенциал зависит от температуры — и в ряде задач эту зависимость целесообразно учитывать. Функция ${\displaystyle \mu }$ представляется с любой точностью степенным рядом по чётным степеням отношения ${\displaystyle T/T_{F}<1}$ :

${\displaystyle \mu =E_{F}\sum _{n=0,1,2\dots }{\left[(-1)^{n}{\frac {\pi ^{2n}}{2^{2n}(2n+1)}}\left({\frac {kT}{E_{F}}}\right)^{2n}\right]}=E_{F}\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {kT}{E_{F}}}\right)^{2}+{\frac {\pi ^{4}}{80}}\left({\frac {kT}{E_{F}}}\right)^{4}+\ldots \right]}$ .

См. также