Interested Article - Комплексное число
- 2021-03-15
- 1
Ко́мпле́ксные чи́сла (от лат. complexus — связь, сочетание ; о двойном ударении см. примечание ) — числа вида где — вещественные числа , — мнимая единица , то есть число, для которого выполняется равенство: Множество комплексных чисел обычно обозначается символом Вещественные числа можно рассматривать как частный случай комплексных, они имеют вид Главное свойство — в нём выполняется основная теорема алгебры , то есть любой многочлен -й степени ( ) имеет корней . Доказано , что система комплексных чисел логически непротиворечива .
Так же как и для вещественных чисел, для комплексных чисел определены операции сложения , вычитания , умножения и деления . Однако многие свойства комплексных чисел отличаются от свойств вещественных чисел; например, нельзя указать, какое из двух комплексных чисел больше или меньше . Удобно представлять комплексные числа точками на комплексной плоскости ; например, для изображения сопряжённых чисел используется операция отражения относительно горизонтальной оси . Альтернативное представление комплексного числа в тригонометрической записи оказалось полезным для вычисления степеней и корней . Функции комплексного аргумента изучаются в комплексном анализе .
Первоначально идея о необходимости использования комплексных чисел возникла в результате формального решения кубических уравнений , при котором в формуле Кардано под знаком квадратного корня получалось отрицательное число . Большой вклад в исследование комплексных чисел внесли такие математики как Эйлер , который ввёл общепризнанное обозначение для мнимой единицы, Декарт , Гаусс . Сам термин «комплексное число» ввёл в науку Гаусс в 1831 году .
Уникальные свойства комплексных чисел и функций нашли широкое применение для решения многих практических задач в различных областях математики, физики и техники: в обработке сигналов , теории управления , электромагнетизме , теории колебаний , теории упругости и многих других . Преобразования комплексной плоскости оказались полезны в картографии и гидродинамике . Современная физика полагается на описание мира с помощью квантовой механики , которая опирается на систему комплексных чисел.
Известно также несколько обобщений комплексных чисел — например, кватернионы .
Комплексная арифметика
Связанные определения
Всякое комплексное число состоит из двух компонентов :
-
Величина
называется
вещественной частью
числа
и согласно международным стандартам
ISO 31-11
и
ISO 80000-2
обозначается
или
В источниках иногда встречается
готический
символ
:
- Если , то называется чисто мнимым числом . Вместо обычно пишут просто В некоторых источниках такие числа называются просто мнимыми , однако в других источниках мнимыми могут называться любые комплексные числа у которых Поэтому термин мнимое число неоднозначен, и использовать его без дополнительных разъяснений не рекомендуется.
-
Величина
называется
мнимой частью
числа
и согласно международным стандартам
ISO 31-11
и
ISO 80000-2
обозначается
или
В источниках иногда встречается готический символ
:
- Если , то является вещественным числом . Вместо обычно пишут просто Например, комплексный ноль обозначается просто как
Противоположным для комплексного числа является число Например, для числа противоположным будет число
В отличие от вещественных, комплексные числа нельзя сравнивать на больше/меньше ; доказано, что нет способа распространить порядок, заданный для вещественных чисел, на все комплексные так, чтобы порядок был согласован с арифметическими операциями (чтобы из вытекало , а из и вытекало ). Однако, комплексные числа можно сравнивать на равно/не равно :
- означает, что и (два комплексных числа равны между собой тогда и только тогда , когда равны их вещественные и мнимые части).
Четыре арифметические операции для комплексных чисел (определённые ниже) имеют те же свойства, что и аналогичные операции с вещественными числами .
Сложение и вычитание
Определение сложения и вычитания комплексных чисел :
Следующая таблица показывает основные свойства сложения для любых комплексных
| Свойство | Алгебраическая запись |
|---|---|
| Коммутативность ( переместительность ) | |
| Ассоциативность ( сочетательность ) | |
| Свойство нуля | |
| Свойство противоположного элемента | |
| Выполнение вычитания через сложение |
Умножение
Определение произведения комплексных чисел и
Следующая таблица показывает основные свойства умножения для любых комплексных
| Свойство | Алгебраическая запись |
|---|---|
| Коммутативность ( переместительность ) | |
| Ассоциативность ( сочетательность ) | |
| Свойство единицы | |
| Свойство нуля | |
| Дистрибутивность (распределительность) умножения относительно сложения |
Правила для степеней мнимой единицы:
- и т. д.
То есть для любого целого числа верна формула , где выражение означает получение остатка от деления на 4.
После определения операций с комплексными числами выражение можно воспринимать не как формальную запись, а как выражение, составленное по приведённым выше правилам сложения и умножения. Чтобы это показать, раскроем все входящие в него переменные, следуя и определению сложения и умножения:
Деление
Комплексное число называется сопряжённым к комплексному числу (подробнее ).
Для каждого комплексного числа кроме нуля, можно найти обратное к нему комплексное число Для этого умножим числитель и знаменатель дроби на число комплексно сопряжённое знаменателю
Определим результат деления комплексного числа на ненулевое число
Как и для вещественных чисел, деление можно заменить умножением делимого на число, обратное к делителю .
Другие операции
Для комплексных чисел определены также извлечение корня , возведение в степень и логарифмирование .
Основные отличия комплексных чисел от вещественных
Уже упоминалось, что комплексные числа нельзя сравнивать на больше-меньше (иными словами, на множестве комплексных чисел не задано отношение порядка ). Другое отличие: любой многочлен степени с комплексными (в частности, вещественными) коэффициентами имеет, с учётом кратности , ровно комплексных корней ( основная теорема алгебры ) .
В системе вещественных чисел из отрицательного числа нельзя извлечь корень чётной степени. Для комплексных чисел возможно извлечение корня из любого числа любой степени, однако результат неоднозначен — комплексный корень -й степени из ненулевого числа имеет различных комплексных значений . См., например, корни из единицы .
Дополнительные отличия имеют функции комплексного переменного .
Замечания
Число не является единственным числом, квадрат которого равен Число также обладает этим свойством.
Выражение ранее часто использовавшееся вместо в современных учебниках считается некорректным, и под знаком радикала стали допускаться только неотрицательные выражения (см. « Арифметический корень »). Во избежание ошибок, выражение с квадратными корнями из отрицательных величин в настоящее время принято записывать как а не несмотря на то, что даже в XIX веке второй вариант записи считался допустимым .
Пример возможной ошибки при неосторожном использовании устаревшей записи:
Эта ошибка связана с тем, что квадратный корень из определён неоднозначно (см. ниже ). При использовании современной записи такой ошибки не возникло бы :
Геометрическое представление
Комплексная плоскость
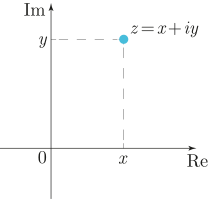
Комплексные числа можно представить на плоскости с прямоугольной системой координат : числу соответствует точка плоскости с координатами (а также радиус-вектор , соединяющий начало координат с этой точкой). Такая плоскость называется комплексной . Вещественные числа на ней расположены на горизонтальной оси, мнимая единица изображается единицей на вертикальной оси; по этой причине горизонтальная и вертикальная оси называются соответственно вещественной и мнимой осями .
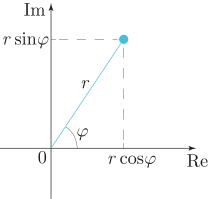
Бывает удобно рассматривать на комплексной плоскости также полярную систему координат (см. рисунок справа), в которой координатами точки являются расстояние до начала координат ( модуль ) и угол радиус-вектора точки с горизонтальной осью ( аргумент ).
В этом представлении сумма комплексных чисел соответствует векторной сумме соответствующих радиус-векторов, а вычитанию чисел соответствует вычитание радиус-векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются (последнее несложно вывести из формулы Эйлера или из тригонометрических формул суммы ). Если модуль второго сомножителя равен 1, то умножение на него соответствует повороту радиус-вектора первого числа на угол, равный аргументу второго числа . Этот факт объясняет широкое использование комплексного представления в теории колебаний , где вместо терминов «модуль» и «аргумент» используются термины « амплитуда » и « фаза » .
Пример : умножение на поворачивает радиус-вектор числа на прямой угол в положительном направлении, а после умножения на радиус-вектор поворачивается на прямой угол в отрицательном направлении.
Модуль
Модулем ( абсолютной величиной ) комплексного числа называется длина радиус-вектора соответствующей точки комплексной плоскости (или, что то же самое, расстояние от точки комплексной плоскости до начала координат). Модуль комплексного числа обозначается (иногда или ) и определяется выражением
Если является вещественным числом , то совпадает с абсолютной величиной этого числа в вещественном понимании термина.
Для любых комплексных имеют место следующие свойства модуля :
- 1) , причём только при
- 2) ( неравенство треугольника );
- 3)
- 4)
- 5) для пары комплексных чисел и модуль их разности равен расстоянию между соответствующими точками комплексной плоскости;
-
6) модуль числа
связан с вещественной и мнимой частями этого числа соотношениями:
Аргумент
Аргументом ненулевого комплексного числа называется угол между радиус-вектором соответствующей точки и положительной вещественной полуосью. Аргумент числа измеряется в радианах и обозначается . Из этого определения следует, что
Для комплексного нуля значение аргумента не определено, для ненулевого числа аргумент определяется с точностью до , где — любое целое число. Главным значением аргумента называется такое значение , что Главное значение может обозначаться .
Некоторые свойства аргумента :
-
1) аргумент обратного числа отличается знаком от аргумента исходного:
-
2) аргумент произведения равен сумме аргументов сомножителей:
-
3) аргумент частного от деления равен разности аргументов делимого и делителя:
Сопряжённые числа
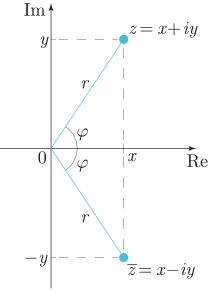
Если комплексное число равно то число называется сопряжённым (или комплексно-сопряжённым) к (обозначается также ). На комплексной плоскости сопряжённые числа получаются друг из друга зеркальным отражением относительно вещественной оси. Модуль сопряжённого числа такой же, как исходного, а их аргументы различаются знаком :
Переход к сопряжённому числу можно рассматривать как одноместную операцию , которая сохраняет все арифметические и алгебраические свойства. Эта операция имеет следующие свойства :
- тогда и только тогда, когда — вещественное число.
- (сопряжённое к сопряжённому есть исходное; иначе говоря, операция сопряжения является инволюцией ).
Произведение комплексно-сопряжённых чисел — неотрицательное вещественное число, равное нулю только для нулевого z :
Сумма комплексно-сопряжённых чисел — вещественное число :
Другие соотношения :
Или, в общем виде: где — произвольный многочлен с вещественными коэффициентами. В частности, если комплексное число является корнем многочлена с вещественными коэффициентами, то сопряжённое число тоже является его корнем. Из этого следует, что существенно комплексные корни такого многочлена (то есть корни, не являющиеся вещественными) разбиваются на комплексно-сопряжённые пары .
Пример
Тот факт, что произведение есть вещественное число, можно использовать, чтобы выразить комплексную дробь в канонической форме, то есть избавиться от мнимости в знаменателе. Для этого надо умножить числитель и знаменатель на сопряжённое к знаменателю выражение , например:
Формы представления комплексного числа
Алгебраическая форма
Выше использовалась запись комплексного числа в виде такая запись называется алгебраической формой комплексного числа. Две другие основные формы записи связаны с представлением комплексного числа в полярной системе координат .
Тригонометрическая форма
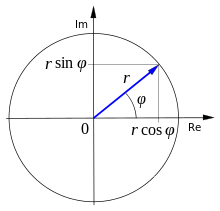
Если вещественную и мнимую части комплексного числа выразить через модуль и аргумент (то есть , ), то всякое комплексное число , кроме нуля, можно записать в тригонометрической форме :
Как уже сказано выше, для нуля аргумент не определён; для ненулевого числа определяется с точностью до целого кратного
Показательная форма
Фундаментальное значение в комплексном анализе имеет формула Эйлера :
где — число Эйлера , , — косинус и синус , — комплексная экспонента , продолжающая вещественную на случай общего комплексного показателя степени.
Применяя эту формулу к тригонометрической форме, получим показательную форму комплексного числа :
Следствия
- (1) Модуль выражения где число вещественно, равен 1.
- (2) — при существенно комплексном аргументе эти равенства могут служить определением (комплексного) косинуса и синуса .
Пример . Представим в тригонометрической и показательной форме число
- (поскольку находится в III координатной четверти).
Отсюда:
Формула Муавра и извлечение корней
Эта формула помогает возводить в целую степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид :
где — модуль, а — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году. Приведённая формула справедлива при любом целом , не обязательно положительном.
Аналогичная формула применима также и при вычислении корней -й степени из ненулевого комплексного числа :
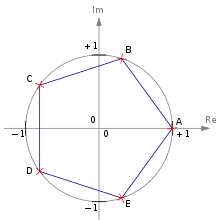
где k принимает все целые значения от до . Это значит, что корни -й степени из ненулевого комплексного числа существуют для любого натурального и их количество равно . На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного -угольника , вписанного в окружность радиуса с центром в начале координат (см. рисунок).
Главное значение корня
Если в формуле Муавра в качестве аргумента выбрано его главное значение, то значение корня при называется главным значением корня . Например, главное значение числа равно
Квадратный корень
Для извлечения квадратного корня из комплексного числа можно преобразовать это число в тригонометрическую форму и воспользоваться формулой Муавра для Но существует и чисто алгебраическое представление для двух значений корня. При корнями из числа является пара чисел: где :
Здесь — функция «знак» , а радикалы обозначают обычный арифметический корень из неотрицательного вещественного числа. Формула легко проверяется возведением в квадрат. Число является главным значением квадратного корня.
Пример : для квадратного корня из формулы дают два значения:
История
Зарождение понятия комплексного числа исторически было связано с желанием «легализовать» квадратные корни из отрицательных чисел. Как постепенно выяснилось, комплексные числа обладают богатыми алгебраическими и аналитическими свойствами; в частности, извлечение корней из них всегда возможно, хотя и неоднозначно.
Впервые, по-видимому, мнимые величины были упомянуты в труде Кардано «Великое искусство, или об алгебраических правилах» (1545), в рамках формального решения задачи по вычислению двух чисел, сумма которых равна 10, а произведение равно 40. Он получил для этой задачи квадратное уравнение, корни которого: и В комментарии к решению он написал: «эти сложнейшие величины бесполезны, хотя и весьма хитроумны», и «арифметические соображения становятся всё более неуловимыми, достигая предела столь же утончённого, сколь и бесполезного» .
Возможность использования мнимых величин при решении кубического уравнения впервые описал Бомбелли (1572), он же дал правила сложения, вычитания, умножения и деления комплексных чисел. Уравнение имеет вещественный корень однако по формулам Кардано получаем: Бомбелли обнаружил, что так что сумма этих величин даёт нужный вещественный корень. Он отметил, что в подобных ( неприводимых ) случаях комплексные корни уравнения всегда сопряжены, поэтому в сумме и получается вещественное значение. Разъяснения Бомбелли положили начало успешному применению в математике комплексных чисел .
Выражения, представимые в виде появляющиеся при решении квадратных и кубических уравнений, где стали называть «мнимыми» в XVI—XVII веках с подачи Декарта , который называл их так, отвергая их реальность. Для многих других крупных учёных XVII века природа и право на существование мнимых величин тоже представлялись весьма сомнительными. Лейбниц , например, в 1702 году писал: «Дух божий нашёл тончайшую отдушину в этом чуде анализа, уроде из мира идей, двойственной сущности, находящейся между бытием и небытием, которую мы называем мнимым корнем из отрицательной единицы». Несмотря на эти сомнения, математики уверенно применяли к «мнимым» числам привычные для вещественных величин алгебраические правила и получали корректные результаты .
Долгое время было неясно, все ли операции над комплексными числами приводят к комплексным результатам или же, например, извлечение корня может привести к открытию ещё какого-то нового типа чисел. Задача о выражении корней степени из данного числа была решена в работах Муавра (1707) и Котса (1722) .
Символ для обозначения мнимой единицы предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву латинского слова imaginarius — «мнимый». Он же распространил все стандартные функции, включая логарифм , на комплексную область. Эйлер также высказал в 1751 году мысль, что в системе комплексных чисел любой многочлен имеет корень ( основная теорема алгебры , до Эйлера сходные предположения высказывали Альбер Жирар и Рене Декарт ) . К такому же выводу пришёл д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит Гауссу (1799) . Гаусс и ввёл в широкое употребление термин «комплексное число» в 1831 году (ранее термин использовал в том же смысле французский математик Лазар Карно в 1803 году, но тогда он не получил распространения) .
Геометрическое представление комплексных чисел, немало способствовавшее их легализации, предложили в конце XVIII — начале XIX веков сначала Вессель и Арган (их работы не привлекли внимания), а затем Гаусс . Арифметическая (стандартная) модель комплексных чисел как пар вещественных чисел была построена Гамильтоном («Теория алгебраических пар», 1837); это доказало непротиворечивость их свойств. Термины «модуль», «аргумент» и «сопряжённое число» ввёл в начале XIX века Коши , значительно продвинувший комплексный анализ . С XIX века началось бурное и чрезвычайно плодотворное развитие исследований функций комплексного переменного .
С учётом этого успешного подхода начались поиски способа представления векторов в трёхмерном пространстве , аналогичное комплексной плоскости. В результате пятнадцатилетних поисков Гамильтон предложил в 1843 году обобщение комплексных чисел — кватернионы , которые он был вынужден сделать не трёхмерными, а четырёхмерными (трёхмерные векторы изображала мнимая часть кватернионов); также Гамильтону пришлось отказаться от коммутативности операции умножения .
В 1893 году Чарлз Штейнмец предложил использовать комплексные числа для расчётов электрических цепей переменного тока (см. ).
Комплексные функции
Аналитические функции
Комплексная функция одной переменной — это функция , которая определена на некоторой области комплексной плоскости и ставит в соответствие точкам этой области комплексные значения . Примеры:
Каждая комплексная функция может рассматриваться как пара вещественных функций от двух переменных: определяющих её вещественную и мнимую часть соответственно. Функции , называются компонентами комплексной функции Аналогично определяется функция нескольких комплексных переменных .
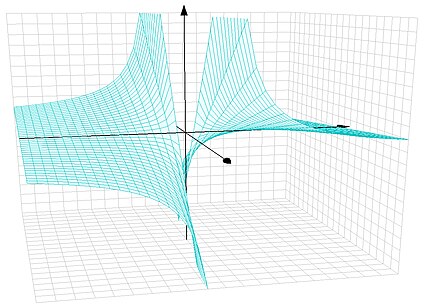
Наглядное представление комплексной функции графиком затруднительно, так как даже для функции одной комплексной переменной график требует четырёх измерений (два на область определения и ещё два для области значений). Если вместо значения функции рассматривать её модуль то полученный рельеф функции размещается в трёх измерениях и даёт некоторое представление о поведении функции .
Все стандартные функции анализа — многочлен , дробно-линейная функция , степенная функция , экспонента , тригонометрические функции , обратные тригонометрические функции , логарифм — могут быть распространены на комплексную плоскость. При этом для них будут иметь место те же алгебраические, дифференциальные и другие тождества, что и для вещественного оригинала , например:
Для комплексных функций определяются понятия предела , непрерывности и производной так же, как в вещественном анализе, с заменой абсолютной величины на комплексный модуль .
Дифференцируемые комплексные функции (то есть функции, имеющие производную) обладают рядом особенностей по сравнению с вещественными .
- Вещественная и мнимая часть дифференцируемой функции — гармонические функции , связанные условиями Коши — Римана .
- Всякая дифференцируемая в некоторой окрестности точки комплексная функция дифференцируема неограниченное число раз в этой точке (то есть аналитична , или голоморфна ).
Определённый интеграл для функций одной комплексной переменной, вообще говоря, зависит от пути интегрирования (то есть выбора кривой от начальной до конечной точки в комплексной плоскости). Однако если интегрируемая функция аналитична в односвязной области , то её интеграл внутри этой области не зависит от пути .
Преобразования комплексной плоскости
Всякая комплексная функция может рассматриваться как преобразование комплексной плоскости (или как преобразование одной комплексной плоскости в другую). Примеры:
- — параллельный перенос , определяемый радиус-вектором точки
- где — комплексное число с единичным модулем, — это поворот вокруг начала координат на угол, равный аргументу
- — зеркальное отражение относительно вещественной оси.
Поскольку любое движение на плоскости есть комбинация перечисленных трёх преобразований, функции и дают общее выражение для движения на комплексной плоскости .
Другие линейные преобразования :
- , где — положительное вещественное число, задаёт растяжение с коэффициентом , если или сжатие в раз, если
- преобразования и где — произвольные комплексные числа, задают преобразование подобия ;
- преобразование где — общий вид аффинного преобразования комплексной плоскости (при преобразование не будет аффинным, так как оно будет вырождать плоскость в прямую).
Важную роль в комплексном анализе играют дробно-линейные преобразования :
При этом (иначе функция вырождается в константу). Характеристическое свойство дробно-линейного преобразования: оно переводит окружности и прямые в окружности и прямые (то есть в так называемые обобщённые окружности , в число которых входят «окружности бесконечного радиуса» — прямые). При этом образом окружности может оказаться прямая, и наоборот .
Среди других практически полезных функций преобразования: инверсия функция Жуковского . Инверсия, как и дробно-линейное преобразование, переводит обобщённые окружности в обобщённые окружности.
Аналитическая геометрия на комплексной плоскости
Исследование плоских фигур нередко облегчается, если перенести их на комплексную плоскость. Многие теоремы планиметрии допускают наглядную и компактную запись с помощью комплексных чисел, например :
- Три (различные) точки лежат на одной прямой тогда и только тогда, когда выполняется условие:
-
- является вещественным числом.
- Четыре (различные) точки лежат на одной обобщённой окружности (окружности или прямой) тогда и только тогда, когда выполняется условие:
-
- отношение является вещественным числом.
- Если даны три вершины параллелограмма : то четвёртая определяется равенством :
Параметрическое уравнение прямой на комплексной плоскости имеет вид :
- где — комплексные числа, — произвольный вещественный параметр.
Угол между двумя прямыми и равен В частности, прямые перпендикулярны , только когда — чисто мнимое число. Две прямые параллельны тогда и только тогда, когда есть вещественное число; если при этом также вещественно, то обе прямые совпадают. Каждая прямая рассекает комплексную плоскость на две полуплоскости: на одной из них выражение положительно, на другой — отрицательно .
Уравнение окружности с центром и радиусом имеет чрезвычайно простой вид: Неравенство описывает внутренность окружности ( открытый круг) . Часто удобна параметрическая форма уравнения окружности :
Место в общей алгебре, топологии и теории множеств
Множество комплексных чисел образует поле , которое является конечным расширением степени 2 поля вещественных чисел Основное алгебраическое свойство — оно алгебраически замкнуто , то есть в нём любой многочлен имеет (комплексные) корни и, следовательно, распадается на линейные множители. Говорят также, что есть алгебраическое замыкание поля
Характеристика комплексного поля равна нулю, мощность как множества та же, что и у поля вещественных чисел, то есть континуум . Теорема Фробениуса установила, что существуют только два тела , являющиеся конечными расширениями — поле комплексных чисел и тело кватернионов .
Превратить поле комплексных чисел в упорядоченное поле невозможно, потому что в упорядоченном поле квадрат любого элемента неотрицателен, и мнимая единица в нём не может существовать.
Из свойств модуля следует, что комплексные числа образуют структуру двумерного нормированного пространства над полем
Поле допускает бесконечно много автоморфизмов , но только один из них (не считая тождественного) оставляет вещественные числа на месте .
Поля и — единственные связные локально компактные топологические поля .
Некоторые практические применения
Те особенности комплексных чисел и функций, которые отличают их от вещественных, оказались полезными, а часто и незаменимыми в математике, в естественных науках и технике.
Математика
Приложения комплексных чисел сами по себе занимают видное место в математике — в частности, понятия алгебраических чисел , нахождение корней многочленов , теория Галуа , комплексный анализ и т. д.
Перенеся геометрическую задачу с обычной плоскости на комплексную, мы нередко получаем возможность значительно упростить её решение .
Многие сложные задачи теории чисел (например, теория биквадратичных вычетов ) и вещественного математического анализа (например, вычисление сложных или несобственных интегралов ) удалось решить только с помощью средств комплексного анализа . Мощным инструментом для открытий в теории чисел оказались, например, гауссовы числа вида где — целые числа . Для исследования распределения простых чисел понадобилась комплексная дзета-функция Римана .
Нередко проблемы вещественного анализа проясняются при их комплексном обобщении. Классический пример — разложение в ряд Тейлора
Этот ряд сходится только в интервале , хотя точки не являются какими-то особенными для приведённой функции. Положение проясняется при переходе к функции комплексного переменного у которой обнаруживаются две особые точки: полюса Соответственно, эту функцию можно разложить в ряд только в круге единичного радиуса .
При решении линейных дифференциальных уравнений важно сначала найти все комплексные корни характеристического многочлена, а затем попытаться решить систему в терминах базовых экспонент . В разностных уравнениях используются для аналогичной цели комплексные корни характеристического уравнения системы разностных уравнений . С помощью теории вычетов , являющейся частью комплексного анализа, вычисляются многие сложные интегралы по замкнутым контурам ..
Исследование функции часто связано с анализом её частотного спектра с помощью комплексного преобразования Фурье или Лапласа .
О представлении комплексных чисел в информатике и компьютерной поддержке комплексной арифметики изложено в статье Комплексный тип данных .
Конформное отображение
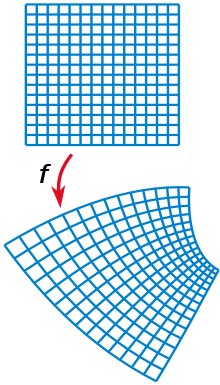
Как уже отмечалось выше, всякая комплексная функция может рассматриваться как преобразование одной комплексной плоскости в другую. Гладкая ( аналитическая ) функция обладает двумя особенностями: если в заданной точке производная не равна нулю, то коэффициент растяжения/сжатия при этом преобразовании одинаков по всем направлениям, угол поворота также постоянен ( конформное отображение ) . С этим фактом связано широкое применение комплексных функций в картографии и гидродинамике .
Квантовая механика
Основой квантовой механики является понятие комплексной волновой функции . Для описания динамики квантовой системы используются дифференциальные уравнения с комплексными коэффициентами типа уравнения Шрёдингера . Решения этих уравнений заданы в комплексном гильбертовом пространстве . Операторы, соответствующие наблюдаемым величинам, эрмитовы . Коммутатор операторов координаты и импульса представляет собой мнимое число:
Здесь — редуцированная постоянная Планка , то есть ( постоянная Дирака ) .
Важную роль в квантовой механике играют матрицы Паули и матрицы Дирака , некоторые из них содержат комплексные значения . Ю. Вигнер уточнял, что «…использование комплексных чисел в квантовой механике не является вычислительным трюком прикладной математики; они входят в самую суть формулировки основных законов квантовой механики» .
Электротехника
Поскольку переменный ток есть колебательный процесс, его удобно описывать и исследовать с применением комплексных чисел. Вводятся также понятия импеданса, или комплексного сопротивления , для реактивных элементов электрической цепи, таких как ёмкость и индуктивность, — это помогает рассчитать токи в цепи . Ввиду того, что традиционно символ в электротехнике обозначает величину тока, мнимую единицу там обозначают буквой . Во многих областях электротехники (в основном радиочастотной и оптической) используется не запись уравнений тока и напряжения для цепи, а напрямую уравнения Максвелла в их спектральном представлении, физические величины которых заданы в комплексной плоскости, и при переходе из ( t , x ) - в ( ω , k ) -пространство (где t — время, x — координата, ω — угловая частота , k — волновой вектор ) посредством преобразования Фурье получаются более простые уравнения без производных .
Логические основания
Расширение поля вещественных чисел до комплексных, как и любое другое расширение алгебраической структуры, ставит множество вопросов, основные из которых — это вопросы о том, как определить операции над новым типом чисел, какие свойства будут иметь новые операции и (главный вопрос) допустимо ли такое расширение, не приведёт ли оно к неустранимым противоречиям.
Для анализа подобных вопросов в теории комплексных чисел надо сформировать набор аксиом.
Аксиоматика комплексных чисел
Можно определить аксиоматику множества комплексных чисел , если опираться на аксиоматическую теорию вещественных чисел . А именно, определим как минимальное поле , содержащее множество вещественных чисел и по меньшей мере одно число, вторая степень которого равна −1, — мнимую единицу . Говоря более строго, аксиомы комплексных чисел следующие .
- С1 : Для всяких комплексных чисел определена их сумма
- С2 : Сложение коммутативно : Далее в некоторых аксиомах для краткости будем опускать оговорку «для всяких ».
- С3 : Сложение ассоциативно :
- С4 : Существует элемент 0 (ноль) такой, что
- С5 : Для всякого комплексного числа существует противоположный ему элемент такой, что
- С6 : Для всяких комплексных чисел определено их произведение
- С7 : Умножение коммутативно :
- С8 : Умножение ассоциативно :
- С9 : Умножение связано со сложением распределительным (дистрибутивным) законом:
- С10 : Существует элемент 1 (единица), не равный нулю и такой, что
- С11 : Для всякого ненулевого числа существует обратное ему число такое, что
- С12 : Множество комплексных чисел содержит подполе, изоморфное полю вещественных чисел Для простоты далее это подполе обозначается той же буквой
- С13 : Существует элемент ( мнимая единица ) такой, что
- С14 ( аксиома минимальности ): Пусть — подмножество которое: содержит и мнимую единицу и замкнуто относительно сложения и умножения. Тогда совпадает со всем
Из этих аксиом вытекают как следствия все прочие свойства. Первые 11 аксиом означают, что образует поле, а 12-я аксиома устанавливает, что это поле является расширением Приведённая аксиоматика категорична , то есть любые её модели изоморфны .
Существуют и другие варианты аксиоматики комплексных чисел. Например, вместо того, чтобы опираться на уже построенное упорядоченное поле вещественных чисел, можно в качестве базы использовать аксиоматику теории множеств .
Непротиворечивость и модели
Стандартный способ доказать непротиворечивость новой структуры — смоделировать ( интерпретировать ) её аксиомы с помощью объектов другой структуры, чья непротиворечивость сомнений не вызывает. В нашем случае мы должны реализовать эти аксиомы на базе вещественных чисел .
Стандартная модель
Рассмотрим всевозможные упорядоченные пары вещественных чисел. В данной модели каждая такая пара будет соответствовать комплексному числу
Далее определим :
- пары и считаются равными, если и
- сложение : сумма пар и определяется как пара
- умножение : произведение пар и определяется как пара
Пояснение: сложное, на первый взгляд, определение умножения легко выводится из соотношения
Несложно убедиться, что описанная структура пар образует поле и удовлетворяет всему приведённому перечню аксиом комплексных чисел. Вещественные числа моделируются парами , образующими подполе , причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Пары и соответствуют нулю и единице поля. Такой способ является частным случаем процедуры Кэли — Диксона .
Мнимая единица — это пара Квадрат её равен то есть Любое комплексное число можно записать в виде
Описанная модель доказывает, что приведённая аксиоматика комплексных чисел непротиворечива. Потому что если бы в ней было противоречие, то это означало бы противоречие и в базовой для данной модели арифметике вещественных чисел, которую мы заранее предположили непротиворечивой .
Матричная модель
Комплексные числа можно также определить как подкольцо кольца вещественных матриц 2×2 вида
с обычным матричным сложением и умножением . Вещественной единице будет соответствовать
мнимой единице —
- .
Множество таких матриц является двумерным векторным пространством . Умножение на комплексное число является линейным оператором . В базисе линейный оператор умножения на представляется указанной выше матрицей, так как :
Матричная модель позволяет легко продемонстрировать связь между комплексными числами и линейными преобразованиями плоскости определённого типа. А именно, существует взаимно однозначное соответствие между комплексными числами и поворотными гомотетиями плоскости ( комбинациями растяжения относительно точки и поворота ): каждая поворотная гомотетия может быть представлена на комплексной плоскости как умножение на комплексное число .
Модель факторкольца многочленов
Рассмотрим кольцо многочленов с вещественными коэффициентами и построим его факторкольцо по модулю многочлена (или, что то же, по идеалу , порождённому указанным многочленом). Это значит, что два многочлена из мы будем считать эквивалентными , если при делении на многочлен они дают одинаковые остатки. Например, многочлен будет эквивалентен константе многочлен будет эквивалентен и т. д.
Множество классов эквивалентности образует кольцо с единицей. Так как многочлен неприводим , то это факторкольцо является полем. Роль мнимой единицы играет многочлен поскольку квадрат его (см. выше) эквивалентен Каждый класс эквивалентности содержит остаток вида (от деления на ), который в силу сказанного можно записать как Следовательно, это поле изоморфно полю комплексных чисел .
Данный изоморфизм был обнаружен Коши в 1847 году. Этот подход может быть использован для построения обобщений комплексных чисел, таких как алгебры Клиффорда .
Расширенное комплексное поле как фактор-поле рациональных дробей полиномов с вещественными коэффициентами
Нетривиальная факторизация поля в поле невозможна, но поля, расширенные бесконечностью, могут нетривиально факторизоваться. Более того, возможны нетривиальные факторизации обычных полей в расширенные. В частности, обычное или расширенное поле рациональных дробей полиномов одной переменной с вещественными коэффициентами факторизуется в расширенное поле комплексных чисел ( сферу Римана ) путём отождествления полинома с нулём. Каждая дробь при этом заменяется на частное остатков от деления числителя и знаменателя своего несократимого представления на . В силу несократимости, при этом не может образоваться неопределённость , в остальных случаях знаменатель, равный нулю, означает бесконечность, случай знаменателя, не равного нулю, рассматриваются в стандартной технике (домножением на сопряжённый знаменателю). Другим способом получения того же результата является параметризация полиномов числителя и знаменателя несократимого представления дроби мнимой единицей.
Параметризуя рациональные дроби полиномов различными числами, можно получать различные факторизации: при параметризации вещественным числом — расширенное поле вещественных, комплексным (не вещественным) — комплексных чисел. Число, используемое для параметризации, есть корень простого (над вещественным полем) полинома, отождествляемого с нулём, т. е. по модулю которого берутся числители и знаменатели (в случае вещественного числа — первой степени, комплексного — квадратный с отрицательным дискриминантом и, соответственно, двумя сопряжёнными комплексными корнями).
Алгебраическая характеризация
Как уже упоминалось , поле комплексных чисел алгебраически замкнуто и имеет характеристику ноль (из последнего свойства вытекает, что оно содержит подполе рациональных чисел ). Кроме того, любой базис трансцендентности над имеет мощность континуум . Этих трёх свойств достаточно, чтобы задать поле комплексных чисел с точностью до изоморфизма полей — между любыми двумя алгебраически замкнутыми полями характеристики 0 с континуальным базисом трансцендентности существует некоторое отождествление, согласованное с операциями сложения и умножения этих полей .
При этом отождествлении другие структуры, вроде нормы или топологии , могут не сохраняться. Например, алгебраическое замыкание поля -адических чисел также удовлетворяет трём указанным свойствам. Однако -адическая норма не является и, следовательно, не эквивалентна обычной норме комплексных чисел при любом выборе изоморфизма . Поэтому они задают различную структуру топологического векторного пространства : множество из любого элемента векторного пространства и его целозначных кратностей дискретно в комплексном случае и компактно — в -адическом .
Вариации и обобщения
Ближайшее обобщение комплексных чисел было обнаружено в 1843 году. Им оказалось тело кватернионов , которое, в отличие от поля комплексных чисел, содержит три мнимые единицы, традиционно обозначаемые Согласно теореме Фробениуса , комплексные числа являются одним из трёх возможных случаев конечномерной алгебры с делением над полем вещественных чисел. В 1919 году выяснилось, что и комплексные числа из вещественных, и кватернионы из комплексных чисел могут быть получены единой процедурой удвоения размерности , также известной как « процедура Кэли — Диксона » .
Дальнейшим применением этой процедуры образуются числа, описанные Артуром Кэли в 1845 году, до обнаружения этой процедуры, и названные « числами Кэли » (октонионы, октавы). Числа, получаемые следующим применением процедуры, названы седенионами . Несмотря на то, что эту процедуру можно повторять и далее, дальнейшие числа названий пока не имеют .
Другие типы расширений комплексных чисел ( гиперкомплексные числа ):
- Бикватернионы
- Комплексные числа гиперболического типа (двойные)
- Комплексные числа параболического типа (дуальные)
Примечания
- Комментарии
-
Два возможных ударения указаны согласно следующим источникам.
- Большая советская энциклопедия , 3-е изд. (1973), том 12, стр. 588, статья Ко́мпле́ксные числа .
- Советский энциклопедический словарь (1982), стр. 613, статья Ко́мпле́ксное число .
- Последнее издание «Словаря трудностей русского языка» (Розенталь Д. Э., Теленкова М. А., Айрис-пресс, 2005, стр. 273) указывает оба варианта: ко́мплексные (компле́ксные) числа .
- В Большой российской энциклопедии (том 14, 2010 год) приводятся варианты: Компле́ксное число (стр. 691, автор не указан), но от 2 июля 2019 на Wayback Machine (стр. 695, автор: член-корр. РАН Е. М. Чирка ).
- Орфографический словарь русского языка (изд. 6-е, 2010), Грамматический словарь русского языка, Русский орфографический словарь Российской академии наук под ред. В. В. Лопатина (изд. 4-е, 2013) и ряд других словарей указывают варианты: ко́мплексный и компле́ксный (матем.) .
- При условии непротиворечивости системы вещественных чисел.
- То есть отличается от (поля рациональных функций для набора переменных мощности континуум) на алгебраическое расширение
- Поскольку отображение в алгебраически замкнутое поле всегда может быть продлено на алгебраическое расширение, для установления изоморфизма между алгебраическими замкнутыми полями достаточно установить изоморфизм между их простыми подполями и биекцию между базисами трансцендентности.
- Использованная литература
- Краткий словарь иностранных слов. — 7-е изд. — М. : Русский язык , 1984. — С. 121. — 312 с.
- ↑ Комплексное число // Математическая энциклопедия (в 5 томах). — М. : Советская Энциклопедия , 1979. — Т. 2. — С. 1007.
- , с. 227.
- , с. 211, подстрочное примечание.
- , с. 222.
- ↑ , с. 180—181.
- . Дата обращения: 16 января 2018. 31 марта 2018 года.
- Мнимое число // Математическая энциклопедия (в 5 томах). — М. : Советская Энциклопедия , 1982. — Т. 3. — С. 708.
- . Дата обращения: 16 января 2018. 31 марта 2018 года.
- , с. 2.
- , с. 72.
- ↑ , с. 237—239.
- , с. 61—66.
- ↑ Bunch, Bryan. . — Dover Publications, 1997. — 240 p. — (Dover Books on Mathematics). — ISBN 978-0486296647 .
- , с. 233—234.
- ↑ , с. 234—235, 239—240.
- от 16 марта 2018 на Wayback Machine . Пункт 152. Комплексная амплитуда (синусоидального электрического) тока — комплексная величина, модуль и аргумент которой равны соответственно амплитуде и начальной фазе данного синусоидального электрического тока.
- ↑ , с. 6—10.
- , с. 14—15.
- ↑ , с. 183—1851.
- ↑ , с. 15—16.
- , с. 7.
- Weisstein, Eric W. (англ.) на сайте Wolfram MathWorld .
- , с. 3—4.
- ↑ Клайн Моррис . Математика. Утрата определённости . — М. : Мир, 1984. — С. 138—139.
- ↑ Стиллвелл Д. Математика и ее история. — Москва-Ижевск: Институт компьютерных исследований, 2004. — С. 258—266. — 530 с.
- , с. 57—61.
- Юшкевич А. П. Леонард Эйлер. Жизнь и творчество // Развитие идей Леонарда Эйлера и современная наука. Сб. статей. — М. : Наука, 1988. — ISBN 5-02-000002-7 . — С. 15—47.
- Острая О. . Дата обращения: 30 ноября 2017.
- Ренэ Декарт. Геометрия. С приложением избранных работ П. Ферма и переписки Декарта. — М. — Л. : Гостехиздат , 1938. — С. 233. — 297 с. — (Классики естествознания).
- Глейзер Г. И. История математики в школе. IX—X классы. — М. : Просвещение, 1983. — С. 193. — 351 с.
- ↑ , с. 7—15.
- , с. 360.
- , с. 15—22.
- , с. 44.
- ↑ Заславский А. А. Геометрические преобразования. — 2-е изд.. — М. : МЦНМО, 2004. — С. 58. — 86 с. — ISBN 5-94057-094-1 .
- ↑ , с. 180—186.
- . e-maxx.ru . Дата обращения: 9 мая 2021. 7 мая 2021 года.
- . www.mathnet.ru . Дата обращения: 9 мая 2021. 9 мая 2021 года.
- , с. 43.
- , с. 10.
- ↑ , с. 17—18.
- , с. 12.
- , с. 165.
- , с. 249—251.
- , с. 167.
- Топологическое поле // Математическая энциклопедия (в 5 томах). — М. : Советская Энциклопедия , 1985. — Т. 5. — С. 386.
- , Глава 5.
- , с. 78.
- , с. 114—124.
- Дербишир, Джон. Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. — Астрель, 2010. — 464 с. — ISBN 978-5-271-25422-2 .
- , с. 14.
- Филиппов А. Ф. Введение в теорию дифференциальных уравнений. — Эдиториал УРСС, 2004. — 240 с. — ISBN 5354004160 .
- Разностное уравнение // . — М. : Советская Энциклопедия , 1984. — Т. 4. — С. 838. 21 января 2022 года.
- , Глава 5.
- , Глава 8.
- , с. 22—25.
- Маркушевич А. И. . — М. : Гостехиздат, 1954. — 52 с. — (Популярные лекции по математике, выпуск 13). 28 января 2018 года.
- Shao-Feng Bian, Hou-Pu Li. . Дата обращения: 28 января 2018. 29 января 2018 года.
- Лаврентьев М. А., Шабат Б. В. Проблемы гидродинамики и их математические модели. — М. : Наука, 1973.
- ↑ Ландау Л. Д., Лифшиц Е. М. Квантовая механика (нерелятивистская теория). — Издание 6-е, исправленное. — М. : Физматлит , 2004 . — 800 с. — («Теоретическая физика», том III). — ISBN 5-9221-0530-2 .
- Е. Вигнер. // УФН. — 1968. — Т. 93 . — С. 535—546 . — doi : .
- , с. 132—144.
- Молчанов А. П., Занадворов П. Н. Курс электротехники и радиотехники, глава «Линейные цепи». — BH V. — 608 с. — ISBN 978-5-9775-0544-4 .
- Афонский А. А., Дьяконов В. П. / Под ред. проф. В. П. Дьяконова. — М. : СОЛОН-Пресс, 2009. — С. . — ISBN 978-5-913-59049-7 .
- , с. 164—165.
- , с. 227—233.
- , с. 166.
- . Дата обращения: 13 февраля 2018. 6 февраля 2021 года.
- ↑ , с. 167—168.
- , с. 230—233.
- John Stillwell. . — Springer Science & Business Media, 2005-12-30. — С. 84—86. — 240 с. — ISBN 9780387290522 .
- ↑ Фаддеев Д. К. Лекции по алгебре. — М. : Наука, 1984. — С. 200—201. — 416 с.
- F. Brackx, R. Delanghe, H. Serras. . — Springer Science & Business Media, 2012-12-06. — С. 33. — 405 с. — ISBN 9789401120067 .
- David Marker. Model Theory: An Introduction, ISBN 978-0-387-22734-4 . Proposition 2.2.5. Springer Science & Business Media, 2002. См. также от 14 мая 2018 на Wayback Machine .
- William Weiss and Cherie D’Mello. от 13 апреля 2018 на Wayback Machine . Lemma 7: Any two algebraically closed fields of characteristic 0 and cardinality are isomorphic и комментарий после неё.
- ↑ p-адическое число // Математическая энциклопедия (в 5 томах). — М. : Советская Энциклопедия , 1977. — Т. 1. — С. 100. : « Это расширение есть пополнение поля рациональных чисел относительно неархимедова нормирования… Поле локально компактно ».
- ↑ Dickson, L. E. (1919), "On Quaternions and Their Generalization and the History of the Eight Square Theorem", Annals of Mathematics , Second Series, Annals of Mathematics, 20 (3): 155—171, doi : , ISSN , JSTOR
Литература
- Балк М. Б. , Балк Г. Д., Полухин А. А. Реальные применения мнимых чисел. — Киев: Радянська школа, 1988. — 255 с. — ISBN 5-330-00379-2 .
- Бронштейн И. Н. , Семендяев К. А. Справочник по математике для инженеров и учащихся втузов . — изд. 13-е. — М. : Наука, 1985. — 544 с.
- Бурбаки Н. Очерки по истории математики. — М. , 1963.
- Виленкин Н. Я. , Ивашов-Мусатов О. С. , Шварцбурд С. И. Алгебра и математический анализ для 11 класса. Учебное пособие. — Изд. 6-е. — М. : Просвещение, 1998. — 288 с. — ISBN 5-09-008036-4 .
- Выгодский М. Я. Справочник по элементарной математике. — М. : АСТ, 2006. — 509 с. — ISBN 5-17-009554-6 .
- Глазков Ю. А., Варшавский И. К., Гаиашвили М. Я. Комплексные числа. 9—11 классы. — М. : Экзамен, 2012. — 157 с. — ISBN 978-5-377-03467-4 .
- Евграфов М. А. Аналитические функции. — 2-е изд., перераб. и дополн. — М. : Наука , 1968. — 472 с.
- Кириллов А. А. Что такое число?. — М. , 1993. — 80 с. — ISBN 5-02-014942-3 .
- Лаврентьев М. А. , Шабат Б. В. Методы теории функций комплексного переменного. — 4-е изд. — М. : Наука , 1972 .
- // История математики / Под редакцией А. П. Юшкевича , в трёх томах. — М. : Наука, 1972. — Т. III.
- Нечаев В. И. Числовые системы. — М. : Просвещение, 1975. — 199 с.
- Привалов И. И. Введение в теорию функций комплексного переменного. — 13-е изд.. — М. : Физматлит , 1984. — 432 с.
- Свешников А. Г. , Тихонов А. Н. Теория функций комплексной переменной. — М. : Наука, 1967. — 304 с.
- Смирнов В. И. Курс высшей математики в трёх томах. — Изд. 10-е. — СПб. : БХВ-Петербург, 2010. — Т. 3, часть 2-я. — 816 с. — ISBN 978-5-9775-0087-6 .
- Соломенцев Е. Д. Функции комплексного переменного и их применения. — М. : Высшая школа, 1988. — 167 с. — ISBN 5-06-003145-6 .
- Энциклопедия элементарной математики (в 5 томах). — М. : Физматгиз, 1951. — Т. 1. — С. 160—168. — 448 с.
- Ahlfors Lars V. Complex analysis. An introduction to the theory of analytic functions of one complex variable. — Third edition. — Harvard University: McGraw-Hill Book Company, 1979. — 317 с. — ISBN 0-07-000657-1 .
Ссылки
-
Глейзер Г.
. Журнал «Математика». — № 10 (2001). Дата обращения: 18 апреля 2017.
- , «Математика» № 11 (2001).
- Понтрягин Л. // Квант . — 1982. — № 3 .
- . Дата обращения: 17 января 2018.
- , Йос Лейс, Орельян Альварез . . Главы 5 и 6: Комплексные числа. (рус.)
- 2021-03-15
- 1
























































































































































































![{\displaystyle z^{n}=\left[r\left(\cos \varphi +i\sin \varphi \right)\right]^{n}=r^{n}\left(\cos n\varphi +i\sin n\varphi \right),}](/images/004/912/4912684/190.jpg?rand=4908)




![{\displaystyle {\begin{alignedat}{2}z^{1/n}&=\left[r\left(\cos \left(\varphi +2\pi k\right)+i\sin \left(\varphi +2\pi k\right)\right)\right]^{1/n}=\\&={\sqrt[{n}]{r}}\left(\cos {\frac {\varphi +2\pi k}{n}}+i\sin {\frac {\varphi +2\pi k}{n}}\right),\\\end{alignedat}}}](/images/004/912/4912684/195.jpg?rand=669789)






![{\sqrt[ {n}]{r}}](/images/004/912/4912684/203.jpg?rand=1567)


![{\displaystyle {\sqrt[{3}]{2+11i}}}](/images/004/912/4912684/206.jpg?rand=273352)
















![{\displaystyle x={\sqrt[{3}]{2+11i}}+{\sqrt[{3}]{2-11i}}.}](/images/004/912/4912684/223.jpg?rand=488935)
![{\displaystyle {\sqrt[{3}]{2\pm 11i}}=2\pm i,}](/images/004/912/4912684/224.jpg?rand=477731)


















































































![{\displaystyle \left[{\hat {x}},{\hat {p}}_{x}\right]={\hat {x}}{\hat {p}}_{x}-{\hat {p}}_{x}{\hat {x}}=i\hbar \,.}](/images/004/912/4912684/308.jpg?rand=667093)




































































![\mathbb{R}[x]](/images/004/912/4912684/377.jpg?rand=624736)

![\mathbb{R}[x]](/images/004/912/4912684/379.jpg?rand=319378)