Степени свободы (теория вероятностей)
- 1 year ago
- 0
- 0
|
История теории вероятностей отмечена многими уникальными особенностями. Прежде всего, в отличие от появившихся примерно в то же время других разделов математики (например, математического анализа или аналитической геометрии ), у теории вероятностей по существу не было античных или средневековых предшественников, она целиком — создание Нового времени . Долгое время теория вероятностей считалась чисто опытной наукой и «не совсем математикой» , её строгое обоснование было разработано только в 1929 году, то есть даже позже, чем аксиоматика теории множеств (1922). В наши дни теория вероятностей занимает одно из первых мест в прикладных науках по широте своей области применения; «нет почти ни одной естественной науки, в которой так или иначе не применялись бы вероятностные методы» .
Историки выделяют в развитии теории вероятностей несколько периодов .

Первые задачи вероятностного характера возникли в различных азартных играх — костях , картах и др. Французский каноник XIII века Ришар де Фурниваль правильно подсчитал все возможные суммы очков после броска трёх костей и указал число способов, которыми может получиться каждая из этих сумм. Это число способов можно рассматривать как первую числовую меру ожидаемости события, аналогичную вероятности. До Фурниваля, а иногда и после него, эту меру часто подсчитывали неверно, считая, например, что суммы 3 и 4 очка равновероятны, так как оба могут получиться «только одним способом»: по результатам броска «три единицы» и «двойка с двумя единицами» соответственно. При этом не учитывалось, что три единицы в самом деле получаются только одним способом: , а двойка с двумя единицами — тремя: , так что эти события не равновероятны . Аналогичные ошибки неоднократно встречались и в дальнейшей истории науки.
В обширной математической энциклопедии «Сумма арифметики, геометрии, отношений и пропорций» итальянца Луки Пачоли (1494) содержатся оригинальные задачи на тему: как разделить ставку между двумя игроками, если серия игр прервана досрочно. Пример подобной задачи: игра идёт до 60 очков, победитель получает всю ставку в 22 дуката , в ходе игры первый игрок набрал 50 очков, второй — 30, и тут игру пришлось прекратить; требуется справедливо разделить исходную ставку. Решение зависит от того, что понимать под «справедливым» разделом; сам Пачоли предложил делить пропорционально набранным очкам (55/4 и 33/4 дуката) ; позднее его решение было признано ошибочным .

Крупный алгебраист XVI века Джероламо Кардано посвятил анализу игры содержательную монографию «Книга об игре в кости» (1526 год, опубликована посмертно). Кардано провёл полный и безошибочный комбинаторный анализ для значений суммы очков и указал для разных событий ожидаемое значение доли «благоприятных» событий: например, при бросании трёх костей доля случаев, когда значения всех 3 костей совпадают, равна 6/216 или 1/36. Кардано сделал проницательное замечание: реальное количество исследуемых событий может при небольшом числе игр сильно отличаться от теоретического, но чем больше игр в серии, тем доля этого различия меньше. По существу, Кардано близко подошёл к понятию вероятности :
Итак, имеется одно общее правило для расчёта: необходимо учесть общее число возможных выпадений и число способов, которыми могут появиться данные выпадения, а затем найти отношение последнего числа к числу оставшихся возможных выпадений.
Другой итальянский алгебраист, Никколо Тарталья , раскритиковал подход Пачоли к решению задачи о разделе ставки: ведь если один из игроков ещё не успел набрать ни одного очка, то алгоритм Пачоли отдаёт всю ставку его сопернику, но это трудно назвать справедливым, поскольку некоторые шансы на выигрыш у отстающего всё же имеются. Кардано и Тарталья предложили свои (различные) способы раздела, но впоследствии и эти способы были признаны неудачными .
Исследованием данной темы занимался и Галилео Галилей , написавший трактат «О выходе очков при игре в кости» (1718 год, опубликован посмертно). Изложение теории игры у Галилея отличается исчерпывающей полнотой и ясностью. В своей главной книге « Диалог о двух главнейших системах мира , птолемеевой и коперниковой» Галилей также указал на возможность оценки погрешности астрономических и иных измерений, причём заявил, что малые ошибки измерения вероятнее, чем большие, отклонения в обе стороны равновероятны, а средний результат должен быть близок к истинному значению измеряемой величины. Эти качественные рассуждения стали первым в истории предсказанием нормального распределения ошибок .

В XVII веке начало формироваться отчётливое представление о проблематике теории вероятностей и появились первые математические ( комбинаторные ) методы решения вероятностных задач. Основателями математической теории вероятностей стали Блез Паскаль и Пьер Ферма .
Перед этим математик-любитель шевалье де Мере обратился к Паскалю по поводу так называемой «задачи об очках»: сколько раз нужно бросать две кости, чтобы ставить на одновременное выпадение хотя бы раз двух шестёрок было выгодно? Паскаль и Ферма вступили в переписку друг с другом по поводу данной задачи и родственных вопросов ( 1654 ). В рамках этой переписки учёные обсудили ряд проблем, связанных с вероятностными расчётами; в частности, рассматривалась старая задача о разделе ставки, и оба учёных пришли к решению, что надо разделить ставку соответственно остающимся шансам на выигрыш. Паскаль указал де Мере на ошибку, допущенную им при решении «задачи об очках»: в то время как де Мере неверно определил равновероятные события, получив ответ: 24 броска, Паскаль дал правильный ответ: 25 бросков .
Паскаль в своих трудах далеко продвинул применение комбинаторных методов, которые систематизировал в своей книге «Трактат об арифметическом треугольнике » (1665) . Опираясь на вероятностный подход, Паскаль даже доказывал (в посмертно опубликованных заметках), что быть верующим выгоднее, чем атеистом (см. « пари Паскаля »).

Тематика дискуссии Паскаля и Ферма (без подробностей) стала известна Христиану Гюйгенсу , который опубликовал собственное исследование «О расчётах в азартных играх» ( 1657 ): первый трактат по теории вероятностей . В предисловии Гюйгенс пишет :
Я полагаю, что при внимательном изучении предмета читатель заметит, что имеет дело не только с игрой, но что здесь закладываются основы очень интересной и глубокой теории.
В трактате Гюйгенса подробно излагаются вопросы, рассмотренные Ферма и Паскалем, но ставятся и новые вопросы . Главным достижением нидерландского учёного стало введение понятия математического ожидания , то есть теоретического среднего значения случайной величины . Гюйгенс также указал классический способ его подсчёта :
Если число случаев, в которых получается сумма , равно , а число случаев, в которых получается сумма , равно , то стоимость моего ожидания равна .
Гюйгенс, как видно из цитаты, вначале использовал термин «стоимость», а термин «ожидание» появился впервые при переводе трактата Гюйгенса Ван Схоутеном на латинский язык и стал общепринятым в науке .
В книге большое число задач, некоторые с решениями, другие «для самостоятельного решения». Из последних особый интерес и оживлённое обсуждение вызвала « задача о разорении игрока ». В несколько обобщённом виде она формулируется так: у игроков A и B есть и монет соответственно, в каждой игре выигрывается одна монета, вероятность выигрыша A в каждой игре равна требуется найти вероятность полного его разорения. Полное общее решение «задачи о разорении» дал Абрахам де Муавр полвека спустя (1711) . В наши дни вероятностная схема «задачи о разорении» используется при решении многих задач типа « случайное блуждание » .
Гюйгенс проанализировал и задачу о разделе ставки, дав её окончательное решение: ставку надо разделить пропорционально вероятностям выигрыша при продолжении игры . Он также впервые применил вероятностные методы к демографической статистике и показал, как рассчитать среднюю продолжительность жизни .
К этому же периоду относятся публикации английских статистиков Джона Граунта (1662) и Уильяма Петти (1676, 1683). Обработав данные более чем за столетие, они показали, что многие демографические характеристики лондонского населения, несмотря на случайные колебания, имеют достаточно устойчивый характер — например, соотношение числа новорождённых мальчиков и девочек редко отклоняется от пропорции 14 к 13, невелики колебания и процента смертности от конкретных случайных причин. Эти данные подготовили научную общественность к восприятию новых идей .
Граунт также впервые составил таблицы смертности — таблицы вероятности смерти как функции возраста. Вопросами теории вероятностей и её применения к демографической статистике занялись также Иоганн Худде и Ян де Витт в Нидерландах, которые в 1671 году также составили таблицы смертности и использовали их для вычисления размеров пожизненной ренты . Более подробно данный круг вопросов был изложен в 1693 году Эдмундом Галлеем .
На книгу Гюйгенса опирались появившиеся в начале XVIII века трактаты Пьера де Монмора «Опыт исследования азартных игр» ( фр. Essay d'analyse sur les jeux de hazard ; опубликован в 1708 и переиздан с дополнениями в 1713 году) и Якоба Бернулли «Искусство предположений» ( лат. Ars conjectandi ; опубликован уже после смерти учёного, в том же 1713 году). Последний имел для теории вероятностей особенно большое значение .

Над трактатом «Искусство предположений» Якоб Бернулли работал двадцать лет, уже лет за десять до публикации текст этого труда в виде незаконченной рукописи стал распространяться по Европе, вызывая большой интерес. Трактат стал первым систематическим изложением теории вероятностей. В этой книге автор привёл, в частности, классическое определение вероятности события как отношения числа исходов, связанных с этим событием, к общему числу исходов (у достоверного события вероятность равна единице, у невозможного — нулю). Систематически изученная Бернулли вероятностная схема сейчас называется биномиальным распределением .
Ранее математики чаще всего оперировали самим количеством исходов; историки полагают, что замена количества на «частоту» (то есть деление на общее количество исходов) была стимулирована статистическими соображениями: частота, в отличие от количества, обычно имеет тенденцию к стабилизации при увеличении числа наблюдений. Определение вероятности «по Бернулли» сразу стало общепринятым, его воспроизводили Абрахам де Муавр в книге «Учение о случаях» (1718) и все последующие математики. Единственное важное уточнение — о том, что все «элементарные исходы» обязаны быть равновероятны, — сделал Пьер-Симон Лаплас в 1812 году. Если для события невозможно подсчитать классическую вероятность (например, из-за отсутствия возможности выделить равновероятные исходы), то Бернулли предложил использовать статистический подход, то есть оценить вероятность по результатам наблюдений этого события или связанных с ним .

В первой части своего трактата Бернулли полностью перепечатывает книгу Гюйгенса, которой он даёт самую высокую оценку, и существенно дополняет собственными комментариями. В частности, он приводит общую « формулу Бернулли »: если вероятность события равна , то вероятность того, что в испытаниях событие случится раз, равна . Далее Бернулли подробно излагает комбинаторику и на её основе решает несколько задач со случайным выбором. В последней части книги, оставшейся недописанной, Бернулли собирался рассмотреть экономические и другие практические приложения теории вероятностей .
Огромное значение как для теории вероятностей, так и для науки в целом имел доказанный Бернулли первый вариант закона больших чисел (название закону дал позже Пуассон ) . Этот закон объясняет, почему статистическая частота при увеличении числа наблюдений сближается с теоретическим её значением — вероятностью, и тем самым связывает два разных определения вероятности. В дальнейшем закон больших чисел трудами многих математиков был значительно обобщён и уточнён; как оказалось, стремление статистической частоты к теоретической отличается от стремления к пределу в анализе — частота может значительно отклоняться от ожидаемого предела, и можно только утверждать, что вероятность таких отклонений с ростом числа испытаний стремится к нулю. Вместе с тем отклонения частоты от вероятности также поддаются вероятностному анализу .

Трактат Якоба Бернулли вызвал резкий подъём интереса к вероятностным проблемам и рост числа исследований новых задач. Абрахам де Муавр опубликовал несколько работ, среди которых наиболее интересны статья «Об измерении случайности, или вероятностях результатов в азартных играх» (1711) и трактат «Учение о случаях» (1718), выдержавший в XVIII веке три издания. В этом трактате Муавр не только полностью решил упоминавшуюся выше «задачу о разорении игрока», но и оценил для неё среднюю продолжительность игры и вероятности выигрыша за заданное число игр для каждого игрока . В другой работе, называвшейся «Аналитическая смесь», Муавр дал первый вариант теоремы Муавра—Лапласа , исследующей распределение возможных отклонений статистической частоты от вероятности. Муавр рассмотрел только случай, когда вероятность равна 1/2, общий же случай для любой вероятности доказал Лаплас . Ещё одним достижением Муавра стало первое введение в науку нормального распределения (1733), которое появилось у него как аппроксимация биномиального распределения .
Даниил Бернулли , племянник основателя теории вероятностей, также внёс вклад в эту науку. Он, независимо от Муавра, исследовал нормальное распределение для ошибок наблюдений, первым применил к вероятностным задачам методы математического анализа , опубликовал первый из вероятностных парадоксов (1738) .
Следующий важный шаг сделал английский математик Томас Симпсон , который в ходе занятий численным анализом в книге «Природа и законы случая» (1740) фактически использовал третье (наряду с классическим и статистическим) определение вероятности — геометрическое, пригодное для исследования непрерывных случайных величин с бесконечным числом значений. В задаче XXVI Симпсон нашёл вероятность того, что наудачу брошенный на плоскость параллелепипед остановится на заданной своей грани .

Подход Симпсона развил Жорж-Луи де Бюффон , который в 1777 году привёл классический пример задачи на геометрическую вероятность . Это была занимавшая впоследствии многих математиков « задача Бюффона о бросании иглы »: плоскость разграфлена «в линейку», на неё наудачу бросается игла, требуется найти вероятность того, что игла пересечёт линию . Если длина иглы меньше, чем расстояние между линиями , то искомая вероятность равна . Данная формула была несколько раз проверена экспериментально, в том числе самим Бюффоном, а в 1901 году итальянский математик Марио Лаццарини (Mario Lazzarini) использовал её для опытного определения числа . Задача Бюффона, её анализ и различные модификации обсуждались математиками многие годы .
Была решена важнейшая задача расчёта вероятности для сложных событий. Английский математик Томас Байес первым в отчётливом виде привёл теорему сложения вероятностей для нескольких несовместимых событий и основополагающие в теории вероятностей и статистике « формулы Байеса » (1763 год, опубликованы посмертно). В современной терминологии формулы Байеса позволяют рассчитать условную вероятность , а также уточнить рассчитанную вероятность после получения новых данных. Теорему умножения вероятностей ранее открыл Муавр (1718 год) и дал ей вполне современную, хотя и словесную формулировку: «вероятность появления двух зависимых событий равна произведению вероятности появления одного из них на вероятность того, что другое должно появиться, если первое из них уже появилось» .
К середине XVIII века анализ игр всё ещё привлекает некоторый интерес — например, Леонард Эйлер дал подробный анализ разных типов лотерей , но центром внимания математиков всё в большей степени становятся демографическая статистика , страхование и оценка ошибок (измерения, округления и т. п.). Статистике и страхованию Эйлер посвятил немало работ; он, в частности, решал задачу: оценить по статистическим таблицам, какова вероятность того, что человек в возрасте лет проживёт ещё лет .
В XIX веке число работ по теории вероятностей продолжало расти, были даже компрометирующие науку попытки распространить её методы далеко за разумные пределы — например, на область морали, психологии, правоприменения и даже богословия . В частности, валлийский философ Ричард Прайс , а следом за ним и Лаплас , считали возможным рассчитать по формулам Байеса вероятность предстоящего восхода Солнца , Пуассон пытался провести вероятностный анализ справедливости судебных приговоров и достоверности показаний свидетелей . Философ Дж. С. Милль в 1843 году, указав на подобные спекулятивные применения, назвал исчисление вероятностей «позором математики» . Эта и другие оценки свидетельствовали о недостаточной строгости обоснования теории вероятностей.
Математический аппарат теории вероятностей тем временем продолжал совершенствоваться. Основной сферой её применения в тот период была математическая обработка результатов наблюдений, содержащих случайные погрешности, а также расчёты рисков в страховом деле и других статистических параметров. Среди главных прикладных задач теории вероятностей и математической статистики XIX века можно назвать следующие :
Уже к середине XIX века формируется вероятностная теория артиллерийской стрельбы. В большинстве крупных стран Европы были созданы национальные статистические организации. В конце века область применения вероятностных методов начала успешно распространяться на физику, биологию, экономику, социологию .

Карл Фридрих Гаусс , постоянно занимавшийся астрономическими вычислениями, разработал вероятностную методику работы с измерениями, содержащими погрешности (1809). Он глубоко изучил нормальное распределение , показал, что оно во многих практических ситуациях является предельным для случайных значений, обосновал применение метода наименьших квадратов для оценки измеряемого значения и параметров его возможного диапазона разброса. Окончательную версию теории Гаусс изложил в двух трудах «Теория комбинации наблюдений, подверженных случайным ошибкам» (1823, 1828) . Хотя нормальный закон был известен задолго до Гаусса, его вклад в теорию этого важнейшего распределения настолько велик, что долгое время нормальный закон называли «законом Гаусса»; современный термин закрепился благодаря работам Карла Пирсона в конце XIX века .
Основные достижения теории вероятностей подытожены в капитальной монографии Лапласа «Аналитическая теория вероятностей» (1812 год), которая завершила «классический этап» развития этой науки. В XIX веке труд Лапласа выдержал во Франции три переиздания и был переведён на многие языки мира . Лаплас исследовал как дискретные, так и непрерывные случайные величины (ещё не вводя термина «случайная величина»), причём для непрерывных дал ключевое понятие плотности распределения вероятности , ранее неявно и ограниченно использованное Даниилом Бернулли. Интегральное понятие функции распределения возникло гораздо позже (его в 1912 году ввёл А. М. Ляпунов ); общий термин «случайная величина» также, по-видимому, впервые появился в работах русской вероятностной школы . Введение плотности вероятности и характеристических функций позволило Лапласу применить для решения вероятностных задач мощные аналитические средства, включая дифференциальные уравнения в частных производных .
Лаплас привёл формулу полной вероятности для нескольких несовместных «причин» (в современной терминологии, «гипотез»), доказал ряд предельных теорем, в том числе теорему Муавра—Лапласа и сходимость биномиального распределения к нормальному при увеличении числа испытаний. Значительная часть книги посвящена статистическим приложениям и решению задач. Для оценки возможного диапазона значений измеряемой величины Лаплас, как и Гаусс, рекомендовал метод наименьших квадратов .
Лаплас описал и своё понимание сущности случайности и вероятности. По его мнению, ход реальных процессов полностью предопределён ( «детерминирован» ), случайность появляется лишь в человеческом восприятии и только там, где человек не владеет полным знанием происходящего :
Ум, которому были бы известны для какого-либо данного момента все силы, одушевляющие природу, и относительное положение всех её составных частей, если бы вдобавок он оказался достаточно обширным, чтобы подчинить эти данные анализу, обнял бы в одной формуле движение величайших тел вселенной наравне с движениями легчайших атомов; не осталось бы ничего, что было бы для него недостоверно, и будущее, так же, как и прошедшее, предстало бы пред его взором.
Симеон Дени Пуассон в 1837 году обобщил закон больших чисел Бернулли, сняв условие о том, что вероятность события в каждой игре одна и та же; при этих новых условиях статистическая частота будет сходиться к среднему арифметическому для вероятностей отдельных игр . Он же опубликовал формулу Пуассона , удобную для описания схемы Бернулли в том случае, когда вероятность события близка к нулю или к единице. Распределение Пуассона («закон редких событий») является одним из основных в прикладных задачах, например, ему подчиняются радиоактивный распад , рождение тройни, статистика аварий и несчастных случаев .
Основная проблема в этой области следующая. Пусть последовательные измерения некоторой величины дали близких, но неравных значений. Подразумевается, что систематические ошибки и зависимость величины от времени измерения (скажем, при вращении небесного свода ) учтены, так что различие данных вызвано чисто случайными погрешностями. Надо по результатам измерений найти наилучшую оценку истинного значения исследуемой величины .
Первое математическое исследование этой практически важной (особенно в астрономии) темы предпринял Томас Симпсон (1755). Он исходил из неверной гипотезы, что ошибки измерения распределены по «треугольному закону», но сделал правильный вывод — среднее арифметическое результатов измерения ближе к истинному значению, чем отдельное измерение. Даниил Бернулли (1778) считал, что плотность распределения ошибок представляет собой дугу окружности, но вывод Симпсона подтвердил . Идеи Симпсона развил И. Г. Ламберт , впервые применивший метод производящих функций и метод максимального правдоподобия , позднее обобщённый Р. Э. Фишером .
В XIX веке Лаплас указал, что наблюдаемые погрешности измерения являются обычно результатом суммирования множества случайных ошибок, и поэтому их распределение должно быть близко к нормальному . Вместо среднего арифметического он предложил статистическую медиану . Однако почти одновременно был опубликован гораздо более практичный метод наименьших квадратов Гаусса (1809), который и стал общеупотребительным. В 1853 году Коши обнаружил пример распределения , для которого среднее арифметическое является очень плохой оценкой. К концу XIX века статистическая теория обработки ошибок была в основном завершена .
В 1889 году французский математик Жозеф Бертран в своём курсе «Анализ вероятностей» предложил ряд парадоксов , связанных с геометрической вероятностью. В каждом парадоксе разное истолкование понятий «наудачу» или «взятое произвольно» приводило к разным решениям задачи. Пример одного из парадоксов Бертрана: найти вероятность того, что выбранная наудачу хорда окружности окажется длиннее стороны вписанного в эту окружность треугольника. При разных методах выбора хорды «наудачу» получаются разные ответы.
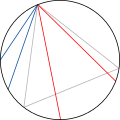
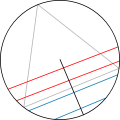
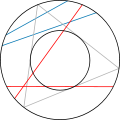
Обсуждение парадоксов Бертрана содействовало уточнению оснований теории вероятностей и смысла термина «равновероятно» .

До середины XIX века практическое применение теории вероятностей было в основном ограничено статистикой и приближёнными вычислениями , поэтому общий термин «случайная величина» появился довольно поздно . Одним из первых случайных процессов в физике стало изученное Робертом Броуном в 1827 году под микроскопом хаотическое движение цветочной пыльцы, плававшей в воде (« броуновское движение »). Его математическая модель , однако, появилась только в начале XX века ( А. Эйнштейн , М. Смолуховский , Н. Винер ) .
Первые физические вероятностные модели возникли в статистической физике , которую разработали во второй половине XIX века Л. Больцман , Д. К. Максвелл и Д. У. Гиббс . Больцман в серии работ (1870-е годы) показал, что термодинамические законы имеют вероятностно-статистический характер и связаны с переходом физических систем из менее вероятного состояния в более вероятное, причём мерой вероятности является энтропия . Максвелл в эти же годы вывел закон распределения скоростей молекул в газе, который позволяет рассчитать энергию , длину свободного пробега и другие характеристики молекул. В 1902 году Гиббс опубликовал монографию «Основные принципы статистической механики», оказавшую большое влияние на развитие физики . К концу XIX века огромное практическое значение вероятностных методов стало общепризнанным фактом.
В России в первой половине XIX века начали возникать собственные серьёзные исследования по теории вероятностей. Первый учебный курс начал читать С. Ревковский в Вильнюсском университете (1829 год), там же в 1830 году была создана первая в Российской империи кафедра теории вероятностей. В Петербургском университете лекции с 1837 года читал сначала В. А. Анкудович , а с 1850 года — В. Я. Буняковский . Фундаментальный учебник «Основания математической теории вероятностей» Буняковский опубликовал в 1846 году, и придуманная им русская терминология стала общепринятой. В Московском университете курс появился в 1850 году, лекции читал А. Ю. Давидов , будущий президент Московского математического общества .
Статьи по вероятностным темам публиковали многие крупные математики России, в том числе М. В. Остроградский , Н. Д. Брашман , Н. И. Лобачевский , Н. Е. Зернов . В значительной части этих работ ощущается сильное влияние трудов и взглядов Лапласа .

Первыми русскими математиками мирового уровня в теории вероятностей стали П. Л. Чебышёв и его ученики А. А. Марков и А. М. Ляпунов . Чебышёв с самого начала своей научной карьеры уделял наибольшее внимание теории вероятностей (наряду с теорией чисел ), а с 1860 года сменил Буняковского на кафедре теории вероятностей и начал свой цикл лекций. Он опубликовал по данной теме всего четыре работы, но фундаментального характера. Особенно интересна его статья «О средних величинах» (1866 год), где приведено « неравенство Чебышёва », позднее усиленное Марковым :

Эта формула означает, что вероятность отклонения любой случайной величины от её среднего значения ( математического ожидания ) более чем на стандартных отклонений ( ) не превышает . Например, отклонение на 5 имеет вероятность не более 1/25, то есть не более 4 %.
В качестве следствия своего неравенства Чебышёв получил чрезвычайно общую формулировку закона больших чисел : если математические ожидания серии случайных величин и квадраты этих математических ожиданий ограничены в совокупности, то среднее арифметическое этих величин с ростом сходится к среднему арифметическому для их математических ожиданий. Из этой теоремы получаются как следствия теоремы Бернулли и Пуассона; Чебышёв впервые строго оценил точность этих теорем и других приближений .
В 1887 году появилась статья Чебышёва «О двух теоремах относительно вероятностей». В этой работе он установил, что при некоторых (достаточно общих) условиях выполняется предельная теорема: сумма большого числа независимых случайных величин (например, погрешностей измерения) распределена приближённо по нормальному закону и тем точнее, чем больше слагаемых. Этот результат по своей общности далеко перекрывает теорему Муавра — Лапласа и все её аналоги . Позже А. А. Марков и А. М. Ляпунов уточнили и ещё более обобщили данную теорему Чебышёва.
Обе упомянутые теоремы Чебышёва занимают центральное место в теории вероятностей. Особенно важно то обстоятельство, что Чебышёв не только указал предельное распределение, но в обоих случаях детально проанализировал границы возможных отклонений от этого предела .
Если Чебышёв исследовал независимые случайные величины, то А. А. Марков в 1907 году расширил поле исследований, рассматривая и случай, когда новое случайное значение зависит от старого. Марков доказал вариант закона больших чисел для некоторых распространённых типов зависимых величин, введя в терминологию мировой науки « цепи Маркова ». Анализу и классификации этих цепей Марков посвятил немало работ; цепи Маркова и марковские случайные процессы применяются не только в математике, но и в других науках, таких как статистическая физика , квантовая механика , теория автоматического управления и многие другие . Маркову принадлежит также вероятностное обоснование метода наименьших квадратов .
А. М. Ляпунову принадлежит введение метода характеристических функций в учение о предельных теоремах теории вероятностей .
В XX веке исследования Чебышёва и Маркова продолжили А. Я. Хинчин , А. Н. Колмогоров и др. В частности, Ярл В. Линдеберг (1922) и Колмогоров (1926) нашли условия, необходимые и достаточные для выполнения закона больших чисел .
Математический аппарат теории вероятностей значительно обогатился во многих направлениях. После разработки теории меры это общее понятие оказалось удобно применить к теории вероятностей, то есть рассматривать вероятность как меру (конечного или бесконечного) множества «благоприятных событий». Такой подход позволяет описывать и исследовать свойства вероятности на хорошо разработанном языке теории множеств .

В теории динамических систем было обнаружено, что решения дифференциальных уравнений некоторых систем ведут себя как случайные процессы . Это крупное открытие привело к созданию понятия « динамический хаос » и общей «теории хаоса» . Одним из примеров является « задача трёх тел » небесной механики .
До XX века использовались в основном нормальное, биномиальное и (иногда) пуассоновское распределения , однако практически полезными оказались и многие другие теоретические законы . Например, логнормальное распределение часто встречается в ситуациях, когда исследуемая величина есть произведение нескольких независимых положительных случайных величин .
Вероятностные методы оказались плодотворными во многих областях теоретической и прикладной математики, даже в таких классических, как теория чисел или логика . В свою очередь, современная теория вероятностей использует методы и подходы, разработанные в функциональном анализе , топологии и других разделах математики, появившихся в XX веке .

Применением в статистике математических методов, в том числе специально разработанных для этой цели, занимались многие учёные, от Гюйгенса и Лапласа до Кетле и Гальтона . Математическая статистика как основа для принятия надёжных решений о случайных величинах возникла на рубеже XIX—XX веков благодаря основополагающим работам Карла Пирсона , ученика Гальтона. Пирсон разработал теорию корреляции , критерии согласия , регрессионный анализ , алгоритмы проверки гипотез , принятия решений и оценки параметров . Алгоритмы, предложенные Пирсоном, находят широкое применение в физике, медицине, биологии, социологии, сельском хозяйстве и др.
Виднейшим продолжателем работ Пирсона по прикладной математической статистике в первой половине XX века стал Рональд Эйлмер Фишер . Он опубликовал работы по планированию эксперимента , разработал метод максимального правдоподобия , тест статистической значимости , дисперсионный анализ и решение ряда других практически важных статистических проблем. Совместно с Ежи Нейманом разработал концепцию доверительного интервала (1937). Фишер — автор общепризнанного термина « дисперсия случайной величины » ( англ. variance ) .
Начиная примерно с 1920-х годов, быстро развивается теория статистического контроля качества промышленной продукции. Первую проблему по этой теме рассмотрел ещё Томас Симпсон в 1846 году. В массовом производстве надо определить, по какой методике следует изъять предметы из одной или нескольких партий продукции для проверки их качества .
Изобилие в наши дни статистических исследований, нередко дающих противоположные результаты (например, о наличии или отсутствии вреда от мобильных телефонов или генно-модифицированных продуктов ), сделало актуальной и часто обсуждаемой проблему обеспечения достоверных выводов из статистического обследования. Наиболее частая ошибка — объявление, что статистическая зависимость ( корреляция ) изучаемых факторов якобы свидетельствует о причинной связи между ними, хотя часто связь этих факторов реально объясняется их зависимостью от одного или нескольких третьих факторов . «Статистическая зависимость, как бы ни была она сильна, никогда не может установить причинной связи: наши идеи о причине должны приходить извне статистики, в конечном счёте из некоторой другой теории» .

Понятие случайного (или стохастического) процесса , возникшее в начале XX века, стало одним из центральных, быстро развивающихся и наиболее полезных применений теории вероятностей. Случайный процесс — это переменная во времени случайная величина. Первые исследования случайных процессов касались в основном электроники и сообщений теории связи , в наши дни можно привести в качестве примеров временные ряды в экономике или медицине, регистрограммы теории механизмов , статистику жизни биологии популяций . Широкую сферу практического применения имеет теория массового обслуживания . Среди типовых задач анализа случайных процессов :
Проведена классификация типов случайных процессов, разработаны аналитические средства их исследования ( корреляционная и ковариационная функции , спектральное разложение) . Для анализа процессов разработаны такие новые средства, как стохастические дифференциальные уравнения , стохастический интеграл , средства спектрального анализа и фильтрации .
Новые применения вероятностных методов возникали в XX веке постоянно и во многих науках; кратко перечислим некоторые этапные события в этой тенденции.
Центральным понятием созданной в 1920-е годы квантовой механики является комплексная волновая функция , квадрат модуля которой, согласно распространённой копенгагенской интерпретации , определяет плотность вероятности обнаружения микрочастицы в данной точке пространства. Если принять такую интерпретацию, то в математической модели микромира случайность неустранима, а лапласовский детерминизм полностью опровергнут . Для микромира были разработаны специальные квантовые статистики Бозе — Эйнштейна и Ферми — Дирака .
После открытий Менделя и Моргана стало понятно, что наследственные признаки передаются потомкам путём случайной комбинации одного из двух признаков ( аллелей ) от отца и одного из двух аналогичных аллелей от матери. Случайный выбор аллели отца определяет заодно пол будущего потомка. На этот процесс дополнительно накладываются случайные мутации , поэтому вероятностные методы легли в основу генетики . Применяются они также при исследовании и управлении развитием биологических популяций . Существенно используются вероятностные подходы (например, байесовские методы и методы, основанные на принципе наибольшего правдоподобия ) в , предусматривающей применение специальных вычислительных алгоритмов и компьютерных программ для построения филогенетических деревьев .
Теория информации опирается на введённое Клодом Шенноном в 1948 году понятие информационной энтропии . Если случайная величина может принимать значения , вероятности которых соответственно равны , то энтропия определяется формулой:
Определённая так энтропия есть мера случайности (или неопределённости): она равна нулю, если случайность отсутствует, то есть с вероятностью 1 величина принимает одно определённое значение. Увеличение случайности связано с увеличением энтропии .
Теория автоматического управления также изначально использовала вероятностные методы. С появлением компьютеров применение таких методов многократно расширилось. Используя генератор псевдослучайных чисел , можно промоделировать на компьютере случайные величины или процессы с произвольным распределением, а это, в свою очередь, позволяет исследовать самые разные реальные процессы путём их компьютерного моделирования ( метод Монте-Карло ) .
Во 2-й половине XX века в важное направление математической лингвистики оформилось применение методов теории вероятностей и математической статистики к изучению лингвистических явлений. Многочисленные исследования, основанные на применении таких методов, включали: получение вероятностно-информационных оценок нормы языка; анализ распределения синтактической информации в пределах словоформы , контекстной обусловленности и избыточности текстов , взаимодействия случайных и детерминированных процессов в речи ; разработку адекватных методик лингвистического эксперимента; выявление статистических характеристик лингвистических вариационных рядов и др.
К моменту создания теории вероятностей основой математики были два класса объектов — числа и геометрические фигуры. Для теории вероятностей потребовалось добавить в этот список совершенно особый объект: случайное событие , а также тесно связанные с ним понятия (вероятность, случайная величина и др.). Своеобразие новой науки проявлялось и в том, что её утверждения носили не безусловный характер, как ранее было принято в математике, а предположительно-вероятностный.
По мере развития теории вероятностей не прекращались споры о том, можно ли считать идеализированное событие математическим понятием (и тогда теория вероятностей есть часть математики) или же это факт, наблюдаемый в опыте (и тогда теорию вероятностей следует отнести к естественным наукам). Разные учёные высказывали самые разные мнения на этот счёт. П. Л. Чебышёв уверенно считал теорию вероятностей математической дисциплиной, задача которой — по известным вероятностям некоторых событий определить неизвестную вероятность исследуемого события. По мнению Давида Гильберта , теория вероятностей родственна механике, то есть представляет собой математизированную «физическую дисциплину» . Август де Морган и его последователь У. С. Джевонс считали базовым понятием « субъективную вероятность », то есть количественную меру нашего понимания предмета исследования, и связывали теорию вероятностей с логикой . Проблемы, связанные с неоднозначной субъективной вероятностью, неоднократно обсуждались, их часто формулируют в виде «вероятностных парадоксов» (см., например, « парадокс трёх узников » или « парадокс мальчика и девочки »). Формализацию субъективной вероятности, совместимую с колмогоровской, предложили Бруно де Финетти (1937) и Леонард Сэвидж (1954).
Ещё Бернулли дал фактически два определения вероятности: как доли «благоприятных случаев» и как статистической частоты; чтобы свести второе понимание к первому, понадобился закон больших чисел . Австрийский математик и механик Рихард фон Мизес предложил обратный подход (1914 год): считать определением вероятности именно предел частоты. Теорию вероятностей Мизес к математике не относил, он считал её опытной наукой, изучающей наблюдаемые факты . Определение Мизеса и изложенная им аксиоматика подверглись критике за бессодержательность, поскольку не существует средств для выяснения, имеет ли частота заданного события предел . Обсуждение концепции Мизеса иногда продолжается и в наши дни . Были и другие попытки обоснования — Джон Мейнард Кейнс (1921) и Гарольд Джеффрис (1939) предложили понимать вероятность утверждения как «степень правдоподобия» этого утверждения, этот подход также время от времени упоминается в обсуждении вопроса .

В начале XX века школа Д. Гильберта поставила такие классические разделы математики, как геометрия и анализ, на строгую аксиоматическую основу, появилась аксиоматика и в других разделах математики: теория множеств , математическая логика и др. Назрела необходимость разработать аксиоматику и для теории вероятностей, поскольку старое, полуинтуитивное и неформальное обоснование Бернулли и Лапласа давно устарело. Первый вариант такой аксиоматики дал советский математик С. Н. Бернштейн в своём курсе «Теория вероятностей» (1927 год). Общепризнанным в науке стал вариант А. Н. Колмогорова , опубликованный в 1929—1933 годах и основанный на идеях теории меры . Во второй половине XX века Альфред Реньи и А. Н. Колмогоров исследовали возможность дать обоснование теории вероятностей на базе теории информации . В наши дни «сложилось чёткое понимание того, что теория вероятностей является подлинно математической наукой, имеющей вместе с тем самые тесные и непосредственные связи с широким спектром наук о природе, а также с техническими и социально-экономическими дисциплинами» .
Несмотря на доказанную практикой эффективность вероятностных методов, роль случайности в природе, причина и границы статистической устойчивости остаются предметом дискуссий . «За 200 лет, прошедших со времен Лапласа и Гаусса, наука не добилась продвижения в фундаментальном вопросе — когда возникает статистическая устойчивость» .