История математики в Армении
- 1 year ago
- 0
- 0

История тригонометрии как науки о соотношениях между углами и сторонами треугольника и других геометрических фигур охватывает более двух тысячелетий. Большинство таких соотношений нельзя выразить с помощью обычных алгебраических операций , и поэтому понадобилось ввести особые тригонометрические функции , первоначально оформлявшиеся в виде числовых таблиц.
Историки полагают, что тригонометрию создали древние астрономы ; немного позднее её стали использовать в геодезии и архитектуре . Со временем область применения тригонометрии постоянно расширялась, и в наши дни она включает практически все естественные науки, технику и ряд других областей деятельности . Особенно полезными тригонометрические функции оказались при изучении колебательных процессов ; на них основан также гармонический анализ функций и другие инструменты анализа . Томас Пейн в своей книге « Век Разума » (1794) назвал тригонометрию «душой науки» .

Зачатки тригонометрии можно найти в математических рукописях древнего Египта , Вавилона и древнего Китая . 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей .
От вавилонской математики ведёт начало привычное нам измерение углов градусами, минутами и секундами (введение этих единиц в древнегреческую математику обычно приписывают Гипсиклу , II век до н. э.). Среди известных вавилонянам теорем была, например, такая: вписанный угол , опирающийся на диаметр круга — прямой . Главным достижением этого периода стало соотношение, позже получившее имя теоремы Пифагора ; Ван дер Варден считает, что вавилоняне открыли его между 2000 и 1786 годами до н. э. Вполне возможно, что китайцы открыли его независимо (см. « Математика в девяти книгах »); неясно, знали ли общую формулировку теоремы древние египтяне, но прямоугольный « египетский треугольник » со сторонами 3, 4 и 5 был там хорошо известен и широко использовался .
Общее и логически связное изложение тригонометрических соотношений появилось в древнегреческой геометрии . Греческие математики ещё не выделяли тригонометрию как отдельную науку — для них она была частью астрономии .
Несколько теорем тригонометрического характера содержат «Начала» Евклида (IV век до н. э.). В первой книге «Начал» теоремы 18 и 19 устанавливают, что большей стороне треугольника соответствует больший противолежащий угол — и обратно, большему углу соответствует бо́льшая сторона. Теоремы 20 и 22 формулируют « неравенство треугольника »: из трёх отрезков можно составить треугольник тогда и только тогда, когда длина каждого меньше суммы длин двух других. Теорема 32 доказывает, что сумма углов треугольника равна 180°.
Во второй книге «Начал» теорема 12 представляет собой словесный аналог теоремы косинусов :
В тупоугольных треугольниках квадрат на стороне, стягивающей тупой угол, больше [суммы] квадратов на сторонах, содержащих тупой угол, на дважды взятый прямоугольник, заключённый между одной из сторон при тупом угле, на которую падает перпендикуляр, и отсекаемым этим перпендикуляром снаружи отрезком при тупом угле.
Следующая за ней теорема 13 — вариант теоремы косинусов для остроугольных треугольников. Аналога теоремы синусов у греков не было, это важнейшее открытие было сделано гораздо позднее .
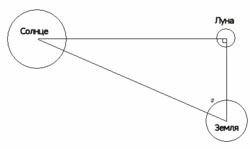
Дальнейшее развитие тригонометрии связано с именем астронома Аристарха Самосского (III век до н. э.). В его трактате «О величинах и расстояниях Солнца и Луны» ставилась задача об определении расстояний до небесных тел; эта задача требовала вычисления отношения сторон прямоугольного треугольника при известном значении одного из углов. Аристарх рассматривал прямоугольный треугольник, образованный Солнцем, Луной и Землёй во время квадратуры . Ему требовалось вычислить величину гипотенузы (расстояние от Земли до Солнца) через катет (расстояние от Земли до Луны) при известном значении прилежащего угла (87°), что эквивалентно вычислению значения . По оценке Аристарха, эта величина лежит в промежутке от 1/20 до 1/18, то есть расстояние до Солнца в 20 раз больше, чем до Луны ; на самом деле Солнце почти в 400 раз дальше, чем Луна, ошибка возникла из-за неточности в измерении угла. Попутно Аристарх доказал неравенство, которое в современных терминах передаётся формулой:
Это же неравенство содержится в «Исчислении песчинок» Архимеда . В трудах Архимеда (III век до н. э.) имеется важная теорема деления хорд, по существу эквивалентная формуле синуса половинного угла :

В течение всего периода развития античной науки главным полем для приложения результатов плоской тригонометрии у греков оставалась астрономия. Помимо задачи о вычислении расстояний, привлечения тригонометрии требовало определение параметров системы эпициклов и/или эксцентров, представляющих движение светила в пространстве. Согласно широко распространённому мнению, эта проблема впервые была сформулирована и решена Гиппархом (середина II века до н. э.) при определении элементов орбит Солнца и Луны; возможно, аналогичными задачами занимались и астрономы более раннего времени. Ему же часто приписывают авторство первых тригонометрических таблиц, не дошедших до нас . Впрочем, согласно некоторым реконструкциям, первые тригонометрические таблицы были составлены ещё в III веке до н. э., возможно, Аполлонием Пергским .
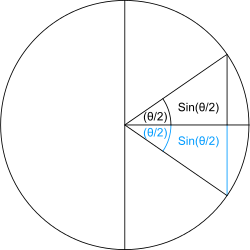
Вместо современной функции синуса Гиппарх и другие древнегреческие математики обычно рассматривали зависимость длины хорды окружности от заданного центрального угла (или, что эквивалентно, от заданной дуги окружности, выраженной в угловой мере). В современной терминологии, длина хорды, стягивающей дугу θ единичной окружности , равна удвоенному синусу центрального угла θ/2. Это соответствие справедливо для любых углов: 0° < θ < 360°. На языке хорд были сформулированы первые открытые греками тригонометрические соотношения . Например, современной формуле:
соответствовала у греков теорема :
где — хорда для центрального угла , — диаметр круга.
При этом радиус круга не считался равным единице, как сейчас. Например, у Гиппарха радиус круга предположительно считался равным R= 3438 единиц — при таком определении длина дуги окружности была равна угловой мере этой дуги, выраженной в минутах: , и это облегчало вычисления. У Птолемея R= 60 единиц. Согласно современным реконструкциям , величины хорд у Гиппарха были протабулированы с интервалом 7°30'. Возможно, в основе вычисления таблицы Гиппарха лежал метод, разработанный Архимедом и восходящий ещё к Аристарху .
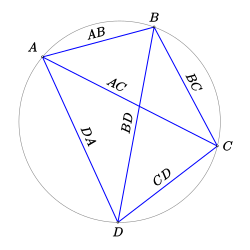
Позднее астроном II века Клавдий Птолемей в « Альмагесте » дополнил результаты Гиппарха. Тринадцать книг «Альмагеста» — самая значимая тригонометрическая работа всей античности. В частности, «Альмагест» содержит обширные пятизначные таблицы хорд для острых и тупых углов, с шагом 30 угловых минут . Для вычисления хорд Птолемей использовал (в главе X) теорему Птолемея (известную, впрочем, ещё Архимеду), которая утверждает: сумма произведений длин противоположных сторон выпуклого вписанного в круг четырёхугольника равна произведению длин его диагоналей. Из этой теоремы нетрудно вывести две формулы для синуса и косинуса суммы углов и ещё две для синуса и косинуса разности углов, однако общая формулировка этих теорем у греков отсутствует .
Основным достижением античной тригонометрической теории стало решение в общем виде задачи «решения треугольников» , то есть нахождения неизвестных элементов треугольника, исходя из трёх заданных его элементов (из которых хотя бы один является стороной) . Впоследствии эта задача и её обобщения стали основной задачей тригонометрии : заданы несколько (обычно три) известных элементов треугольника, требуется найти остальные связанные с ним величины. Первоначально в число элементов треугольника (известных или неизвестных) включали стороны и углы при вершинах, позже к ним добавились медианы , высоты , биссектрисы , радиус вписанной или описанной окружности, положение центра тяжести и т. д. Прикладные тригонометрические задачи отличаются большим разнообразием — например, могут быть заданы измеримые на практике результаты действий над перечисленными величинами (к примеру, сумма углов или отношение длин сторон).
Параллельно с развитием тригонометрии плоскости греки, под влиянием астрономии, далеко продвинули сферическую тригонометрию . В «Началах» Евклида на эту тему имеется только теорема об отношении объёмов шаров разного диаметра, но потребности астрономии и картографии вызвали быстрое развитие сферической тригонометрии и смежных с ней областей — системы небесных координат , теории картографических проекций , технологии астрономических приборов (в частности, была изобретена астролябия ).
Историки не пришли к консенсусу насчёт степени развития у античных греков геометрии небесной сферы . Некоторые исследователи приводят доводы, что эклиптическая или экваториальная система координат использовалась для записи результатов астрономических наблюдений по меньшей мере уже во времена Гиппарха . Возможно, тогда были известны и некоторые теоремы сферической тригонометрии, которые могли использоваться для составления звёздных каталогов и в геодезии .
Первые известные нам труды по «Сферике» (то есть сферической геометрии, с ясным астрономическим уклоном) написали :
Некоторые разобранные в этих сочинениях задачи носят тригонометрический характер, однако из-за слабой разработанности теории авторы ещё применяют обходные пути. Например, задачу «найти время полного восхода (захода) зодиакального созвездия » Гипсикл решает приближённо с помощью многоугольных чисел .

Решающим этапом в развитии теории стала монография «Сферика» в трёх книгах, которую написал Менелай Александрийский (около 100 года н. э.). В первой книге он изложил теоремы о сферических треугольниках , аналогичные теоремам Евклида о плоских треугольниках (см. I книгу «Начал»). Историки считают, что подход Менелая во многом опирается на труды Феодосия , которые у Менелая существенно расширены и приведены в систему. По сообщению Паппа , Менелай первым ввёл понятие сферического треугольника как фигуры, образованной отрезками больших кругов . Менелай доказал теорему, для которой у Евклида нет плоского аналога: два сферических треугольника конгруэнтны (совместимы), если соответствующие углы равны. Другая его теорема утверждает, что сумма углов сферического треугольника всегда больше 180° .
Вторая книга «Сферики» излагает применение сферической геометрии к астрономии. Третья книга содержит важную для практической астрономии теорему Менелая , известную как «правило шести величин» . Две другие открытые Менелаем фундаментальные теоремы впоследствии получили названия «правило четырёх величин» и «правило тангенсов» .
Несколько десятилетий спустя Клавдий Птолемей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике. Среди прочего, описана стереографическая проекция , исследованы несколько практических задач, например: определить высоту и азимут небесного светила по его склонению и часовому углу . С точки зрения тригонометрии, это значит, что надо найти сторону сферического треугольника по другим двум сторонам и противолежащему углу .
Сферической геометрии Птолемей посвятил также XIII главу в первой книге «Альмагеста»; в отличие от Менелая, Птолемей не привёл доказательств многих утверждений, но зато уделил много внимания алгоритмам, пригодным для практических вычислений в астрономии. Опорной конструкцией, вместо плоских хорд, в «Альмагесте» служит «четырёхсторонник Менелая». Для «решения» прямоугольного сферического треугольника, то есть для вычисления его характеристик, Птолемей привёл в словесной записи 4 теоремы; в современных обозначениях они имеют вид (угол прямой) :
Поясним, что в сферической геометрии принято измерять стороны треугольника не линейными единицами, а величиной опирающихся на них центральных углов . В современной сферической тригонометрии приводятся ещё два соотношения:
У Птолемея они отсутствуют, поскольку их нельзя вывести из теоремы Менелая .
В IV веке, после упадка античной науки, центр развития математики переместился в Индию. Сочинения индийских математиков ( сиддханты ) показывают, что их авторы были хорошо знакомы с трудами греческих астрономов и геометров . Чистой геометрией индийцы интересовались мало, но их вклад в прикладную астрономию и расчётные аспекты тригонометрии очень значителен.
В первую очередь индийцы изменили некоторые концепции тригонометрии, приблизив их к современным. Они провели замену античных хорд на синусы (название «синус» восходит к слову «тетива» на санскрите ) в прямоугольном треугольнике . Тем самым в Индии было положено начало тригонометрии как общему учению о соотношениях в треугольнике, хотя, в отличие от греческих хорд, индийский подход ограничивался только функциями острого угла .
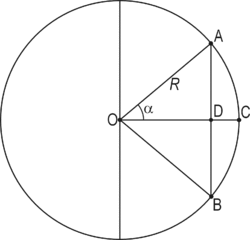
Синус индийцы определяли несколько иначе, чем в современной математике (см. рис. справа): под синусом понималась длина отрезка AD, опирающегося на дугу AC окружности радиуса R= 3438 единиц (как у Гиппарха ). Таким образом, «индийский синус» угла в 3438 раз больше современного синуса и имел размерность длины . Из этого правила были исключения; например, Брахмагупта по неясным причинам принял радиус равным 3270 единиц .
Индийцы первыми ввели в использование косинус . Использовался ещё так называемый обращённый синус, или синус-верзус , равный длине отрезка DC на рисунке справа .
Как и у греков, тригонометрия индийцев развивалась главным образом в связи с её астрономическими приложениями, в основном для использовании в теории движения планет и для изучения небесной сферы. Это свидетельствует о хорошем знании сферической тригонометрии «Альмагеста» и «Аналеммы», однако ни одной их собственной работы, развивающей теорию этого раздела тригонометрии, не обнаружено . Тем не менее в разработке прикладных алгоритмов решения астрономических задач индийцы достигли больших успехов . Например, в «Панча-сиддхантике» Варахамихиры (VII в.) даётся оригинальное решение астрономической задачи, описанной у Птолемея: найти высоту Солнца над горизонтом, если известны широта местности, склонение Солнца и его часовой угол . Автор для решения применяет аналог теоремы косинусов , он же впервые привёл формулу для синуса половинного угла .

Для астрономических расчётов был составлен ряд тригонометрических таблиц. Первые (четырёхзначные) таблицы синусов приведены в древней «Сурья-сиддханте» и у Ариабхаты («Ариабхатия», V век). Таблицы Ариабхаты содержат 24 значения синусов и синус-верзусов с интервалом 3°45' (половина шага таблиц у Гиппарха).
Важный вклад в развитие тригонометрии внес Брахмагупта (VII в.), открывший интерполяционную формулу , которая позволила ему получить значения синуса на основе небольшого количества известных значений этой функции . Кроме того, индийцы знали формулы для кратных углов , для . В «Сурья-сиддханте» и в трудах Брахмагупты при решении задач фактически используется сферический вариант теоремы синусов , однако общая формулировка этой теоремы в Индии так и не появилась . Историки нашли в индийских трудах неявное использование тангенсов , но важность этого понятия была осознана только позже, математиками исламских стран .
В трудах другого выдающегося ученого, Бхаскары II (XII век), приводятся формулы для синуса и косинуса суммы и разности углов:
а также формула для малого приращения синуса:
(при ), соответствующая современному выражению для дифференциала синуса. Опираясь на формулу синуса суммы, Бхаскара опубликовал более точные и подробные, чем у Ариабхаты, тригонометрические таблицы с шагом 1° .
В XI веке мусульмане ( Махмуд Газневи ) захватили и разорили Северную Индию. Культурные центры переместились в Южную Индию, где образуется так называемая « керальская школа астрономии и математики » (по названию современного штата Керала на юге Индии) . В XV—XVI веках математики Кералы в ходе астрономических исследований добились больших успехов в области суммирования бесконечных числовых рядов, в том числе для тригонометрических функций . В анонимном трактате «Каранападдхати» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды , восходящие, вероятно, к основателю этой школы астроному Мадхаве из Сангамаграмы (1-я половина XV века) . Мадхава и его последователь Нилаканта (в трактате « Taнтpacaнrpaха ») приводят также правила разложения арктангенса в бесконечный степенной ряд. В Европе к подобным результатам подошли лишь в XVII—XVIII веках. Так, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 года, а ряд арктангенса был найден Дж. Грегори в 1671 году и Г. В. Лейбницем в 1673 году .
В VIII веке учёные стран Ближнего и Среднего Востока познакомились с трудами древнегреческих и индийских математиков и астрономов. Переводом их на арабский язык занимались такие крупные учёные VIII века, как Ибрахим Ал-Фазари и Якуб ибн Тарик . Далее они и их последователи стали активно комментировать и развивать эти теории. Опорной конструкцией у исламских учёных, как и у индийцев, был синус в треугольнике, или, что то же самое, полухорда в круге .
Их астрономические трактаты, аналогичные индийским сиддхантам, назывались « зиджи »; типичный зидж представлял собой сборник астрономических и тригонометрических таблиц, снабжённый руководством по их использованию и (не всегда) изложением общей теории . Сравнение зиджей периода VIII—XIII веков показывает быструю эволюцию тригонометрических знаний. Предметом особого внимания ученых стран ислама была сферическая тригонометрия, методы которой использовались для решения задач астрономии и геодезии . Среди основных решаемых проблем были следующие .

Самые ранние из сохранившихся трудов принадлежат ал-Хорезми и ал-Марвази (IX век), которые рассмотрели, наряду с известными ещё индийцам синусом и косинусом, новые тригонометрические функции: тангенс , котангенс , секанс и косеканс . Изначально эти функции определялись иначе, чем в современной математике. Так, под котангенсом понималась длина тени от вертикального гномона высотой 12 (иногда 7) единиц; первоначально эти понятия использовались для расчёта солнечных часов . Тангенсом называлась тень от горизонтального гномона. Косекансом и секансом назывались гипотенузы соответствующих прямоугольных треугольников (отрезки AO на рисунке справа) . Лишь в X веке философ и математик ал-Фараби в своих комментариях к «Альмагесту» ввёл независимые от гномоники определения этих четырёх функций, определив их через синус и косинус в тригонометрическом круге птолемеевского радиуса (60 единиц). Основные соотношения между всеми шестью функциями привёл ал-Баттани в том же столетии. Окончательной унификации добился Абу-л-Вафа во второй половине X века, который впервые использовал для определения тригонометрических функций круг единичного радиуса, как это делается в современной математике.
Сабит ибн Курра (IX век) и ал-Баттани (X век) первыми открыли фундаментальную теорему синусов для частного случая прямоугольного сферического треугольника . Для произвольного сферического треугольника доказательство было найдено (разными способами и, вероятно, независимо друг от друга) Абу-л-Вафой, ал-Худжанди и ибн Ираком в конце X века . В другом трактате ибн Ирака сформулирована и доказана теорема синусов для плоского треугольника .
Сферическая теорема косинусов в общем виде сформулирована в странах ислама не была, однако в трудах Сабита ибн Курры, ал-Баттани и других астрономов имеются эквивалентные ей утверждения. Вероятно, поэтому Региомонтан , впервые давший общую формулировку этой важного соотношения (XV век), назвал его «теоремой Альбатегния» (так тогда в Европе называли ал-Баттани) .
Ибн Юнис (X век) открыл преобразование произведения тригонометрических функций в сумму , например:
Формулы преобразования позволяли заменить трудоёмкое умножение на более простое сложение или вычитание. Впоследствии в Европе эти же формулы использовали для противоположной цели — замены сложения и вычитания на умножение, чтобы затем для вычисления результата применить логарифмические таблицы .
Одной из важнейших задач науки того времени являлось составление тригонометрических таблиц с как можно меньшим шагом. В IX веке ал-Хорезми составил таблицы синусов с шагом 1°, его современник Хаббаш аль-Хасиб (ал-Марвази) добавил к ним первые таблицы тангенсов, котангенсов и косекансов (с тем же шагом) . В начале X века ал-Баттани опубликовал таблицы с шагом 30', в конце того же столетия Ибн Юнис составил таблицы с шагом 1' . При составлении таблиц ключевым было вычисление значения . Искусные методы для вычисления этой величины изобрели Ибн Юнис, Абу-л-Вафа , ал-Бируни . Наибольшего успеха добился в XV веке ал-Каши ; в одной из своих работ он подсчитал, что (все знаки верны). В составленных при его участии «Астрономических таблицах» Самаркандской обсерватории Улугбека таблицы синусов вычислены с шестью шестидесятеричными знаками , с шагом 1'. Султан Улугбек лично участвовал в этой работе: он написал специальный трактат о вычислении синуса угла в 1°.

Первым специализированным трактатом по тригонометрии было сочинение среднеазиатского учёного ал-Бируни (X—XI век) «Книга ключей науки астрономии» (995—996 годы). Целый курс тригонометрии содержал главный труд ал-Бируни — «Канон Мас‘уда» (книга III). В дополнение к таблицам синусов (с шагом 15') Ал-Бируни дал таблицы тангенсов (с шагом 1°). Идеологически труды Бируни близки к птолемеевским — на языке хорд он формулирует теоремы о синусе удвоенного и половинного угла, синусе суммы и разности углов . Среди приложений книга Ал-Бируни показывает построение правильного вписанного девятиугольника и приближённое вычисление длины его стороны; этот алгоритм он использует для нахождения . В другом труде, «Геодезия», Бируни сообщил результаты собственных измерений длины земного меридиана , из которых следует оценка радиуса Земли, близкая к истинной (в пересчёте к метрической системе , Бируни получил 6340 км) .
Фундаментальное изложение тригонометрии как самостоятельной науки (как плоской, так и сферической) дал персидский математик и астроном Насир ад-Дин ат-Туси в 1260 году . Его «Трактат о полном четырёхстороннике» содержит практические способы решения типичных задач, в том числе труднейших, решенных самим ат-Туси — например, построение сторон сферического треугольника по заданным трём углам . Приведена теорема тангенсов для сферических треугольников, описано важное понятие полярного треугольника (впервые использованное в XI веке Ибн Ираком и ал-Джайяни ). Сочинение ат-Туси стало широко известно в Европе и существенно повлияло на развитие тригонометрии.
Таким образом, к концу XIII века были открыты базовые теоремы, составляющие содержание тригонометрии:
Из-за отсутствия алгебраической символики все перечисленные теоремы выражались в громоздкой словесной форме, но по существу были полностью эквивалентны современному их пониманию.

После того как арабские трактаты были в XII—XIII веках переведены на латынь, многие идеи индийских и персидских математиков стали достоянием европейской науки. По всей видимости, первое знакомство европейцев с тригонометрией состоялось благодаря зиджу ал-Хорезми , два перевода которого были выполнены в XII веке. Первоначально сведения о тригонометрии (правила её использования, таблицы некоторых тригонометрических функций) приводились в сочинениях по астрономии, однако в сочинении Фибоначчи «Практика геометрии», написанном около 1220 года, тригонометрия излагается как часть геометрии. Первым европейским сочинением, целиком посвященным тригонометрии, часто называют «Четыре трактата о прямых и обращенных хордах» английского астронома Ричарда Уоллингфордского (около 1320 г.). Книга содержит доказательство ряда тригонометрических тождеств и оригинальный метод вычисления синусов. Примерно в те же годы был написан трактат еврейского математика Леви бен Гершома (Герсонида) «О синусах, хордах и дугах», переведённый на латинский язык в 1342 году . Книга содержит доказательство теоремы синусов и пятизначные таблицы синусов . Тригонометрия затрагивается в «Теоретической геометрии» английского математика Томаса Брадвардина (написана в первой половине XIV в., опубликована в 1495 году). Тригонометрические таблицы, чаще переводные с арабского, но иногда и оригинальные, содержатся в сочинениях ряда других авторов XIV—XV веков. Тогда же тригонометрия заняла место среди университетских курсов.
Крупным достижением стала монография Региомонтана «Пять книг о треугольниках всех видов» (опубл. 1462—1464), в которой были сведены все известные к этому моменту знания по плоской и сферической тригонометрии и приложены семизначные таблицы синусов (с шагом 1') и тангенсов (с шагом 1°). Немаловажно и то, что в таблицах Региомонтана, в нарушение астрономической традиции, впервые использовалась десятичная система (а не архаичная шестидесятеричная ). Радиус тригонометрического круга Региомонтан принял равным , чтобы табличные значения были представлены целыми числами (десятичные дроби вошли в обиход несколько позднее, причём мощным стимулом к их применению стали именно тригонометрические вычисления ).
По сравнению с трактатом ат-Туси сочинение Региомонтана существенно полнее, оно содержит ряд новых задач, решённых оригинальными методами. Например, показывается, как построить треугольник, если известны одна его сторона, длина опущенной на неё высоты и противолежащий угол .

Развитие тригонометрии в Новое время стало чрезвычайно важным не только для астрономии и астрологии, но и для других приложений, в первую очередь артиллерии , оптики и навигации при дальних морских путешествиях. Поэтому после XVI века этой темой занимались многие выдающиеся учёные, в том числе Николай Коперник , Иоганн Кеплер , Франсуа Виет . Коперник посвятил тригонометрии две главы в своём трактате « О вращении небесных сфер » (1543). Вскоре (1551) появились 15-значные тригонометрические таблицы Ретика , ученика Коперника, с шагом 10" . Кеплер опубликовал труд «Оптическая часть астрономии» (1604).
Потребность в сложных тригонометрических расчётах вызвала в начале XVII века открытие логарифмов , причём первые логарифмические таблицы Джона Непера содержали только логарифмы тригонометрических функций. Среди других открытий Непера — эффективный алгоритм решения сферических треугольников , получивший название « формулы аналогии Непера » .
Термин «тригонометрия» как название математической дисциплины ввёл в употребление немецкий математик Б. Питискус , опубликовавший в 1595 году книгу «Тригонометрия, или краткий и ясный трактат о решении треугольников » ( лат. Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuus ). К концу XVII века появились современные названия тригонометрических функций. Термин «синус» впервые употребил около 1145 года английский математик и арабист Роберт Честерский . Региомонтан в своей книге назвал косинус «синусом дополнения» ( лат. sinus complementi ), поскольку ; его последователи в XVII веке сократили это обозначение до co-sinus (Эдмунд Гунтер) , а позднее — до cos ( Уильям Отред ). Названия тангенса и секанса предложил в 1583 году датский математик Томас Финке , а упомянутый выше Эдмунд Гунтер ввёл названия котангенса и косеканса . Термин «тригонометрические функции» впервые употребил в своей «Аналитической тригонометрии» (1770) Георг Симон Клюгель .

Томас Финке предложил оригинальное решение геодезической задачи: найти углы треугольника, если известна их сумма и отношение противолежащих сторон . Для решения Финке использовал формулу Региомонтана (см. рисунок) :
Виет в первой части своего «Математического канона» (1579) поместил разнообразные таблицы, в том числе тригонометрические, а во второй части дал обстоятельное и систематическое, хотя и без доказательств, изложение плоской и сферической тригонометрии. В 1593 году Виет подготовил расширенное издание этого капитального труда. «Несомненно, что самый интерес его к алгебре первоначально был вызван возможностью приложений к тригонометрии и астрономии» . Другой важной заслугой Виета стало применение в тригонометрии разработанной им общей алгебраической символики; если ранее решение задачи понималось как геометрическое построение, то начиная с работ Виета приоритет начинает переходить к алгебраическим вычислениям . Появление символики позволило записать в компактном и общем виде тригонометрические тождества — например, формулы для кратных углов :
Надо оговориться, что сам Виет ещё дал эти формулы частично в словесном описании, но при этом ясно указал на связь коэффициентов формул с биномиальными коэффициентами и привёл таблицу их значений для небольших значений .
Из других достижений Виета : в работе «Дополнение к геометрии» Виет указал тригонометрический способ решения кубического уравнения для самого трудного в тот период — неприводимого — случая (стандартная формула требует умения работать с корнями из комплексных чисел ). Виет дал первое в истории бесконечное произведение:

Кроме артиллерии и навигации, тригонометрия быстро развивалась и в таких классических областях её применения, как геодезия . Широкое применение тангенсов объяснялось, в частности, простотой измерения с их помощью высоты горы или здания (см. рисунок):
В 1615 году Снеллиус нашёл решение «задачи Снеллиуса-Потенота» : найти точку, из которой стороны данного (плоского) треугольника видны под заданными углами. Он открыл закон преломления света : для заданных исходной и преломляющей среды отношение синусов угла падения и угла преломления постоянно. Тем самым Снеллиус открыл дорогу новым применениям тригонометрических функций в оптике, а изобретение в эти же годы первых телескопов придало этому открытию особую важность.

Первый график синусоиды появился в книге Альбрехта Дюрера «Руководство к измерению циркулем и линейкой» ( нем. Underweysung der Messung mit dem Zirkel und Richtscheyt , 1525 год) . В 1630-х годах Жиль Роберваль , в ходе своих исследований циклоиды , независимо вычертил синусоиду , он же опубликовал формулу тангенса двойного угла . Джон Валлис в своей «Механике» (1670), опередив своё время, правильно указал знаки синуса во всех квадрантах и указал, что у синусоиды бесконечно много «оборотов». График тангенса для первого квадранта впервые начертил Джеймс Грегори (1668) .
Во второй половине XVII века началось стремительное развитие общей теории квадратур (то есть вычисления площади), завершившееся появлением в конце века математического анализа . Для тригонометрических функций важные результаты в начале этого периода получил Блез Паскаль (опубликованы в его книге «Письма А. Деттонвилля о некоторых его геометрических открытиях», 1659 год). В современной терминологии, Паскаль вычислил интегралы от натуральных степеней синуса и косинуса и некоторые связанные с ними , а также отметил, что . Работы в области тригонометрии проводили такие крупные математики XVII века, как Отред , Гюйгенс , Озанам , Валлис . Заметным процессом во второй половине XVII века стала постепенная алгебраизация тригонометрии, совершенствование и упрощение её символики (хотя до Эйлера символика была всё же гораздо более громоздка, чем современная) .
После открытия математического анализа сначала Джеймс Грегори , а затем Исаак Ньютон получили разложение тригонометрических функций (а также обратных к ним ) в бесконечные ряды . Ньютон посвятил проблемам геометрии и тригонометрии 10 задач в своей книге « Универсальная арифметика » . Например, в задаче X требуется «решить треугольник» , если известны одна его сторона, противолежащий угол и сумма двух других сторон. Предложенный Ньютоном метод решения представляет собой одну из формул Мольвейде .
Лейбниц строго доказал, что не может быть, вообще говоря, алгебраически выражен через , то есть, в современной терминологии, тригонометрические функции трансцендентны .
Важными открытиями в начале XVIII века стали:
В 1706 году швейцарский математик Якоб Герман опубликовал формулы для тангенса суммы и тангенса кратных углов, а Иоганн Ламберт в 1765 году нашёл чрезвычайно полезные формулы , выражающие разные тригонометрические функции через тангенс половинного угла . Исследуя гиперболические функции (1761), Ламберт показал, что их свойства аналогичны свойствам тригонометрических; причину этого ещё в 1707 году обнаружил Муавр : при замене вещественного аргумента на мнимый круг переходит в гиперболу , а тригонометрические функции — в соответствующие гиперболические .
Немецкий математик в книге «Анализ треугольников» (1746) опубликовал в современной записи обе формулы Мольвейде .
В книге «Полигонометрия» (1789) Симон Люилье обобщил тригонометрические соотношения для треугольников, дав их аналоги для произвольных многоугольников, включая пространственные. В работах на эту тему Люилье привёл основную теорему полигонометрии : площадь каждой грани многогранника равна сумме произведений площадей остальных граней на косинусы углов, образуемых ими с первой гранью . Он рассмотрел способы «решения многоугольников» с сторонами при различных постановках задачи: заданы сторона и угла, или все углы и стороны, или все стороны и угла .
В 1798 году Лежандр доказал, что если размеры сферического треугольника малы по сравнению с радиусом сферы, то при решении тригонометрических задач можно применять формулы плоской тригонометрии, вычтя при этом из каждого угла треть сферического избытка .
Манера обозначать обратные тригонометрические функции с помощью приставки arc (от лат. arcus — дуга) появилась у австрийского математика Карла Шерфера ( Karl Scherffer , 1716—1783) и закрепилась благодаря Лагранжу . Имелось в виду, что, например, обычный синус позволяет по дуге окружности найти стягивающую её хорду, а обратная функция решает противоположную задачу. Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: , но они не прижились .

Современный вид тригонометрии придал Леонард Эйлер . В трактате «Введение в анализ бесконечных» (1748) Эйлер дал определение тригонометрических функций, эквивалентное современному , и соответственно определил обратные функции . Если его предшественники понимали синус и прочие понятия геометрически, то есть как линии в круге или треугольнике, то после работ Эйлера и т. д. стали рассматриваться как безразмерные аналитические функции действительного и комплексного переменного. Для комплексного случая он установил связь тригонометрических функций с показательной функцией ( формула Эйлера ). Подход Эйлера с этих пор стал общепризнанным и вошёл в учебники.
Эйлер рассматривал как допустимые отрицательные углы и углы, большие 360°, что позволило определить тригонометрические функции на всей вещественной числовой прямой , а затем продолжить их на комплексную плоскость . Когда встал вопрос о распространении тригонометрических функций на тупые углы, знаки этих функций до Эйлера нередко выбирались ошибочно; многие математики считали, например, косинус и тангенс тупого угла положительными . Эйлер определил эти знаки для углов в разных координатных квадрантах, исходя из формул приведения .
Эйлер впервые представил разложение тригонометрических функций в бесконечные произведения (1734), откуда вывел ряды для их логарифмов .
В других трудах, в первую очередь «Основания сферической тригонометрии, выведенные из метода максимумов и минимумов» (1753) и «Всеобщая сферическая тригонометрия, кратко и ясно выведенная из первых оснований» (1779), Эйлер впервые дал полное систематическое изложение сферической тригонометрии на аналитическом основании , причём многие крупные результаты принадлежат самому Эйлеру.
В середине XVIII века разгорелся важнейший по своим последствиям «спор о струне» . Эйлер в полемике с Даламбером предложил более общее определение функции, чем принималось ранее; в частности, функция может быть задана тригонометрическим рядом . В своих трудах Эйлер использовал несколько представлений алгебраических функций в виде ряда из кратных аргументов тригонометрических функций, например :
Общей теорией тригонометрических рядов Эйлер не занимался и сходимость полученных рядов не исследовал, но получил несколько важных результатов. В частности, он вывел разложения целых степеней синуса и косинуса .
В России первые сведения о тригонометрии были опубликованы в сборнике «Таблицы логарифмов, синусов и тангенсов к изучению мудролюбивых тщателей», опубликованном при участии Л. Ф. Магницкого в 1703 году . В 1714 году появилось содержательное руководство «Геометрия практика», первый русский учебник по тригонометрии, ориентированный на прикладные задачи артиллерии, навигации и геодезии . Завершением периода освоения тригонометрических знаний в России можно считать фундаментальный учебник академика М. Е. Головина (ученика Эйлера) «Плоская и сферическая тригонометрия с алгебраическими доказательствами» (1789).
В конце XVIII века в Петербурге возникла авторитетная тригонометрическая школа ( А. И. Лексель , Н. И. Фусс , Ф. И. Шуберт ), которая внесла большой вклад в плоскую и сферическую тригонометрию .
В начале XIX века Н. И. Лобачевский добавил к плоской и сферической тригонометрии третий раздел — гиперболическую (для геометрии Лобачевского , первую работу в этой области опубликовал Ф. А. Тауринус в 1826 году). Лобачевский показал, что формулы сферической тригонометрии переходят в формулы гиперболической тригонометрии при замене длин сторон треугольника a, b, c на мнимые величины: ai, bi, ci — или, что эквивалентно, при замене тригонометрических функций на соответствующие гиперболические .
В XIX—XX веках бурное развитие получили теория тригонометрических рядов и связанные с ней области математики: гармонический анализ , теория случайных процессов , кодирование аудио и видеоинформации и другие. Ещё Даниил Бернулли высказал убеждение, что любую (непрерывную) функцию на заданном промежутке можно представить тригонометрическим рядом . Дискуссии продолжались до 1807 года, когда Фурье опубликовал теорию представления произвольных кусочно-аналитических функций тригонометрическими рядами (окончательный вариант содержится в его «Аналитической теории тепла», 1822) . Для разложения функции в ряд:
Фурье привёл интегральные формулы расчёта коэффициентов :
Изложение Фурье не было строгим в современном понимании, но уже содержало исследование сходимости большинства полученных им рядов. Для функций, заданных на всей числовой прямой и не являющихся периодическими, Фурье предложил разложение в интеграл Фурье .
Универсальность и эффективность методов анализа Фурье произвели большое впечатление на научный мир. Если ранее тригонометрические ряды использовались в математической физике преимущественно для изучения периодических процессов (колебания струны, небесная механика , движение маятника и т. п.), то в труде Фурье исследовались процессы совсем иного рода (теплопередача), и тригонометрические ряды помогли получить ценные практические результаты. С этого момента тригонометрические ряды и интегралы стали мощным инструментом анализа разнообразных функций. Результаты Фурье продолжили и углубили Пуассон и Коши , вопрос сходимости рядов детально исследовали Дирихле и другие математики . Риман в своей диссертации исследовал произвольные тригонометрические ряды, не обязательно связанные с разложением какой-либо функции (1853), сформулировал для них «принцип локализации». Вопрос о представимости произвольной измеримой и конечной почти всюду функции тригонометрическим рядом (который не обязательно совпадает с её рядом Фурье) был решён в 1941 году теоремой Меньшова .
Исследуя множества особых точек для тригонометрических рядов, Георг Кантор разработал фундаментальную для всей математики теорию множеств . Огромное влияние теория тригонометрических рядов оказала на развитие комплексного анализа , математической физики , электроники и многих других разделов науки . Теория функций вещественного переменного , теория меры и интеграл Лебега появились и далее развивались в тесной связи с теорией тригонометрических рядов . Важные практические применения имеет приближение функций конечными тригонометрическими полиномами (используемое также для интерполирования ).
В XVIII—XIX веках труды по истории математики и астрономии значительное внимание уделяли и истории тригонометрии ( Ж. Э. Монтукла , Ж. Б. Ж. Деламбр , Г. Ганкель , П. Таннери и другие). В 1900 году немецкий историк математики опубликовал первую монографию в двух томах, специально посвящённую истории тригонометрии . В XX веке крупные работы по этой теме опубликовали И. Г. Цейтен , М. Б. Кантор , О. Нейгебауэр , Б. А. Розенфельд , Г. П. Матвиевская и другие.
|
Эта статья победила на конкурсе
статьи года
и была признана статьёй 2012 года русской Википедии.
|