Interested Article - Модель пересекающихся поколений

- 2021-09-11
- 1


Модель пересекающихся (перекрывающихся) поколений ( модель Даймонда , модель Самуэльсона — Даймонда , англ. overlapping generations model ) — модель экзогенного экономического роста в условиях совершенной конкуренции . Внесла вклад в понимание того, каким образом решения индивидов формируют норму сбережений в экономике . В модели отражено изменение потребительского поведения индивида по мере взросления. Вместе с тем, в модели отрицаются альтруистические связи между поколениями, и она не даёт удовлетворительного объяснения межстрановым различиям в уровне дохода на душу населения. Разработана Питером Даймондом с использованием идей Пола Самуэльсона в 1965 году.
История создания
В первых моделях экономического роста ( модель Солоу , модель Харрода — Домара ) использовались экзогенно задаваемые параметры «норма сбережений » и «темп научно-технического прогресса », от которых, в конечном итоге, и зависели темпы роста. Исследователи же хотели получить обоснование темпов экономического роста внутренними (эндогенными) факторами, поскольку модели с заданной нормой сбережений имели ряд недостатков. Они не объясняли устойчивые различия в уровнях и темпах роста между развивающимися и развитыми странами. В модели Рамсея — Касса — Купманса был преодолён недостаток экзогенности нормы сбережений. Однако она сохранила другой недостаток ранних моделей — в ней рассматривается бесконечно живущий индивид (или домохозяйство) в качестве вечного потребителя . Но по мере взросления характер потребительского поведения меняется. Если в молодом возрасте индивид работает и делает сбережения, то в старости он эти сбережения тратит . Именно на это будущий лауреат Нобелевской премии по экономике Пол Самуэльсон обратил более пристальное внимание. В декабре 1958 года он опубликовал работу «Моделирование процентной ставки на основе соотношения потребления и кредитования при наличии или отсутствии социальной концепции денег», в которой была представлена простая модель экономики на основе идей Ойген фон Бём-Баверка о причинах существования процентного дохода на капитал , где были выделены три периода жизни индивидуума и соответствующее им потребление (в первых двух он работает, в третьем — выходит на пенсию) . В декабре 1965 года Питер Даймонд , также будущий лауреат Нобелевской премии по экономике, опубликовал работу «Национальный долг в неоклассической модели роста» в журнале , в которой он развил идеи Самуэльсона с учётом выводов модели Солоу и модели Рамсея — Касса — Купманса и представил модель пересекающихся поколений , также известную как модель Даймонда , модель Самуэльсона — Даймонда .
Описание модели
Базовые предпосылки модели
В модели рассматривается закрытая экономика . Фирмы максимизируют свою прибыль, а потребители — полезность своих трат. Фирмы функционируют в условиях совершенной конкуренции . Производится только один продукт , используемый как для потребления , так и для производственных нужд (учитывается как инвестиции ) . Темпы технологического прогресса , роста населения и норма выбытия оборудования (капитала) — постоянны и задаются экзогенно . Индивидуумы живут два периода: в первом они работают, потребляют и сберегают, во втором — только потребляют, тратя накопленные в первом периоде сбережения (выходят на пенсию). Альтруистические связи между поколениями отсутствуют: молодые не помогают старикам и не получают наследство. Время изменяется дискретно . Один период в модели соответствует смене поколений, то есть в реальном выражении эквивалентен примерно 25—30 годам .
Закрытость экономики означает, что произведённый продукт тратится только на сбережение и потребление, экспорт/импорт отсутствуют, инвестиции равны сбережениям: , .
Производственная функция удовлетворяет неоклассическим предпосылкам :
- технологический прогресс увеличивает производительность труда (нейтрален по Харроду ): .
- в производственной функции используются труд и капитал , она обладает постоянной отдачей от масштаба: .
- предельная производительность факторов положительная и убывающая: .
- производственная функция удовлетворяет условиям Инады , а именно, если запас одного из факторов бесконечно мал, то его предельная производительность бесконечно велика, если же запас одного из факторов бесконечно велик, то его предельная производительность бесконечно мала: .
- для производства необходим каждый фактор: .
Население растёт с постоянным темпом : . В каждом периоде живёт молодых и пожилых индивидов. Совокупное потребление равно :
- ,
- где — потребление работающего поколения, — потребление вышедшего на пенсию поколения.
Молодой индивид предлагает одну единицу труда ( предложение труда неэластично ) и получает натуральную заработную плату (неким количеством единственного товара, деньги отсутствуют). Каждый индивид выбирает и разделяет полученное между потреблением в молодости или сбережением и потреблением в старости, максимизируя межвременную полезность своих трат, которая описывается следующей функцией :
- ,
- где — эластичность замещения по времени, , , — коэффициент межвременного предпочтения потребителя, , .
Функция удовлетворяет условиям и условиям Инады (при потреблении, стремящемся к нулю, предельная полезность стремится к бесконечности; при потреблении, стремящемся к бесконечности, предельная полезность стремится к нулю): .
Вначале весь капитал находится у пожилых, они его полностью тратят в течение первого периода. Сбережения равны инвестициям, которые делает молодое поколение. Инвестиции в свою очередь равны капиталу в следующем периоде :
- ,
- где — сбережения в расчёте на одного работника.
Для поиска решения модели используются удельные показатели: выпуск на единицу эффективного труда , капитал на единицу эффективного труда .
Задача потребителя
Потребитель максимизирует межвременную полезность своих трат. Поскольку, согласно модели, индивид работает только в молодости (первом периоде), межвременное бюджетное ограничение потребителя соответствует формуле :
- .
Таким образом, задача потребителя имеет следующий вид:
- при условии:
- ,
- где — реальная заработная плата в периоде .
Для решения этой задачи составляется функция Лагранжа и находится её максимум .
- .
Условия максимума:
Результатом решения этой системы уравнений является норма сбережений для периода :
- .
Задача фирмы
Фирма максимизирует свою прибыль . Выпуск фирмы описывается неоклассической производственной функцией :
- , где .
Задача фирмы выглядит следующим образом:
В условиях совершенной конкуренции решение задачи фирмы приводит к тому, что плата за труд ( заработная плата ) и плата за капитал ( процентная ставка ) равны соответствующим предельным производительностям :
- ,
- .
Общее экономическое равновесие


По предпосылкам модели: . Откуда с учётом решения задач потребителя и фирмы, получаем :
- .
Поскольку входит как в правую, так и в левую части уравнения, найти явные решения этого уравнения можно только введя дополнительные предпосылки. При условии, что потребление в первом периоде и потребление во втором периоде являются совершенными заменителями, то равновесие существует. Если при этом сбережения монотонно возрастают по процентной ставке ( ), то это равновесие является единственным.
Если обозначить , где — сбережения в расчёте на единицу труда с постоянной эффективностью в периоде , то уравнение примет вид :
- .
Откуда можно выразить динамику капиталовооружённости :
- .
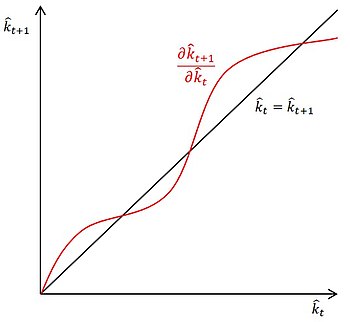
В результате может получиться два варианта фазовой плоскости (см. иллюстрации). В первом варианте кривая выходит из начала координат под углом более чем 45° (выше линии ), и в модели будет нечётное число равновесных состояний (пересечения и ), из которых пересечения, по порядку идущие нечётными от начала координат (первое, третье, пятое и т. д.), будут устойчивыми равновесиями, а идущие чётными (второе, четвёртое и т. д.) — неустойчивыми. Во втором варианте кривая выходит из начала координат под углом менее чем 45° (ниже линии ), и в модели будет чётное число равновесных состояний, из которых пересечения, идущие чётными от начала координат (второе, четвёртое и т. д.), будут устойчивыми равновесиями, а идущие нечётными (первое, третье и т. д.) — неустойчивыми .
Равновесие для производственной функции Кобба-Дугласа и логарифмической функции полезности
Наглядно достижение равновесия можно продемонстрировать в случае логарифмической функции полезности и производственной функции Кобба-Дугласа . В этом случае , а полезность трат для индивида описывается функцией :
- .
Выпуск описывается следующей функцией:
- .
Тогда, норма сбережений равна: , а устойчивый уровень капиталовооружённости (в данном случае существует только одно равновесное состояние) равен : .
Процесс достижения равновесия на фазовой плоскости для рассматриваемого случая показан на иллюстрации.
Устойчивый уровень выпуска на единицу труда с постоянной эффективностью в этом случае составляет:
- .
Как и в моделях Солоу и Рамсея — Касса — Купманса , потребление максимально в том случае, если . Таким образом, в модели возможна динамическая неэффективность (избыточное накопление капитала), в том случае, если :
- .
Конвергенция
Модель предполагает наличие условной конвергенции , то есть, что страны с малым уровнем капиталовооружённости будут расти более высокими темпами, чем страны с большим уровнем капиталовооружённости, при условии, что устойчивое состояние у них одинаково. Частный случай с производственной функцией Кобба — Дугласа и логарифмической полезностью позволяет оценить, насколько быстро она происходит. Скорость приближения к устойчивому состоянию можно оценить при помощи линейной аппроксимации в зависимости от посредством разложения в ряд Тейлора :
- .
Если обозначить производную в точке равновесия , то путем рекуррентных постановок получается следующее уравнение приближения к равновесному состоянию:
- .
Для рассматриваемого случая, , потому:
- .
Таким образом, в рассматриваемом случае скорость конвергенции напрямую зависит от — доли дохода на капитал в общем доходе. Чем меньше доля дохода на капитал, тем быстрее происходит движение к равновесному состоянию, и тем быстрее бедные страны догоняют богатые .
Фискальная политика в модели

Модель позволяет оценить влияние фискальной политики на равновесие. В рамках модели, увеличение налогов и государственных расходов приводит к равновесию с меньшим уровнем капиталовооружённости, выпуска и потребления. Влияние бюджетно-налоговой политики показано на диаграмме. Кривая сдвигается вниз на величину — налогов (государственных расходов) на единицу эффективного труда, величина налогов предполагается равной величине государственных расходов, которые не влияют на полезность индивидов и будущий выпуск. Равновесие сдвигается из точки (устойчивое равновесие) в точку (устойчивое равновесие), и устанавливается на более низком уровне капиталовооружённости и потребления. Появившаяся третья равновесная точка является неустойчивым равновесием. Равенство Рикардо — Барро не выполняется . Таким образом, в модели государственные расходы вытесняют как потребление, так и инвестиции .
Преимущества, недостатки и дальнейшее развитие модели
Одним из существенных недостатков модели является полное отрицание альтруистических связей между поколениями . Чтобы преодолеть этот недостаток, Джеймс Андреони , а также Роберт Барро и Хавьер Сала-и-Мартин предложили ввести в функцию полезности трат каждого индивида полезность трат его детей с некоторым коэффициентом . В этом случае модель превращается в дискретный аналог модели Рамсея — Касса — Купманса для случая когда . Динамическая неэффективность становится невозможной, а последствия бюджетно-налоговой политики отвечают равенству Рикардо — Барро . Однако в этом случае модель приобретает и недостатки модели Рамсея — Касса — Купманса: утрачивается возможность несовершенства рынка (динамической неэффективности), а значит, модель перестает объяснять причины, приводящие к неоптимальному по Парето равновесию в экономике .
Пол Самуэльсон использовал данную модель для исследования влияния распределительной пенсионной системы на общее экономическое равновесие. В работе показано, что, если в экономике установилось динамически неэффективное равновесие с избыточным накоплением капитала, то распределительная пенсионная система позволяет перейти к более оптимальному распределению ресурсов с более высоким потреблением . Если же используется накопительная пенсионная система, то экономическое равновесие остается прежним .
Модификация модели с непрерывным временем, в которой жизнь индивида не делится на периоды молодости и старости, однако индивид может умереть в любой момент с некоторой вероятностью, была разработана Менахемом Яари и Оливье Бланшаром . Из-за того, что в этой модификации вероятность смерти индивида не меняется с возрастом, она получила название «модель вечной молодости» . В ней существует единственное равновесное значение капиталовооружённости, которое при этом устойчиво, и так же, как и в основном варианте, присутствует возможность избыточного накопления в точке равновесия .
В целом, модель пересекающихся поколений более реалистично описывает общее экономическое равновесие и процесс его достижения, чем модели Солоу или Рамсея — Касса — Купманса . Преимуществом модели является возможность динамической неэффективности, однако в модели она связана с избыточным накоплением капитала, которое не является типичной проблемой развивающихся стран, напротив, характеризующихся недостаточным накоплением капитала . К тому же, модель предполагает наличие условной конвергенции, что означает, что бедные страны должны расти быстрее богатых при условии схожести структурных параметров, но в реальности этого не происходит, как показали, например, исследования Р. Холла и Ч. Джонса , Дж. Де Лонга , П. Ромера . Также, как и в моделях Солоу и Рамсея — Касса — Купманса, научно-технический прогресс в модели пересекающихся поколений не является следствием принятия решений экономическими агентами, а задаётся экзогенно. Потому, при всех своих достоинствах, модель не даёт ответа на вопрос, почему одни страны богатые, а другие — бедные, и почему вторые не могут догнать первых .
Примечания
- ↑ , с. 501.
- ↑ , с. 252.
- .
- ↑ , с. 252.
- , с. 110.
- ↑ .
- , с. 252—256.
- , с. 501—505.
- ↑ , с. 264.
- , с. 187.
- , с. 36—47.
- , с. 256.
- , с. 505.
- , с. 509.
- ↑ , с. 255.
- , с. 91.
- ↑ , с. 254.
- ↑ , с. 506.
- ↑ , с. 257.
- ↑ , с. 258.
- , с. 260.
- ↑ , с. 262.
- , с. 513.
- , с. 265.
- , с. 263.
- ↑ , с. 271.
- , с. 267.
- , с. 268.
- .
- .
- , с. 522.
- , с. 520.
- .
- .
- , с. 544.
- , с. 539.
- ↑ , с. 542.
- .
- .
- .
Литература
- Аджемоглу Д. Введение в теорию современного экономического роста: в 2 кн. Книга 1 = Introduction to Modern Economic Growth (2009). — М. : Издательский дом «Дело» РАНХиГС , 2018. — 928 с. — ISBN 978-5-7749-1262-9 .
- Барро Р. Д. , Сала-и-Мартин Х. . — М. : Бином. Лаборатория знаний, 2010. — 824 с. — ISBN 978-5-94774-790-4 .
- Бланшар О. Ж. , Фишер С. Лекции по макроэкономике = Lectures on macroeconomics. — М. : Издательский дом «Дело» РАНХиГС , 2014. — 680 с. — ISBN 978-5-7749-0829-5 .
- Ромер Д. Высшая макроэкономика = Advanced Macroeconomics. — М. : Издательский дом ВШЭ, 2014. — 855 с. — ISBN 978-5-7568-0406-2 .
- Туманова Е. А., Шагас Н. Л. Макроэкономика. Элементы продвинутого подхода. — М. : ИНФРА-М, 2004. — 400 с. — ISBN 5-1600-1864-6 .
- // . — 1989. — Vol. 97, № 6 . — P. 1447—1458. — doi : .
- Blanchard O. J. // . — 1985. — Vol. 93, № 2 . — P. 223—247. — doi : .
- De Long J. B. // . — 1988. — Vol. 78, № 5 . — P. 1138—1154.
- Diamond P. A. // . — 1965. — Vol. 55, № 5 . — P. 1126—1150.
- Hall R. E. , Jones C. I. // NBER Working Paper. — 1996. — № 5812 . — doi : .
- Romer P. M. // NBER Working paper. — 1989. — № 3173 . — doi : .
- Samuelson P. A. // . — 1958. — Vol. 66, № 6 . — P. 467—482. — doi : .
- Samuelson P. A. // . — 1975. — Vol. 16, № 3 . — P. 539—544. — doi : .
- Yaari M. E. // . — 1965. — Vol. 32, № 2 . — P. 137—150. — doi : .
- 2021-09-11
- 1


































































![{\displaystyle (1+n)(1+g){\hat {k}}_{t+1}=s{\bigl (}[f'({\hat {k}}_{t+1})-\delta ],[f({\hat {k}}_{1})-{\hat {k}}_{t}f'({\hat {k}}_{t})]{\bigr )}}](/images/004/916/4916694/72.jpg?rand=193068)