Гравитационное поле Земли — поле силы тяжести, обусловленное тяготением Земли и центробежной силой , вызванной её суточным вращением. Характеризуется пространственным распределением силы тяжести и гравитационного потенциала .

Для решения практических задач потенциал земного притяжения (без учёта центробежной силы и влияния других небесных тел) выражается в виде ряда

${\displaystyle V(r,\phi ,\lambda )={\frac {GM}{r}}\left[1+\sum _{n=1}^{\infty }\left({\frac {a}{r}}\right)^{n}\sum _{m=0}^{n}P_{nm}\sin \phi \left(C_{nm}\cos m\lambda +S_{nm}\sin m\lambda \right)\right],}$ где

${\displaystyle r,\phi ,\lambda }$ — полярные координаты, ${\displaystyle G}$ — гравитационная постоянная, ${\displaystyle M}$ — масса Земли, ${\displaystyle GM}$ = 398 603⋅10 ⁹ м ³ ·с ⁻² , ${\displaystyle a}$ — большая полуось Земли.

Ускорение свободного падения

В неинерциальных системах отсчёта ускорение свободного падения численно равно силе тяжести , воздействующей на объект единичной массы.

Ускорение свободного падения на поверхности Земли g (обычно произносится как «Же» ) варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах . Стандартное («нормальное») значение, принятое при построении систем единиц , составляет g = 9,80665 м/с² . (англ.) ( g было определено как «среднее» в каком-то смысле на всей Земле, оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря . В приблизительных расчётах его обычно принимают равным 9,81; 9,8 или 10 м/с².

В СМИ и научно-популярной литературе g нередко используется как внесистемная единица силы тяжести, применяемая, например, для оценки величины перегрузок при тренировках лётчиков и космонавтов , а также силы тяготения на других небесных телах (см. раздел Сравнение силы тяготения на Земле с другими небесными телами ).

Получение значения g из закона всемирного тяготения

Согласно закону всемирного тяготения , сила земной гравитации, действующая на тело, определяется формулой

${\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}=\left(G{\frac {m_{1}}{r^{2}}}\right)m_{2}}$ ,

где r — расстояние между центром Земли и телом (см. ниже), m ₁ — масса Земли и m ₂ — масса тела.

Кроме того, согласно второму закону Ньютона , F = ma , где m — масса и a — ускорение,

${\displaystyle F=m_{2}g}$

Из сопоставления двух формул видно, что

${\displaystyle g=G{\frac {m_{1}}{r^{2}}}}$

Таким образом, чтобы найти получить значение ускорения силы тяжести g на уровне моря, необходимо в формулу подставить значения гравитационной постоянной G , массы Земли (в килограммах) m ₁ и радиуса Земли (в метрах) r :

${\displaystyle g=G{\frac {m_{1}}{r^{2}}}=(6.67384\times 10^{-11}){\frac {5.9722\times 10^{24}}{(6.371\times 10^{6})^{2}}}=9.8196{\mbox{m}}\cdot {\mbox{s}}^{-2}}$

Следует отметить, что эта формула правомерна для сферического тела при допущении, что вся его масса сосредоточена в его центре. Это позволяет нам использовать величину радиуса Земли для r .

Существуют значительные неопределенности значений r и m ₁ , а также значения гравитационной постоянной G , которую трудно точно измерить.

Если G , g и r известны, то решение обратной задачи позволит получить величину массы Земли.

Гравитационные аномалии

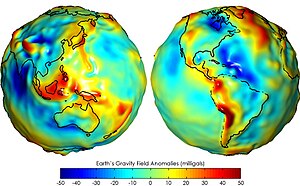
Гравитационные аномалии применительно к геофизике — отклонения величины гравитационного поля от расчётной, вычисленной на основе той или иной математической модели . Гравитационный потенциал земной поверхности, или геоида , обычно описывается на основании математических теорий с использованием гармонических функций . Эти отклонения могут быть вызваны различными факторами, в том числе:

• Земля не является однородной , её плотность различна на разных участках;
• Земля не является идеальной сферой , и в формуле используется среднее значение величины её радиуса;
• Расчётное значение g учитывает только силу тяжести и не учитывает центробежную силу, возникающую за счёт вращения Земли;
• При подъёме тела над поверхностью Земли значение g уменьшается («высотная поправка» (см. ниже), аномалия Бугера );
• На Землю воздействуют гравитационные поля других космических тел, в частности, приливные силы Солнца и Луны.

Высотная поправка

Первая поправка для стандартных математических моделей, так называемая (англ.) ( , позволяет учесть изменение величины g в зависимости от высоты над уровнем моря . Используем значения массы и радиуса Земли:

${\displaystyle r_{\mathrm {Earth} }=6.371\times 10^{6}\,\mathrm {m} }$

${\displaystyle m_{\mathrm {Earth} }=5.9722\times 10^{24}\,\mathrm {kg} }$

Поправочный коэффициент (Δg) может быть получены из соотношения между ускорением силы тяжести g и гравитационной постоянной G :

${\displaystyle g_{0}=G\,m_{\mathrm {Earth} }/r_{\mathrm {Earth} }^{2}=9.8196\,{\frac {\mathrm {m} }{\mathrm {s} ^{2}}}}$ , где:

${\displaystyle G=6.67384\times 10^{-11}\,{\frac {\mathrm {m} ^{3}}{\mathrm {kg} \cdot \mathrm {s} ^{2}}}.}$ .

На высоте h над поверхностью Земли g _h рассчитывается по формуле:

${\displaystyle g_{h}=G\,m_{\mathrm {Earth} }/\left(r_{\mathrm {Earth} }+h\right)^{2}}$

Так, высотная поправка для высоты h может быть выражена:

${\displaystyle \Delta g_{h}=\left[G\,m_{\mathrm {Earth} }/\left(r_{\mathrm {Earth} }+h\right)^{2}\right]-\left[G\,m_{\mathrm {Earth} }/r_{\mathrm {Earth} }^{2}\right]}$ .

Это выражение может быть легко использовано для программирования или включения в таблицу. Упрощая и пренебрегая малыми величинами ( h << r _Earth ), получаем хорошее приближение:

${\displaystyle \Delta g_{h}\approx -\,{\dfrac {G\,m_{\mathrm {Earth} }}{r_{\mathrm {Earth} }^{2}}}\times {\dfrac {2\,h}{r_{\mathrm {Earth} }}}}$ .

Используя приведённые выше численные значения выше, и высоту h в метрах, получим:

${\displaystyle \Delta g_{h}\approx -3.083\times 10^{-6}\,h}$

Учитывая широту местности и высотную поправку, получаем:

${\displaystyle g_{\phi ,h}=9.780327\left(1+0.0053024\sin ^{2}\phi -0.0000058\sin ^{2}2\phi \right)-3.086\times 10^{-6}h}$ ,

где ${\displaystyle \ g_{\phi ,h}}$ — ускорение свободного падения на широте ${\displaystyle \ \phi }$ и высоте h . Это выражение можно также представить в следующем виде:

${\displaystyle g_{\phi ,h}=9.780327\left[\left(1+0.0053024\sin ^{2}\phi -0.0000058\sin ^{2}2\phi \right)-3.155\times 10^{-7}h\right]\,{\frac {\mathrm {m} }{\mathrm {s} ^{2}}}}$ .

Сравнение силы тяготения на Земле с другими небесными телами

В таблице приведены значения величин ускорения свободного падения на поверхности Земли, Солнца , Луны , планет Солнечной системы , ряда спутников и астероидов . Для планет — гигантов под «поверхностью» понимается видимая поверхность, а для Солнца — верхняя граница фотосферы . Данные в таблице не учитывают эффекта центробежной силы от вращения планет и фактически означают значения искомых величин вблизи полюсов планет. Справочно указано время падения объекта на данное небесное тело со 100-метровой высоты и максимальная скорость, достигаемая при этом (сопротивление воздуха не учтено).

Небесное тело	Сила тяжести по сравнению с земной	Ускорение свободного падения на поверхности, м/с 2	Примечания	Время падения со 100-метровой высоты/ Достигаемая при этом скорость
Солнце	27,90	274,1		0,85 сек	843 км/ч
Меркурий	0,3770	3,7		7,4 сек	98 км/ч
Венера	0,905	8,872		4,8 сек	152 км/ч
Земля	1	9,80665		4,5 сек	159 км/ч
Луна	0,1657	1,625		11,1 сек	65 км/ч
Марс	0,3795	3,728		7,3 сек	98 км/ч
Церера	0,028	0,27		26,7 сек	27 км/ч
Юпитер	2,640	25,93		2,8 сек	259 км/ч
Ио	0,182	1,789		10,6 сек	68 км/ч
Европа	0,134	1,314		12,3 сек	58 км/ч
Ганимед	0,145	1.426		11,8 сек	61 км/ч
Каллисто	0,126	1,24		12,7 сек	57 км/ч
Сатурн	1,139	11,19		4,2 сек	170 км/ч
Титан	0,138	1,352		12,2 сек	59 км/ч
Уран	0,917	9,01		4,7 сек	153 км/ч
Титания	0,039	0,379		23,0 сек	31 км/ч
Оберон	0,035	0,347		24,0 сек	30 км/ч
Нептун	1,148	11,28		4,2 сек	171 км/ч
Тритон	0,079	0,779		16,0 сек	45 км/ч
Плутон	0,063	0,62		18,1 сек	40 км/ч
Эрида	0,0814	0,8	(приблизит.)	15,8 сек	46 км/ч

См. также

Примечания

Ссылки

Литература

• Миронов В.С. Курс гравиразведки. — Л. : Недра, 1980. — 543 с.