Точки Лагра́нжа , точки либра́ции ( лат. librātiō — раскачивание) или L-точки — точки в системе из двух массивных тел, в которых третье тело с пренебрежимо малой массой, не испытывающее воздействия никаких других сил , кроме гравитационных со стороны двух первых тел, может оставаться неподвижным относительно этих тел.

Более точно точки Лагранжа представляют собой частный случай при решении так называемой ограниченной задачи трёх тел — когда орбиты всех тел являются круговыми и масса одного из них намного меньше массы любого из двух других. В этом случае можно считать, что два массивных тела обращаются вокруг их общего центра масс с постоянной угловой скоростью . В пространстве вокруг них существуют пять точек, в которых третье тело с пренебрежимо малой массой может оставаться неподвижным во вращающейся системе отсчёта, связанной с массивными телами. В этих точках гравитационные силы, действующие на малое тело, уравновешиваются центробежной силой .

Точки Лагранжа получили своё название в честь математика Жозефа Луи Лагранжа , который первым в 1772 году привёл решение математической задачи, из которого следовало существование этих особых точек.

Расположение точек Лагранжа

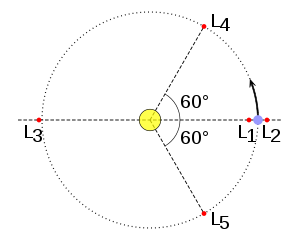
Все точки Лагранжа лежат в плоскости орбит массивных тел и обозначаются заглавной латинской буквой L с числовым индексом от 1 до 5. Первые три точки расположены на линии, проходящей через оба массивных тела. Эти точки Лагранжа называются коллинеарными и обозначаются L ₁ , L ₂ и L ₃ . Точки L ₄ и L ₅ называются треугольными или троянскими. Точки L ₁ , L ₂ , L ₃ являются точками неустойчивого равновесия, в точках L ₄ и L ₅ равновесие устойчивое.

L ₁ находится между двумя телами системы, ближе к менее массивному телу; L ₂ — снаружи, за менее массивным телом; и L ₃ — за более массивным. В системе координат с началом отсчёта в центре масс системы и с осью, направленной от центра масс к менее массивному телу, координаты этих точек в первом приближении по α рассчитываются с помощью следующих формул :

${\displaystyle r_{1}=\left(R\left[1-\left({\frac {\alpha }{3}}\right)^{1/3}\right],0\right)}$

${\displaystyle r_{2}=\left(R\left[1+\left({\frac {\alpha }{3}}\right)^{1/3}\right],0\right)}$

${\displaystyle r_{3}=\left(-R\left[1+{\frac {5}{12}}\alpha \right],0\right)}$

где ${\displaystyle \alpha ={\frac {M_{2}}{M_{1}+M_{2}}}}$ ,

R — расстояние между телами,

M ₁ — масса более массивного тела,

M ₂ — масса второго тела.

L ₁

Точка L ₁ лежит на прямой, соединяющей два тела с массами M ₁ и M ₂ (M ₁ > M ₂ ), и находится между ними, вблизи второго тела. Её наличие обусловлено тем, что гравитация тела M ₂ частично компенсирует гравитацию тела M ₁ . При этом чем больше M ₂ , тем дальше от него будет располагаться эта точка.

Пример: Объекты, которые движутся вокруг Солнца ближе, чем Земля, как правило, имеют меньшие орбитальные периоды, чем у Земли, если они не входят в зону влияния земного притяжения. Если объект находится непосредственно между Землёй и Солнцем, то действие земной силы тяжести отчасти компенсирует влияние гравитации Солнца, за счёт этого происходит увеличение орбитального периода объекта. Причём чем ближе к Земле находится объект, тем сильнее этот эффект. И наконец, на определённом приближении к планете — в точке L ₁ — действие земной силы тяжести уравновешивает влияние солнечной гравитации настолько, что период обращения объекта вокруг Солнца становится равным периоду обращения Земли. Для нашей планеты расстояние до точки L ₁ составляет около 1,5 млн км. Притяжение Солнца здесь (118 мкм/с² ) на 2 % сильнее, чем на орбите Земли (116 мкм/с² ), тогда как снижение требуемой центростремительной силы вдвое меньше (59 мкм/с² ). Сумма этих двух эффектов уравновешивается притяжением Земли, которое составляет здесь также 177 мкм/с² .

Использование

В системе Солнце— Земля точка L ₁ может быть идеальным местом для размещения космической обсерватории для наблюдения Солнца, которое в этом месте никогда не перекрывается ни Землёй, ни Луной. Первым аппаратом, работавшим вблизи этой точки, был запущенный в августе 1978 года аппарат ISEE-3 . Аппарат вышел на периодическую гало-орбиту вокруг этой точки 20 ноября 1978 года и был сведён с этой орбиты 10 июня 1982 года (для исполнения новых задач) . На такой же орбите с мая 1996 года работает аппарат SOHO . Аппараты ACE , WIND и DSCOVR находятся на квази-периодических орбитах Лиссажу́ близ этой же точки, соответственно, с 12 декабря 1997 , 16 ноября 2001 и 8 июня 2015 года . В 2016—2017 годах также в окрестностях этой точки проводил эксперименты аппарат LISA Pathfinder .

Лунная точка L ₁ (в системе Земля — Луна ; удалена от центра Земли примерно на 315 тыс.км ) может стать идеальным местом для строительства космической пилотируемой орбитальной станции , которая, располагаясь на пути между Землёй и Луной, позволила бы легко добраться до Луны с минимальными затратами топлива и стать ключевым узлом грузового потока между Землёй и её спутником .

L ₂

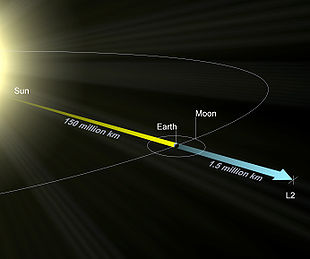
Точка L ₂ лежит на прямой, соединяющей два тела с массами M ₁ и M ₂ (M ₁ > M ₂ ), и находится за телом с меньшей массой. Точки L ₁ и L ₂ располагаются на одной линии и в пределе M ₁ ≫ M ₂ симметричны относительно M ₂ . В точке L ₂ гравитационные силы, действующие на тело, компенсируют действие центробежных сил во вращающейся системе отсчёта.

Пример: у объектов, расположенных за орбитой Земли (от Солнца), орбитальный период почти всегда больше, чем у Земли. Но дополнительное влияние на объект силы тяжести Земли, помимо действия солнечной гравитации, приводит к увеличению скорости вращения и уменьшению времени оборота вокруг Солнца, в результате в точке L ₂ орбитальный период объекта становится равным орбитальному периоду Земли.

Если M ₂ много меньше по массе, чем M ₁ , то точки L ₁ и L ₂ находятся на примерно одинаковом расстоянии r от тела M ₂ , равном радиусу сферы Хилла :

${\displaystyle r\approx R{\sqrt[{3}]{\frac {M_{2}}{3M_{1}}}}}$

где R — расстояние между компонентами системы.

Это расстояние можно описать как радиус круговой орбиты вокруг M ₂ , для которой период обращения в отсутствие M ₁ в ${\displaystyle {\sqrt {3}}\approx 1{,}73}$ раз меньше, чем период обращения M ₂ вокруг M ₁ .

Использование

Точка L ₂ системы Солнце—Земля (1 500 000 км от Земли) является идеальным местом для расположения орбитальных космических обсерваторий и телескопов. Поскольку объект в точке L ₂ способен длительное время сохранять свою ориентацию относительно Солнца и Земли, производить его экранирование и калибровку становится гораздо проще. Однако эта точка расположена немного дальше земной тени (в области полутени ) , так что солнечная радиация блокируется не полностью. На гало-орбитах вокруг этой точки на 2021 год располагались аппараты Gaia и Спектр-РГ . Ранее там действовали такие телескопы как « Планк » и « Гершель ». С 2022 года это место расположения крупнейшего космического телескопа в истории имени Джеймса Уэбба .

Точка L ₂ системы Земля—Луна (61 500 км от Луны) может использоваться для обеспечения спутниковой связи с объектами на обратной стороне Луны ; впервые эту возможность реализовал в 2018 году китайский спутник Цюэцяо , ретранслятор первой в истории миссии на обратной стороне Луны Чанъэ-4 .

L ₃

Точка L ₃ лежит на прямой, соединяющей два тела с массами M ₁ и M ₂ ( M ₁ > M ₂ ), и находится за телом с бо́льшей массой. Так же, как для точки L ₂ , в этой точке гравитационные силы компенсируют действие центробежных сил.

Пример: точка L ₃ в системе Солнце — Земля находится за Солнцем, на противоположной стороне земной орбиты. Однако, несмотря на свою малую (по сравнению с солнечной) гравитацию, Земля всё же оказывает там небольшое влияние, поэтому точка L ₃ находится не на самой орбите Земли, а чуть ближе к Солнцу (на 263 км , или около 0,0002 %) , так как вращение происходит не вокруг Солнца, а вокруг барицентра . В результате в точке L ₃ достигается такое сочетание гравитации Солнца и Земли, что объекты, находящиеся в этой точке, движутся с таким же орбитальным периодом, как и наша планета.

До начала космической эры среди писателей-фантастов была очень популярна идея о существовании на противоположной стороне земной орбиты в точке L ₃ другой аналогичной ей планеты, называемой « Противоземлёй », которая из-за своего расположения была недоступна для прямых наблюдений. Однако на самом деле из-за гравитационного влияния других планет точка L ₃ в системе Солнце — Земля является крайне неустойчивой. Так, во время гелиоцентрических соединений Земли и Венеры по разные стороны Солнца, которые случаются каждые 20 месяцев , Венера находится всего в 0,3 а. е. от точки L ₃ и таким образом оказывает очень серьёзное влияние на её расположение относительно земной орбиты. Кроме того, из-за движения Солнца вокруг центра масс системы Солнце — Юпитер, при котором оно последовательно занимает положение по разные стороны от этой точки, и эллиптичности земной орбиты, так называемая «Противоземля» всё равно время от времени была бы доступна для наблюдений и обязательно была бы замечена. Ещё одним эффектом, выдающим её существование, была бы её собственная гравитация: влияние тела размером уже порядка 150 км и более на орбиты других планет было бы заметно . С появлением возможности производить наблюдения с помощью космических аппаратов и зондов было достоверно показано, что в этой точке нет объектов размером более 100 м ^{[ нет в источнике ]} .

Орбитальные космические аппараты и спутники, расположенные вблизи точки L ₃ , могут постоянно следить за различными формами активности на поверхности Солнца — в частности, за появлением новых пятен или вспышек, — и оперативно передавать информацию на Землю (например, в рамках системы раннего предупреждения о космической погоде NOAA ). Кроме того, информация с таких спутников может быть использована для обеспечения безопасности дальних пилотируемых полётов, например к Марсу или астероидам. В 2010 году были изучены несколько вариантов запуска подобного спутника

L ₄ и L ₅

Если на основе линии, соединяющей оба тела системы, построить два равносторонних треугольника, две вершины которых соответствуют центрам тел M ₁ и M ₂ , то точки L ₄ и L ₅ будут соответствовать положению третьих вершин этих треугольников, расположенных в плоскости орбиты второго тела в 60 градусах впереди и позади него.

Наличие этих точек и их высокая стабильность обусловливается тем, что, поскольку расстояния до двух тел в этих точках одинаковы, то силы притяжения со стороны двух массивных тел соотносятся в той же пропорции, что их массы, и таким образом результирующая сила направлена на центр масс системы; кроме того, геометрия треугольника сил подтверждает, что результирующее ускорение связано с расстоянием до центра масс той же пропорцией, что и для двух массивных тел. Так как центр масс является одновременно и центром вращения системы, результирующая сила точно соответствует той, которая нужна для удержания тела в точке Лагранжа в орбитальном равновесии с остальной системой. (На самом деле, масса третьего тела и не должна быть пренебрежимо малой). Данная треугольная конфигурация была обнаружена Лагранжем во время работы над задачей трёх тел . Точки L ₄ и L ₅ называют треугольными (в отличие от коллинеарных).

Также точки называют троянскими : это название происходит от троянских астероидов Юпитера , которые являются самым ярким примером проявления этих точек. Они были названы в честь героев Троянской войны из « Илиады » Гомера , причём астероиды в точке L ₄ получают имена греков, а в точке L ₅ — защитников Трои ; поэтому их теперь так и называют «греками» (или « ахейцами ») и «троянцами».

Расстояния от центра масс системы до этих точек в координатной системе с центром координат в центре масс системы рассчитываются по следующим формулам:

${\displaystyle r_{4}=\left({\frac {R}{2}}\beta ,{\frac {{\sqrt {3}}R}{2}}\right)}$

${\displaystyle r_{5}=\left({\frac {R}{2}}\beta ,-{\frac {{\sqrt {3}}R}{2}}\right)}$

где

${\displaystyle \beta ={\frac {M_{1}-M_{2}}{M_{1}+M_{2}}}}$ ,

R — расстояние между телами,

M ₁ — масса более массивного тела,

M ₂ — масса второго тела.

Расположение точек Лагранжа в системе Солнце — Земля

L ₁ =(1,48104 ⋅ 10 ¹¹ , 0)

L ₂ =(1,51092 ⋅ 10 ¹¹ , 0)

L ₃ =(-1,49598 ⋅ 10 ¹¹ , 0)

L ₄ =(7,47985 ⋅ 10 ¹⁰ , 1,29556 ⋅ 10 ¹¹ )

L ₅ =(7,47985 ⋅ 10 ¹⁰ , −1,29556 ⋅ 10 ¹¹ )

Примеры:

• В 2010 году в системе Солнце — Земля в троянской точке L ₄ обнаружен астероид 2010 TK ₇ , а в 2020 году — 2020 XL ₅ . В L ₅ пока не обнаружено троянских астероидов, но там наблюдается довольно большое скопление межпланетной пыли.
• По некоторым наблюдениям, в точках L ₄ и L ₅ системы Земля — Луна находятся очень разрежённые скопления межпланетной пыли — облака Кордылевского .
• В системе Солнце — Юпитер в окрестностях точек L ₄ и L ₅ находятся так называемые троянские астероиды . По состоянию на 21 октября 2010 известно около четырёх с половиной тысяч астероидов в точках L ₄ и L ₅ .
• Троянские астероиды в точках L ₄ и L ₅ есть не только у Юпитера, но и у других планет-гигантов .
• Другим интересным примером является спутник Сатурна Тефия , в точках L ₄ и L ₅ которой находятся два небольших спутника — Телесто и Калипсо . Ещё одна пара спутников известна в системе Сатурн — Диона : Елена в точке L ₄ и Полидевк в точке L ₅ . Тефия и Диона в сотни раз массивнее своих «подопечных», и гораздо легче Сатурна, что делает систему стабильной.
• Один из сценариев модели ударного формирования Луны предполагает, что гипотетическая протопланета ( планетезималь ) Тейя , в результате столкновения которой с Землёй образовалась Луна , сформировалась в точке Лагранжа L ₄ или L ₅ системы Солнце — Земля .
• Первоначально считалось, что в системе Kepler-223 две из четырёх планет обращаются вокруг своего солнца по одной орбите на расстоянии 60 градусов . Однако дальнейшие исследования показали, что данная система не содержит коорбитальных планет .

Равновесие в точках Лагранжа

Тела, помещённые в коллинеарных точках Лагранжа, находятся в неустойчивом равновесии. Например, если объект в точке L ₁ слегка смещается вдоль прямой, соединяющей два массивных тела, сила, притягивающая его к тому телу, к которому оно приближается, увеличивается, а сила притяжения со стороны другого тела, наоборот, уменьшается. В результате объект будет всё больше удаляться от положения равновесия.

Такая особенность поведения тел в окрестностях точки L ₁ играет важную роль в тесных двойных звёздных системах . Полости Роша компонент таких систем соприкасаются в точке L ₁ , поэтому, когда одна из звёзд-компаньонов в процессе эволюции заполняет свою полость Роша, вещество перетекает с одной звезды на другую именно через окрестности точки Лагранжа L ₁ .

Несмотря на это, существуют стабильные замкнутые орбиты (во вращающейся системе координат) вокруг коллинеарных точек либрации, по крайней мере, в случае задачи трёх тел. Если на движение влияют и другие тела (как это происходит в Солнечной системе ), вместо замкнутых орбит объект будет двигаться по квазипериодическим орбитам, имеющим форму фигур Лиссажу . Несмотря на неустойчивость такой орбиты, космический аппарат может оставаться на ней в течение длительного времени, затрачивая относительно небольшое количество топлива .

В отличие от коллинеарных точек либрации, в троянских точках обеспечивается устойчивое равновесие, если M ₁ / M ₂ > 24,96 . При смещении объекта возникают силы Кориолиса , которые искривляют траекторию, и объект движется по устойчивой орбите вокруг точки либрации.

Практическое применение

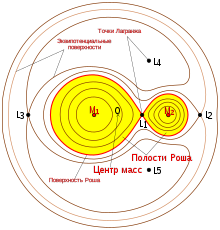
Исследователи в области космонавтики давно уже обратили внимание на точки Лагранжа. Например, в точке L ₁ системы Земля — Солнце удобно разместить космическую солнечную обсерваторию — она никогда не будет попадать в тень Земли, а значит, наблюдения могут вестись непрерывно. Точка L ₂ подходит для космического телескопа — здесь Земля почти полностью заслоняет солнечный свет, да и сама не мешает наблюдениям, поскольку обращена к L ₂ неосвещённой стороной. Точка L ₁ системы Земля — Луна удобна для размещения ретрансляционной станции в период освоения Луны. Она будет находиться в зоне прямой видимости для большей части обращённого к Земле полушария Луны, а для связи с ней понадобятся передатчики в десятки раз менее мощные, чем для связи с Землёй.

В настоящее время несколько космических аппаратов , в первую очередь, астрофизических обсерваторий, размещены или планируются к размещению в различных точках Лагранжа Солнечной системы :

Точка L ₁ системы Земля—Солнце :

• ISEE-3 International Cometary Explorer (запущен в 1978 году)
• Космический аппарат WIND , предназначенный для исследования солнечного ветра (запущен в 1994 году).
• SOHO ( англ. Solar and Heliospheric Observatory , «Солнечная и гелиосферная обсерватория») (запущен в 1995 году).
• Advanced Composition Explorer (запущен в 1997 году).
• Genesis — космический аппарат НАСА , предназначенный для сбора и доставки на Землю образцов солнечного ветра . В в 2001 году запущен на орбиту вокруг точки Лагранжа L1 с последующим облётом точки L2 (вернулся на землю в 2004 году).
• Космическая обсерватория DSCOVR (запущена в 2015 году).
• LISA Pathfinder , запущенная в 2015 году, осуществляла проверку технологий, необходимых для планируемой постройки будущей гравитационной обсерватории eLISA .
• ^* , индийская солнечная обсерватория (запущена в 2023 году).
• Лазерная интерферометрическая космическая антенна eLISA предназначена для регистрации гравитационных волн и проверки общей теории относительности (запуск запланирован на 2034 год).

Точка L ₂ системы Земля—Солнце :

• Космический аппарат WMAP , изучающий реликтовое излучение (запущен в 2001 году).
• Космические телескопы « Гершель » и « Планк », (запущены в 2009 году) .
• Европейский телескоп « Gaia » (запущен в 2013 году).
• Космическая обсерватория Спектр-РГ (запущена в 2019 году) .
• Орбитальная инфракрасная обсерватория « Джеймс Уэбб » (запущена в 2021 году) .
• Космический телескоп PLATO также планируется разместить в точке L ₂ (запуск запланирован на 2026 год).

Другие точки Лагранжа :

• в сентябре-октябре 2009 года два аппарата STEREO совершили транзит через точки L ₄ и L ₅ .
• JIMO ( Jupiter Icy Moons Orbiter ) — отменённый проект NASA по исследованию спутников Юпитера, который должен был активно использовать систему точек Лагранжа для перехода от одного спутника к другому с минимальными затратами топлива. Этот манёвр получил название «лестница Лагранжа» .
• THEMIS несколько аппаратов вокруг точек L1 и L2 системы Земля-Луна
• ретрансляционный спутник Цюэцяо , выведенный на орбиту 20 мая 2018 года с помощью ракеты Чанчжэн-4C , циркулирует по гало-орбите вокруг точки Лагранжа L2 системы Земля-Луна .

Упоминание в культуре

Точки Лагранжа довольно популярны в научно-фантастических произведениях, посвящённых освоению космоса. Авторы часто помещают в них обитаемые или автоматические станции — см., например, «Возвращение к звёздам» Гарри Гаррисона , « Глубина в небе » Вернора Винджа , « Нейромант » Уильяма Гибсона , « Семиевие » Нила Стивенсона , телесериал « Вавилон-5 », аниме « Mobile Suit Gundam », компьютерные игры Prey , Borderlands 2 , (место расположения казино «Хрустальный дворец») .

Иногда в точки Лагранжа помещают и более интересные объекты — мусорные свалки («Единение разумов» Чарльза Шеффилда , «Нептунова арфа» Андрея Балабухи ), инопланетные артефакты («Защитник» Ларри Нивена ) и даже целые планеты («Планета, с которой не возвращаются» Пола Андерсона ). Айзек Азимов предлагал отправлять в точки Лагранжа радиоактивные отходы («Вид с высоты»).

Московская пост-роковая группа Mooncake в 2008 году выпустила альбом Lagrange Points , на обложке которого схематически изображены все точки Лагранжа.

См. также

• Колонизация точек Лагранжа

Примечания

Комментарии

Источники

Ссылки

• (англ.)
• David Peter Stern . (англ.)