Interested Article - Траектория

- 2020-06-10
- 1

Траекто́рия материа́льной то́чки — линия в пространстве , являющаяся множеством геометрических точек, где можно найти материальную точку , в физической задаче . Вид траектории свободной материальной точки зависит от действующих на точку сил , начальных условий движения и от выбора системы отсчёта , а несвободной — также от наложенных связей .
Понятие о траектории имеет смысл и в отрыве от какого-либо реального движения. Но траектория, изображаемая в некоторой системе координат, сама по себе не даёт информации о причинах движения тела по ней, пока не выполнен анализ конфигурации поля действующих на тело сил в той же координатной системе .
Способы задания траектории
Вид траектории не зависит от особенностей её прохождения материальной точкой, поэтому для задания траектории могут применяться не физические законы или модели, а средства дифференциальной геометрии .
Так, траектория иногда задаётся функцией/функциями, связывающ-ей/-ими координаты на линии движения точки:
- в случае движения по прямой,
- для плоского случая,
- и в объёмном случае.
Но здесь необходимы взаимная однозначность связи координат и отсутствие повторного прохождения материальной точкой каких-либо участков. Например, если тело двигалось по отрезку от до и назад, то траектория является «двойной» (туда-обратно) линией, что будет упущено при вышеуказанном подходе. Тем не менее, такое координатное задание траектории во многих простых ситуациях удобно.
В общем случае движение материальной точки в кинематике описывается зависимостью радиус-вектора от времени:
- .
Такая зависимость представляет траекторию, давая избыток информации — кроме формы прочерчиваемой точкой геометрической линии, имея , можно получить скорость и другие параметры движения. Задание подразумевает задание изменений трёх декартовых координат во времени:
- ,
где , , — орты . Присутствие здесь времени , казалось бы, противоречит независимости траектории от деталей движения по ней, но на самом деле для задания именно траектории на место в выражениях , , можно подставлять любую взаимно однозначную функцию . Произвол не скажется на форме траектории, а будет «менять» скорость прохождения: скажем, при замене на скорость во всех точках траектории удвоится.
В выбранной системе отсчета, кривая, описываемая концом радиус-вектора в пространстве, может быть представлена в виде сопряжённых дуг различной кривизны , находящихся в общем случае в пересекающихся плоскостях . При этом кривизна каждой дуги определяется её радиусом кривизны (не путать с радиус-вектором ), направленным к дуге из мгновенного (не путать с началом отсчета радиус-векторов), находящегося в той же плоскости, что и сама дуга. Прямая линия рассматривается как предельный случай кривой , радиус кривизны которой может считаться равным бесконечности .
Траектория и смежные понятия
- Закон движения — зависимость радиус-вектора точки от времени ;
- Путь — криволинейная координата вдоль траектории материальной точки (обычно обозначается символом );
- Длина пути — длина траектории , вычисляемая как
- ,
- где цифры 1 и 2 маркируют начальное и конечное положения точки, соответственно;
- Перемещение — вектор из начального положения точки в конечное
- ,
- при этом всегда ;
- Радиус кривизны — радиус дуги окружности, наилучшим образом аппроксимирующей траекторию в заданной точке.
Скорость материальной точки всегда направлена по касательной к дуге, используемой для описания траектории. При этом существует связь между величиной скорости , нормальным ускорением и радиусом кривизны траектории в конкретной геометрической точке:
- .
Не всякое движение с известной скоростью по кривой известного радиуса и найденное по приведённой выше формуле нормальное (центростремительное) ускорение связано с проявлением силы, направленной по нормали к траектории ( центростремительной силы ). Так, найденное по данным фотографии суточного движения светил ускорение любой из звёзд отнюдь не говорит о существовании вызывающей это ускорение силы, притягивающей её к Полярной звезде как центру вращения.
Траектория и уравнения динамики
Представление траектории как следа, оставляемого движением материальной точки, связывает чисто кинематическое понятие о траектории, как геометрической проблеме, с динамикой движения материальной точки, то есть проблемой определения причин её движения. Фактически, решение уравнений Ньютона (при наличии полного набора исходных данных) даёт траекторию материальной точки.
Движение свободной материальной точки
В соответствии с первым законом Ньютона , иногда называемым законом инерции , должна существовать такая система, в которой свободное тело сохраняет (как вектор) свою скорость. Такая система отсчёта называется инерциальной . Траекторией такого движения является прямая линия , а само движение называется равномерным и прямолинейным.
Движение под действием внешних сил
- в инерциальной системе отсчёта
Если в инерциальной системе скорость движения объекта ( для неподвижного в данной системе наблюдателя ) с массой меняется по направлению, даже оставаясь прежней по величине, то есть тело производит поворот и движется по дуге с радиусом кривизны , то значит, это тело испытывает нормальное ускорение . Причиной, вызывающей это ускорение, является центростремительная сила, прямо пропорциональная этому ускорению. В этом состоит суть второго закона Ньютона :
- ,
где есть векторная сумма сил, действующих на тело, — его ускорение, а — инертная масса .
В общем случае тело не бывает свободно в своём движении, и на его положение, а в некоторых случаях и на скорость , налагаются ограничения — связи . Если связи накладывают ограничения только на координаты тела, то такие связи называются геометрическими. Если же они распространяются и на скорости, то они называются кинематическими. Если уравнение связи может быть проинтегрировано во времени, то такая связь называется голономной .
Действие связей на систему движущихся тел описывается силами, называемыми реакциями связей. В таком случае сила, входящая в левую часть выражения закона Ньютона, есть векторная сумма активных (внешних) сил и реакции связей.
Существенно, что в случае голономных связей становится возможным описать движение механических систем в обобщённых координатах , входящих в уравнения Лагранжа . Число этих уравнений зависит лишь от числа степеней свободы системы и не зависит от количества входящих в систему тел, положение которых необходимо определять для полного описания движения.
Если же связи, действующие в системе , то есть в них не происходит переход энергии движения в другие виды энергии, то при решении уравнений Лагранжа автоматически исключаются все неизвестные реакции связей.
Наконец, если действующие силы принадлежат к классу потенциальных , то при соответствующем обобщении понятий становится возможным использования уравнений Лагранжа не только в механике, но и других областях физики.
Действующие на материальную точку силы в этом понимании однозначно определяют форму траектории её движения (при известных начальных условиях). Обратное утверждение в общем случае несправедливо, поскольку одна и та же траектория может иметь место при различных комбинациях активных сил и реакций связи.
- в неинерциальной системе отсчёта
Если система отсчёта неинерциальна (то есть движется с неким ускорением относительно инерциальной системы отсчёта), то в ней также возможно использование закона Ньютона, однако в левой части необходимо учесть так называемые силы инерции (в том числе, центробежную силу и силу Кориолиса , связанные с вращением неинерциальной системы отсчёта) .
Значимость выбора системы отсчёта

Уточнение о «привязке» траектории к выбору координатной системы принципиально, так как форма траектории зависит от этого выбора . Качественные и количественные различия траекторий возникают и между инерциальными системами, и если одна или обе системы неинерциальны.
Наблюдаемость траектории
Возможно наблюдение траектории при неподвижности объекта, но при движении системы отсчёта. Так, звёздное небо может послужить хорошей моделью инерциальной и неподвижной системы отсчёта. Однако при длительной экспозиции эти звёзды представляются движущимися по круговым траекториям.
Возможен и противоположный случай, когда тело явно движется, но траектория в проекции на плоскость наблюдения является одной неподвижной точкой. Это, например, случай летящей прямо в глаз наблюдателя пули или уходящего от него поезда.
Модификация формы траектории
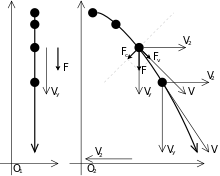
Нередко оказывается, что форма траектории зависит от системы отсчёта , избранной для описания движения материальной точки радикальным образом. Так, прямолинейное равноускоренное движение (скажем, свободое падение) в одной инерциальной системе в общем случае будет параболическим в другой равномерно двигающейся инерциальной системе отсчёта (см. рис.).
В соответствии с принципом относительности Галилея , существует бесконечное множество равноправных инерциальных систем (ИСО), движение которых одна относительно другой не может быть установлено никаким образом путём наблюдения любых процессов и явлений, происходящих только в этих системах. Прямая траектория равномерного движения объекта в одной системе будет выглядеть также прямой в любой другой инерциальной системе, хотя величина и направление скорости будут зависеть от выбора системы, то есть от величины и направления их относительной скорости.
Вместе с тем Принцип Галилея не утверждает , что одно и то же явление, наблюдаемое из двух разных ИСО, будут выглядеть одинаково. Поэтому рисунок предупреждает о двух типичных ошибках, связанных с забвением того, что:
1. Истинно, что любой вектор (в том числе вектор силы) может быть разложен по крайней мере на две составляющие. Но это разложение совершенно произвольно и не значит, что такие компоненты существуют в действительности. Для подтверждения их реальности должна привлекаться дополнительная информация , в любом случае не взятая из анализа формы траектории. Например, по рисунку 2 невозможно определить природу силы F, так же как невозможно утверждать, что она сама является или не является суммой сил разной природы. Можно лишь утверждать, что на изображённом участке она постоянна, и что для формирования наблюдаемой в данной СО криволинейности траектории служит вполне определённая в данной СО центростремительная часть этой силы. Зная лишь траекторию материальной точки в какой-либо инерциальной системе отсчёта и её скорость в каждый момент времени, нельзя определить природу сил, действовавших на неё.
2. Даже в случае наблюдения из ИСО, форма траектории ускоренно движущегося тела будет определяться не только действующими на него силами, но и выбором этой ИСО, никак на эти силы не влияющим. Центростремительная сила , показанная на рисунке 2, получена формально, и её величина непосредственно зависит от выбора ИСО.
Пример для вращающейся системы

Представим себе работника театра, передвигающегося в над сценой по отношению к зданию театра равномерно и прямолинейно и несущего над вращающейся сценой дырявое ведро с краской. Он будет оставлять на ней след от падающей краски в форме раскручивающейся спирали (если движется от центра вращения сцены) и закручивающейся — в противоположном случае. В это время его коллега, отвечающий за чистоту вращающейся сцены и на ней находящийся, будет поэтому вынужден нести под первым недырявое ведро, постоянно находясь под первым. И его движение по отношению к зданию также будет равномерным и прямолинейным , хотя по отношению к сцене, которая является неинерциальной системой , его движение будет искривлённым и неравномерным . Более того, для того, чтобы противодействовать сносу в направлении вращения, он должен мышечным усилием преодолевать действие силы Кориолиса , которое не испытывает его верхний коллега над сценой, хотя траектории обоих в инерциальной системе здания театра будут представлять прямые линии .
Но можно себе представить, что задачей рассматривающихся здесь коллег является именно нанесение прямой линии на вращающейся сцене . В этом случае нижний должен потребовать от верхнего движения по кривой, являющейся зеркальным отражением следа от ранее пролитой краски,оставаясь при этом над любой точкой прямой, проходящей в избранном радиальном направлении. Следовательно, прямолинейное движение в неинерциальной системе отсчёта не будет являться таковым для наблюдателя в инерциальной системе .
Более того, равномерное движение тела в одной системе, может быть неравномерным в другой. Так, две капли краски, упавшие в разные моменты времени из дырявого ведра, как в собственной системе отсчёта, так и в системе неподвижного по отношению к зданию нижнего коллеги (на уже прекратившей вращение сцене), будут двигаться по прямой (к центру Земли). Различие будет заключаться в том, что для нижнего наблюдателя это движение будет ускоренным , а для верхнего его коллеги, если он, оступившись, будет падать , двигаясь вместе с любой из капель, расстояние между каплями будет увеличиваться пропорционально первой степени времени, то есть взаимное движение капель и их наблюдателя в его ускоренной системе координат будет равномерным со скоростью , определяемой задержкой между моментами падения капель; здесь — ускорение свободного падения .
Поэтому форма траектории и скорость движения по ней тела, рассматриваемая в некоторой системе отсчёта, о которой заранее ничего не известно , не даёт однозначного представления о силах, действующих на тело. Решить вопрос о том, является ли эта система в достаточной степени инерциальной, можно лишь на основе анализа причин возникновения действующих сил.
Таким образом, в неинерциальной системе, во-первых, кривизна траектории и/или непостоянство скорости являются недостаточным аргументом в пользу утверждения о том, что на движущееся по ней тело действуют внешние силы, которые в конечном случае могут быть объяснены гравитационными или электромагнитными полями, а во-вторых, прямолинейность траектории является недостаточным аргументом в пользу утверждения о том, что на движущееся по ней тело не действуют никакие силы.
Бестраекторное движение
Согласно квантовомеханическим представлениям, в отношении движения микрочастицы (электрона или другой) в ограниченном пространстве следует говорить не о траектории , а об эволюции плотности вероятности обнаружить частицу в заданной точке . Эта плотность вероятности характеризуется квадратом модуля волновой функции . Зависимость от её аргументов определяется с помощью уравнения Шрёдингера . Располагая волновой функцией, можно найти меняющееся со временем положение «центроида» (интегрирование – по всему доступному частице объёму). В пределе, когда длина волны де Бройля частицы несопоставимо меньше размера пространственной области движения, такой подход становится эквивалентным привычному расчёту траектории.
См. также
Примечания
- Понятие траектории достаточно наглядно может быть проиллюстрировано трассой бобслея (если по условиям задачи можно пренебречь её шириной). И именно трассой, а не самим бобом .
- Физический энциклопедический словарь, статья Траектория , стр. 764 / гл. ред. А. М. Прохоров — М.: Советская энциклопедия (1984).
- Так улица, в начале которой висит знак «кирпич» останется в принципе траекторией движения по ней. А поезда разной массы, движущиеся под различными тяговыми усилиями на сцепных крюках локомотивов и потому с разной скоростью, будут двигаться по одной и той же траектории, определяемой формой рельсового пути, налагающего на движение несвободного тела (поезда) конкретные , интенсивность которых будет в каждом случае различной
- ↑ С. Э. Хайкин . Силы инерции и невесомость. М., 1967 г. Изд-во «Наука». Главная редакция физико-математической литературы.
- Физический энциклопедический словарь/ Гл. ред. А. М. Прохоров. Ред.кол. Д. М. Алексеев, А. М. Бонч-Бруевич, А. С. Боровик-Романов и др. М. : Сов.энциклопедия, 1983. — 323 с.,ил, 2 л.цв.ил. страница 282.
- Так, Луна обращается вокруг Земли только в системе отсчёта, связанной с их общим центром гравитации (находится внутри Земного шар). В системе же отсчёта, началом которой является Солнце, Луна обращается вокруг него по той же эллиптической орбите, что и Земля, но с периодическими отклонениями от неё на величину расстояния от Луны до Земли. Никакого взаимного обращения этих небесных тел в этом случае просто нет. Наличие земного притяжения для объяснения формы траектории Луны в системе координат, связанной с Солнцем, вообще не обязательно. Так, исчезни Земля, Луна могла бы продолжать двигаться, как самостоятельное небесное тело, по той же самой старой траектории, а её периодические возмущения можно было бы тогда в качестве гипотезы объяснить изменением силы тяготения, скажем, за счёт вариации массы Солнца по причине пульсации его светимости (что, кстати, и наблюдается в определённых пределах в действительности). И обе упомянутые формы траектории истинны и оба объяснения их формы на основании правильно проведённого анализа действующих сил справедливы. Но они исключают друг друга, как исключается возможность одновременного рассмотрения при выборе той или иной системы координат.
- : [ 10 августа 2022 ] / Д. В. Гальцов // Великий князь — Восходящий узел орбиты. — М. : Большая российская энциклопедия, 2006. — С. 641-642. — ( Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 5). — ISBN 5-85270-334-6 .
В физике есть ещё одна формула измерения траектории (пути): s=4Atv, где A - амплитуда, t - время, v - частота колебаний
Литература
- Ньютон И. Математические начала натуральной философии. Пер. и прим. А. Н. Крылова. М.: Наука, 1989
- Фриш С. А. и Тиморева А. В. Курс общей физики, Учебник для физико-математических и физико-технических факультетов государственных университетов, Том I. М.: ГИТТЛ, 1957
Ссылки
- 2020-06-10
- 1






















































