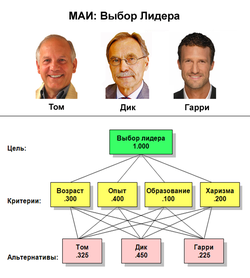
Метод анализа иерархий (МАИ) — математический инструмент системного подхода к сложным проблемам принятия решений.

МАИ не предписывает лицу, принимающему решение ( ЛПР ), какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант (альтернативу), который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к её решению.

Этот метод разработан американским математиком Томасом Л. Саати , который написал о нём книги, разработал программные продукты и в течение 20 лет проводил симпозиумы ISAHP ( англ. International Symposium on Analytic Hierarchy Process ). МАИ широко используется на практике и активно развивается учёными всего мира. В его основе наряду с математикой заложены и психологические аспекты. МАИ позволяет понятным и рациональным образом структурировать сложную проблему принятия решений в виде иерархии, сравнить и выполнить количественную оценку альтернативных вариантов решения. Метод анализа иерархий используется во всем мире для принятия решений в разнообразных ситуациях: от управления на межгосударственном уровне до решения отраслевых и частных проблем в бизнесе , промышленности , здравоохранении и образовании .

Для компьютерной поддержки МАИ существуют программные продукты, разработанные различными компаниями.

Анализ проблемы принятия решений в МАИ начинается с построения иерархической структуры, которая включает цель, критерии, альтернативы и другие рассматриваемые факторы, влияющие на выбор. Эта структура отражает понимание проблемы лицом, принимающим решение.

Каждый элемент иерархии может представлять различные аспекты решаемой задачи, причем во внимание могут быть приняты как материальные, так и нематериальные факторы, измеряемые количественные параметры и качественные характеристики, объективные данные и субъективные экспертные оценки . Иными словами, анализ ситуации выбора решения в МАИ напоминает процедуры и методы аргументации, которые используются на интуитивном уровне.

Следующим этапом анализа является определение приоритетов, представляющих относительную важность или предпочтительность элементов построенной иерархической структуры, с помощью процедуры парных сравнений. Безразмерные приоритеты позволяют обоснованно сравнивать разнородные факторы, что является отличительной особенностью МАИ. На заключительном этапе анализа выполняется синтез (линейная свёртка) приоритетов на иерархии, в результате которой вычисляются приоритеты альтернативных решений относительно главной цели. Лучшей считается альтернатива с максимальным значением приоритета.

Пример задачи многокритериального выбора с простейшей иерархией

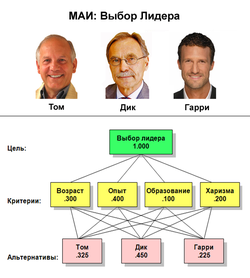
В данной задаче необходимо выбрать из трех кандидатов одного на должность руководителя (см. рисунок). Кандидаты оцениваются по критериям: возраст, опыт, образование и личные качества. На рисунке показана иерархия для этой задачи. Простейшая иерархия содержит три уровня: цель, критерии и альтернативы. Числа на рисунке показывают приоритеты элементов иерархии с точки зрения цели, которые вычисляются в МАИ на основе парных сравнений элементов каждого уровня относительно связанных с ними элементами вышерасположенного уровня. Приоритеты альтернатив относительно цели (глобальные приоритеты) вычисляются на заключительном этапе метода путём линейной свёртки локальных приоритетов всех элементов. В данном примере лучшим кандидатом является Дик, так как имеет максимальное значение глобального приоритета

Сфера образования и научных исследований

Хотя для практического применения МАИ отсутствует необходимость специальной подготовки, основы метода преподают во многих учебных заведениях . Кроме того, этот метод широко применяется в сфере управления качеством и читается в рамках многих специализированных программ, таких как Six Sigma, Lean Six Sigma, и QFD .

Около ста китайских университетов предлагают курсы по основам МАИ, и многие соискатели научных степеней выбирают МАИ в качестве объекта научных и диссертационных исследований. Опубликовано более 900 научных статей по данной тематике. Существует китайский научный журнал, специализирующийся в области МАИ .

Раз в два года проводится Международный симпозиум, посвященный МАИ (International Symposium on Analytic Hierarchy Process, ISAHP), на котором встречаются как ученые, так и практики, работающие с МАИ. В 2007 году симпозиум проходил в Вальпараисо, Чили, где было представлено более 90 докладов ученых из 19 стран, включая США, Германию, Японию, Чили, Малайзию, и Непал .

Методика применения МАИ

Метод анализа иерархий содержит процедуру синтеза приоритетов, вычисляемых на основе субъективных суждений экспертов. Число суждений может измеряться дюжинами или даже сотнями. Математические вычисления для задач небольшой размерности можно выполнить вручную или с помощью калькулятора, однако гораздо удобнее использовать программное обеспечение (ПО) для ввода и обработки суждений. Самый простой способ компьютерной поддержки — электронные таблицы, самое развитое ПО предусматривает применение специальных устройств для ввода суждений участниками процесса коллективного выбора.

Порядок применения МАИ:

1. Построение качественной модели проблемы в виде иерархии, включающей цель, альтернативные варианты достижения цели и критерии для оценки качества альтернатив;
2. Определение приоритетов всех элементов иерархии с использованием метода парных сравнений;
3. Синтез глобальных приоритетов альтернатив путём линейной свёртки приоритетов элементов на иерархии;
4. Проверка суждений на согласованность;
5. Принятие решения на основе полученных результатов .

Рассмотрим эти шаги подробнее.

Моделирование проблемы в виде иерархии

Первый шаг МАИ — построение иерархической структуры, объединяющей цель выбора, критерии, альтернативы и другие факторы, влияющие на выбор решения. Построение такой структуры помогает проанализировать все аспекты проблемы и глубже вникнуть в суть задачи.

Определение иерархической структуры

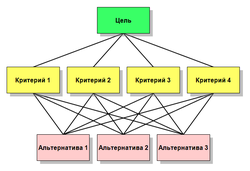
Иерархическая структура — это графическое представление проблемы в виде перевёрнутого дерева, где каждый элемент, за исключением самого верхнего, зависит от одного или более выше расположенных элементов. Часто в различных организациях распределение полномочий, руководство и эффективные коммуникации между сотрудниками организованы в иерархической форме.

Иерархические структуры используются для лучшего понимания сложной реальности: мы раскладываем исследуемую проблему на составные части; затем разбиваем на составные части получившиеся элементы и т.д. На каждом шаге важно фокусировать внимание на понимании текущего элемента, временно абстрагируясь от всех прочих компонентов. При проведении подобного анализа приходит понимание всей сложности и многогранности исследуемого предмета.

В качестве примера можно привести иерархическую структуру, которая используется при обучении в медицинских вузах . В рамках изучения анатомии отдельно рассматривается костно-мышечная система (которая включает такие элементы, как руки и их составляющие: мышцы и кости), сердечно-сосудистая система (и её множественные уровни), нервная система (и её компоненты и подсистемы) и т.д. Степень детализации доходит до клеточного и молекулярного уровня. В конце изучения приходит понимание системы организма в целом, а также осознание того, какую роль в нем занимает каждая часть. С помощью подобного иерархического структурирования студенты приобретают всесторонние знания об анатомии.

Аналогичным образом, когда мы решаем сложную проблему, мы можем использовать иерархию как инструмент для обработки и восприятия больших объёмов информации. По мере проектирования этой структуры формируется всё более полное понимание проблемы .

Объяснение иерархических структур, используемых в МАИ

Иерархические структуры, используемые в МАИ, представляют собой инструмент для качественного моделирования сложных проблем. Вершиной иерархии является главная цель; элементы нижнего уровня представляют множество вариантов достижения цели (альтернатив); элементы промежуточных уровней соответствуют критериям или факторам, которые связывают цель с альтернативами.

Существуют специальные термины для описания иерархической структуры МАИ. Каждый уровень состоит из узлов. Элементы, исходящие из узла, принято называть его детьми (дочерними элементами). Элементы, из которых исходит узел, называются родительскими. Группы элементов, имеющие один и тот же родительский элемент, называются группами сравнения. Родительские элементы альтернатив, как правило, исходящие из различных групп сравнения, называются покрывающими критериями. Используя эти термины для описания представленной ниже диаграммы, можно сказать, что четыре критерия — это дети цели; в свою очередь, цель — это родительский элемент для любого из критериев. Каждая Альтернатива — это дочерний элемент, каждого из включающих её критериев. Всего на диаграмме присутствует две группы сравнения: группа, состоящая из четырех критериев и группа, включающая три Альтернативы.

Вид любой иерархии МАИ будет зависеть не только от объективного характера рассматриваемой проблемы, но и от знаний, суждений, системы ценностей, мнений, желаний и т.п. участников процесса. Опубликованные описания применений МАИ часто включают в себя различные схемы и объяснения представленных иерархий . Последовательное выполнение всех шагов МАИ предусматривает возможность изменения структуры иерархии, с целью включения в неё вновь появившихся, или ранее не считавшихся важными, критериев и Альтернатив .

Расстановка приоритетов

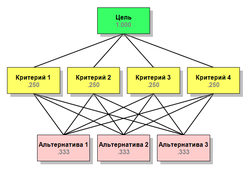
После построения иерархии участники процесса используют МАИ для определения приоритетов всех узлов структуры. Информация для расстановки приоритетов собирается со всех участников и математически обрабатывается. В данном разделе приведена информация, на простом примере поясняющая процесс вычисления приоритетов.

Определение приоритетов и пояснения

Приоритеты — это числа, которые связаны с узлами иерархии. Они представляют собой относительные веса элементов в каждой группе. Приоритеты — безразмерные величины, подобно вероятностям, которые могут принимать значения от нуля до единицы. Чем больше величина приоритета, тем более значимым является соответствующий ему элемент. Сумма приоритетов элементов, подчиненных одному элементу выше лежащего уровня иерархии, равна единице. Приоритет цели по определению равен 1.0. Рассмотрим простой пример, поясняющий методику вычисления приоритетов.

На рисунке показана иерархия, в которой приоритеты всех элементов не устанавливались ЛПР. В таком случае по умолчанию приоритеты элементов считаются одинаковыми, то есть все четыре критерия имеют равную важность с точки зрения цели, а приоритеты всех альтернатив равны по всем критериями. Другими словами, альтернативы в этом примере неразличимы. Заметим, что сумма приоритетов элементов любого уровня, равна единице. Если бы альтернатив было две, то их приоритеты были бы равны 0.500, если бы критериев было 5, то приоритет каждого был бы равен 0.200. В этом простом примере приоритеты альтернатив по разным критериям могут не совпадать, что обычно и бывает на практике.

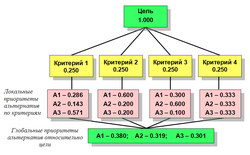
Приведем пример, в котором локальные приоритеты альтернатив по разным критериям не совпадают. Глобальные приоритеты альтернатив относительно цели вычисляются путём умножения локального приоритета каждой альтернативы на приоритет каждого критерия и суммирования по всем критериям.

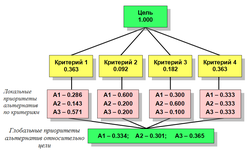
Если приоритеты критериев изменятся, то изменятся значения глобальных приоритетов альтернатив, следовательно, может измениться их порядок. На рисунке показано решение данной задачи с изменившимися значениями приоритетов критериев, при этом наиболее предпочтительной альтернативой становится A3.

См.также

• Аналитический иерархический процесс
• Программное обеспечение для принятия решений

Примечания

Литература

• Саати Т. Л. Об измерении неосязаемого. Подход к относительным измерениям на основе главного собственного вектора матрицы парных сравнений // Журнал "Cloud Of Science". 2015. Т. 2. № 1.( от 15 марта 2016 на Wayback Machine )
• Саати Т. Л. Относительное измерение и его обобщение в принятии решений. Почему парные сравнения являются ключевыми в математике для измерения неосязаемых факторов // Cloud Of Science". 2016. Т. 3. № 2. C. 171-262 ( от 22 апреля 2018 на Wayback Machine )
• Саати Т. Л. Принятие решений при зависимостях и обратных связях: Аналитические сети. — М.: Издательство ЛКИ, 2008. — 360 с.
• Саати Т. Л. Целочисленные методы оптимизации и связанные с ними экстремальные проблемы. — М.: Мир, 1973. — 302 с.
• Басакер Р. Г., Саати Т. Л. Конечные графы и сети. — М.: Наука, 1974. — 366с.
• Саати Т. Л. Принятие решений. Метод анализа иерархий. — М.: Радио и связь, 1989. — 316 с.
• Саати Т., Кернс К. Аналитическое планирование. Организация систем. — М.: Радио и связь, 1991. — 224 с.
• Андрейчиков А. В., Андрейчикова О. Н. Анализ, синтез, планирование решений в экономике. — М.: Финансы и статистика, 2004. — 464 с.
• Абакаров А.Ш., Сушков Ю.А. // Электронный научный журнал "Исследовано в России", 2005. 2130-2146.