Interested Article - Тасование Фишера — Йетса
- 2021-12-24
- 1
Тасование Фишера — Йетса (названо в честь Рональда Фишера и Фрэнка Йейтса , известно также под именем Тасование Кнута (в честь Дональда Кнута ), — это алгоритм создания случайных перестановок конечного множества , попросту говоря, для случайного тасования множества. Вариант тасования Фишера — Йетса, известный как алгоритм Саттоло (Sattolo) , может быть использован для генерации случайного цикла перестановок длины n . Правильно реализованный алгоритм тасования Фишера — Йетса несмещённый , так что каждая перестановка генерируется с одинаковой вероятностью. Современная версия алгоритма очень эффективна и требует время, пропорциональное числу элементов множества, и не требует дополнительной памяти.
Основная процедура тасования Фишера — Йетса аналогична случайному вытаскиванию записок с числами из шляпы или карт из колоды, один элемент за другим, пока элементы не кончатся. Алгоритм обеспечивает эффективный и строгий метод таких операций, гарантирующий несмещённый результат.
Оригинальный метод Фишера — Йетса
Тасование Фишера — Йетса, в его первоначальном виде, было описано в 1938 году Рональдом Фишером и Фрэнком Йетсом в их книге Статистические таблицы для исследований в области биологии, архитектуры и медицины (Последнее издание книги описывает другой алгоритм тасования, приписываемый К. Р. Рао .) Их метод был разработан для карандаша и бумаги и использовал вычисленные заранее таблицы случайных чисел как источник случайности. Выглядел он следующим образом:
- Запишем числа от 1 до N .
- Выберем случайное число k в диапазоне { 1, D }, где D - число оставшихся чисел. Числа 1 и D включаются.
- Вычеркиваем k -е оставшееся число, отсчитывая числа в порядке возрастания, и записываем его где-нибудь.
- Повторяем шаг 2, пока все числа не будут выбраны.
- Последовательность чисел, записанных на шаге 3, является случайной перестановкой.
Если числа, используемые на шаге 2, действительно случайны и не смещены, мы получим такими же и случайные перестановки (случайны и не смещены). Фишер и Йетс описали, каким образом получить такие случайные числа для любого интервала, и предоставили таблицы, позволяющие избежать смещения. Они также предполагали возможность упростить метод — выбирать случайные числа от единицы до N , и, затем, отбрасывать повторения — для генерации половины генерируемой перестановки, и только потом использовать более сложный алгоритм для оставшейся половины, в противном случае повторяющиеся числа будут попадаться слишком часто.
Современный алгоритм
Современный вариант алгоритма тасования Фишера — Йетса, предназначенный для использования в компьютерах, был представлен Ричардом Дурштенфельдом (Richard Durstenfeld) в 1964-м году в журнале Communications of the ACM том 7, выпуск 7, под названием «Algorithm 235: Random permutation» , и был популяризован Дональдом Кнутом во втором томе его книги « Искусство программирования » как «Алгоритм P» . Ни Дурштенфельд, ни Кнут в первом издании книги не упомянули об алгоритме Фишера и Йетса, и, похоже, не были осведомлены о нём. Во втором издании книги «Искусство программирования», однако, это упущение было исправлено
Алгоритм, описанный Дурштенфельдом, отличается от алгоритма Фишера и Йетса в небольших, но существенных деталях. Чтобы компьютерная реализация алгоритма не тратила бесполезно время на перебор оставшихся чисел на шаге 3, у Дурштенфельда на каждой итерации выбираемые числа переносились в конец списка путём перестановки с последним невыбранным числом. Эта модификация сокращала временную сложность алгоритма до O ( n ), по сравнению с O ( n 2 ) для исходного алгоритма . Это изменение приводит к следующему алгоритму.
Для тасования массива a из n элементов (индексы 0..n-1):
для всех i от n − 1 до 1 выполнить
j ← случайное число 0 ≤ j ≤ i
обменять местами a[j] и a[i]
«Вывернутый» алгоритм
Тасование Фишера — Йетса в варианте Дурштенфельда является тасованием на месте . То есть, при задании заполненного массива, он тасует элементы в том же массиве, а не создает копию массива с переставленными элементами. Это может дать существенное преимущество при тасовании больших массивов.
Одновременная инициализация и тасование массива может немного увеличить эффективность, если использовать «вывернутую» версию тасования. В этой версии исходный элемент с индексом i переносится в случайную позицию среди первых i позиций после того, как с этой позиции будет перенесен элемент на позицию i . В случае выбора случайного числа, равного i , будет сначала перенесено неприсвоенное значение, но оно будет тотчас же затерто правильным значением. Никакой отдельной инициализации в этом варианте не нужно, и никаких перестановок не осуществляется. Если источник определяется простой функцией, как, например, целые числа от 0 до n — 1 , источник может быть просто заменен этой функцией, поскольку источник никогда не меняется во время выполнения.
Для создания массива a из n случайно перетасованных элементов источника:
for i from 0 to n − 1 do
j ← random integer with 0 ≤ j ≤ i
a[i] ← a[j]
a[j] ← source[i]
Корректность «вывернутого» тасования можно доказать по индукции; любая из n ! различных последовательностей случайных чисел, получаемых во время работы алгоритма образует свою собственную перестановку, так что все перестановки будут получены только один раз.
Другое преимущество этого подхода состоит в том, что, даже не зная числа «n», числа элементов источника , мы можем создавать равномерно распределенные перестановки. Ниже массив a создается итеративно, начиная с пустого и a .length представляет его текущую длину.
пока источник.естьЕще
j ← случайное число 0 ≤ j ≤ a.length
если j = a.length
a.добавить(источник.следующийЭлемент)
в противном случае
a.добавить(a[j])
a[j] ← источник.следующийЭлемент
Примеры
С карандашом и бумагой
В качестве примера, переставим числа от 1 до 8, используя . Для начала выпишем числа на бумаге:
| Интервал | Выбрано | Черновик | Результат |
|---|---|---|---|
| 1 2 3 4 5 6 7 8 |
Теперь возьмем случайное число k от 1 до 8 — пусть это будет 3 — и вычеркнем k -е (то есть третье) число (3, конечно) и переносим его в результирующую последовательность:
| Интервал | Выбрано | Черновик | Результат |
|---|---|---|---|
| 1-8 | 3 |
1 2
|
3 |
Теперь выбираем второе случайное число, на этот раз из интервала 1—7, пусть это будет 4. Теперь вычеркиваем четвёртое ещё не вычеркнутое число из черновика — это будет число 5 — и добавим его в результат:
| Интервал | Выбрано | Черновик | Результат |
|---|---|---|---|
| 1-7 | 4 |
1 2
|
3 5 |
Теперь мы выбираем случайное число из интервала 1—6, затем из интервала 1—5, и так далее, повторяя процесс вычеркивания, как описано выше:
| Интервал | Выбрано | Черновик | Результат |
|---|---|---|---|
| 1-6 | 5 |
1 2
|
3 5 7 |
| 1-5 | 3 |
1 2
|
3 5 7 4 |
| 1-4 | 4 |
1 2
|
3 5 7 4 8 |
| 1-3 | 1 |
|
3 5 7 4 8 1 |
| 1-2 | 2 |
|
3 5 7 4 8 1 6 |
|
|
3 5 7 4 8 1 6 2 |
Современный метод
Сделаем то же самое с помощью . На этот раз, вместо вычеркивания выбранных чисел и копирования их куда-либо, мы переставляем их с ещё не выбранными числами. Как и раньше, начнем с выписывания чисел от 1 до 8:
| Интервал | Выбрано | Черновик | Результат |
|---|---|---|---|
| 1 2 3 4 5 6 7 8 |
Выберем первое случайное число от 1 до 8, пусть это будет 6, так что переставляем местами 6-е и 8-е числа в списке:
| Интервал | Выбрано | Черновик | Результат |
|---|---|---|---|
| 1-8 | 6 | 1 2 3 4 5 8 7 | 6 |
Следующее случайное число мы выбираем из интервала 1 — 7, и пусть это будет 2. Теперь мы переставляем 2-е и 7-е числа:
| Интервал | Выбрано | Черновик | Результат |
|---|---|---|---|
| 1-7 | 2 | 1 7 3 4 5 8 | 2 6 |
Следующее случайное число мы выбираем из интервала 1 — 6, и пусть это будет 6, что означает, что нам следует оставить 6-е число на месте (после предыдущих перестановок здесь стоит число 8). Продолжаем действовать таким образом, пока вся перестановка не будет сформирована:
| Интервал | Выбрано | Черновик | Результат |
|---|---|---|---|
| 1-6 | 6 | 1 7 3 4 5 | 8 2 6 |
| 1-5 | 1 | 5 7 3 4 | 1 8 2 6 |
| 1-4 | 3 | 5 7 4 | 3 1 8 2 6 |
| 1-3 | 3 | 5 7 | 4 3 1 8 2 6 |
| 1-2 | 1 | 7 | 5 4 3 1 8 2 6 |
Варианты
Алгоритм Саттоло
Очень похожий алгоритм был опубликован в 1986 году Сандрой Саттоло (Sandra Sattolo) для генерации равномерно распределенных циклов (максимальной) длины n Разница между алгоритмами Дурштенфельда и Саттоло заключается лишь в шаге 2 — в алгоритме Саттоло случайное число j выбирается из интервала 1 — i −1, а не из 1 — i . Эта простая модификация приводит к перестановкам, состоящим из одного цикла.
Фактически, как описано ниже, легко случайно реализовать алгоритм Саттоло при попытке создать алгоритм Фишера — Йетса. Такая ошибка приводит к генерации перестановок из меньшего множества ( n −1)! циклов длины N , вместо полного множества из n ! возможных перестановок.
То, что алгоритм Саттоло всегда создает цикл длины n , может быть показано по индукции. Предположим, что после первой итерации (переставившей элемент n на позицию k < n ) остальные n − 1 итераций образовали цикл элементов длиной n − 1. Проследим цепочку перемещений — возьмем какой-либо элемент, он переместится на некоторую позицию p , вытеснив элемент, находившийся там, на некоторую новую позицию, и так далее. По принятому предположению мы попадем на начальную позицию, только перебрав все остальные позиции. Последний элемент, после перемещения на позицию k , и последовательных перестановок первых n − 1 элементов попадет на позицию l ; сравним перестановку π всех n элементов с перестановкой σ первых n − 1 элементов. Отслеживая перестановки, как было упомянуто выше, мы не найдем разницу между π и σ , пока не достигнем позиции k . В π элемент, находящийся на позиции k , переместится на последнюю позицию, а не на позицию l , а элемент, находящийся на последней позиции, попадет на место l . Начиная с этого места последовательность перемещений элементов π снова будет совпадать с σ , и все позиции будут пройдены перед возвратом на начальную позицию, что и требовалось.
Как и в случае доказательства равновероятности перестановок, нам достаточно показать, что алгоритм Саттоло создает ( n −1)! различных перестановок, которые, ввиду предполагаемой несмещенности генератора случайных чисел, имеют равную вероятность. ( n −1)! различных перестановок, генерируемых алгоритмом, в точности покрывают множество циклов длины n .
Простая реализация алгоритма Саттоло на языке Python :
from random import randrange
def sattoloCycle(items):
i = len(items)
while i > 1:
i = i - 1
j = randrange(i) # 0 <= j <= i-1
items[j], items[i] = items[i], items[j]
return
Сравнение с другими алгоритмами тасования
Алгоритм Фишера — Йетса вполне эффективен, и даже более того, его скорость и затраты памяти асимптотически оптимальны. При использовании высококачественного несмещенного генератора случайных чисел алгоритм гарантирует несмещенный результат. У алгоритма существует ещё одно преимущество — если требуется получить некоторую часть перестановок, алгоритм может быть остановлен на полпути или даже остановлен и возобновлен многократно.
Существует альтернативный метод — каждому элементу множества присваивается случайное число, а затем множество сортируется согласно присвоенным числам. Асимптотическая оценка скорости сортировки в лучшем случае равна O ( n log n ), что несравнимо с оценкой O ( n ) скорости работы алгоритма Фишера — Йетса. Как и тасование Фишера — Йетса, сортирующий метод дает несмещенные перестановки, но он менее чувствителен к возможным проблемам генератора случайных чисел. Однако следует уделить особое внимание генерации случайных чисел, чтобы избежать повторения, поскольку алгоритм с сортировкой, в общем случае, не сортирует элементы случайно.
Существует вариант метода с сортировкой, в котором список сортируется с использованием функции сравнения, возвращающей случайное число. Однако это исключительно плохой метод : он с большой вероятностью образует неравномерное распределение, вдобавок зависящее от метода используемой сортировки . Например, при использовании быстрой сортировки , с фиксированным элементом, используемым в качестве начального элемента. Этот алгоритм сортировки сравнивает остальные элементы списка с выбранным (меньше или больше его) и таким способом определяется результирующее положение элемента. Если сравнение будет возвращать «меньше» и «больше» с равной вероятностью, то выбранный элемент окажется в центре с куда большей вероятностью, чем на концах. Другой метод сортировки, подобный сортировке слиянием , может создавать перестановки с более равномерной вероятностью, но, все же имеет недостатки, поскольку слияние двух последовательностей со случайным выбором последовательности с одинаковой вероятностью (пока не исчерпаем последовательность случайных чисел) не создает результат с равномерным распределением вероятности, поскольку вероятность выбрать последовательность должна быть пропорциональна числу элементов последовательности. Фактически никакой метод, использующий «бросание монеты», то есть последовательный выбор из двух возможностей, не может создать перестановки (из более чем двух элементов) с равномерным распределением, поскольку любое событие при этой схеме имеет вероятность в виде рациональной дроби с делителем, равным степени двойки, в то время как требуемая вероятность должна быть 1/ n !.
В принципе, такие методы тасования могут привести к зацикливанию алгоритма или ошибке доступа к памяти, поскольку корректность алгоритма сортировки может зависеть от свойств упорядочения, таких как транзитивность . Хотя такого рода поведение не должно случаться в сортировках, в которых сравнение нельзя предсказать по предыдущим сравнениям, иногда имеются причины для таких сравнений. Например, тот факт, что элемент должен быть равен всегда самому себе, в целях эффективности, может использоваться как некоторый признак или флаг, а это при случайных сравнения нарушает алгоритм сортировки.
Потенциальные источники неравномерности распределения
Следует проявлять осторожность при реализации алгоритма Фишера — Йетса, как в части самого алгоритма, так и для генератора случайных чисел, на котором он базируется. Некоторые общие ошибки реализации приведены ниже.
Ошибки при реализации алгоритма
Общей ошибкой при реализации тасования Фишера — Йетса является выбор случайных чисел из неверного интервала . Дефектный алгоритм может казаться работающим корректно, но он не создает все возможные перестановки с равной вероятностью, а некоторые перестановки может вообще не создать. Например, общая ошибка занижения или завышения на единицу может возникнуть при выборе индекса j переставляемого элемента в всегда меньше индекса i , с которым элемент должен быть переставлен. В результате вместо тасования Фишера — Йетса получим , который образует перестановки, затрагивающие все элементы. В частности, в этом случае никакой элемент не может оказаться на начальной позиции.
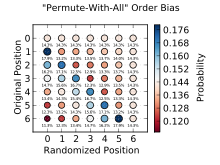
Подобным образом, выбор j из всех индексов в массиве на каждой итерации также образует неравновероятные перестановки, хотя и не столь очевидно. Это можно установить из того факта, что такая реализация образует n n различных обменов местами для элементов, в то время как существует всего n ! возможных перестановок массива из n элементов. Поскольку n n никогда не может делиться на n ! без остатка при n > 2 (поскольку n ! делится на число n −1, которое не имеет с n общих простых делителей), то некоторые перестановки должны появляться чаще, чем другие. Рассмотрим конкретный пример перестановок трех элементов [1, 2, 3]. Имеется 6 возможных перестановок этого набора (3! = 6), но алгоритм образует 27 перетасовок (3 3 = 27). В этом случае [1, 2, 3], [3, 1, 2], и [3, 2, 1] встречаются по 4 раза в 27 перетасовках, в то время как оставшиеся 3 встречаются по 5 раз.
Матрица справа показывает вероятность появления каждого элемента из списка длины 7 в конечной позиции. Заметьте, что для большинства элементов остаться при тасовании на своей начальной позиции (главная диагональ матрицы) имеет минимальную вероятность, а сдвинуться на одну позицию влево — максимальную.
Нарушение равномерности распределения при взятии по модулю
Алгоритм Фишера — Йетса использует выборку равномерно распределенных случайных чисел из различных диапазонов. Большинство генераторов случайных чисел , однако, как настоящих случайных, так и псевдослучайных дают числа в фиксированном диапазоне, скажем, от 0 до 2 32 −1. Простой и обычно используемый метод приведения таких чисел к нужному интервалу заключается в использовании взятия остатка от деления на верхнюю границу. Необходимость генерировать случайные числа во всех интервалах от 0-1 до 0- n гарантирует, что некоторые из этих границ не будут делить естественную границу генератора нацело. Как результат распределение не будет равномерным и маленькие остатки будут встречаться чаще.
Предположим, например, что генератор дает случайные числа между 0 и 99 (как было у Фишера и Йетса в их оригинальных таблицах), а вы хотите получить случайные числа между 0 и 15. Если вы просто находите остаток числа при делении на 16, вы обнаружите, что числа 0-3 встречаются на 17 % чаще, чем остальные. Причина этого заключается в том, что 16 не делит 100 нацело — наибольшее число, кратное 16 и не превышающее 100 есть 6×16 = 96, а оставшиеся числа из диапазона 96-99 создают неравномерность. Самый простой способ избежать этой проблемы заключается в отбрасывании таких чисел до взятия остатка. Хотя, в принципе, числа из такого интервала могут попадаться, математическое ожидание числа повторных попыток всегда меньше единицы.
Похожая проблема возникает в случае использования генератора случайных чисел, дающего числа с плавающей запятой , обычно в диапазоне [0,1). Полученное число умножают на размер желаемого диапазона и округляют. Проблема здесь в том, что даже аккуратно сгенерированные случайные числа с плавающей запятой имеют конечную точность, что означает, что можно получить только конечное число возможных чисел с плавающей запятой, и, как и в случае выше, эти числа разбиваются на сегменты, которые не делят число нацело и некоторые сегменты получают большую вероятность появления, чем другие.
Псевдослучайные генераторы: проблемы, обусловленные внутренними состояниями генератора случайных чисел, начальными параметрами и использованием
Дополнительные проблемы появляются при использовании генератора псевдослучайных чисел (ГПСЧ). Генерация псевдослучайной последовательности таких генераторов полностью определяется их внутренним состоянием в начале генерации. Программа тасования, опирающаяся на такой генератор, не может создать больше перестановок, чем число внутренних состояний генератора. Даже когда число возможных состояний генератора перекрывает число перестановок, некоторые перестановки могут появляться чаще, чем другие. Во избежание появления неравномерности распределения число внутренних состояний генератора случайных чисел должно превосходить число перестановок на несколько порядков.
Например, встроенный генератор псевдослучайных чисел, имеющийся во многих языках программирования и библиотеках, использует, обычно, 32-битное число для внутренних состояний, что означает, что такой генератор может создать только 2 32 различных случайных чисел. Если такой генератор будет использоваться для тасования колоды из 52 игральных карт , он может создать очень маленькую часть от 52! ≈ 2 225.6 возможных перестановок. Генератор с менее чем 226-битным числом внутренних состояний не может создать все перестановки колоды из 52 игральных карт. Считается, что для создания равномерного распределения необходим генератор, имеющий не менее 250-битного числа состояний.
Естественно, что никакой генератор псевдослучайных чисел не может создать больше случайных последовательностей, задающихся различными начальными данными, чем число этих начальных данных. Так, генератор с 1024-битным числом внутренних состояний, для которого задаются 32-битные начальные параметры, может создать лишь 2 32 различных последовательностей перестановок. Можно получить больше перестановок, выбирая достаточно много случайных чисел из генератора до начала его использования в алгоритме тасования, но такой подход очень неэффективен — выборка, скажем, 2 30 случайных чисел до использования последовательности в алгоритме тасования повышает число перестановок только до 2 62 .
Ещё одна проблема появляется при использовании простого линейного конгруэнтного ГПСЧ, когда для уменьшения интервала случайных чисел используется остаток от деления, как было указано выше. Проблема здесь в том, что младшие биты линейного конгруэнтного ГПСЧ менее случайны по сравнению со старшими битами — младшие n бит имеют период максимум 2 n . Если делитель является степенью двойки, взятие остатка означает отбрасывание старших битов, что приводит к существенному уменьшению случайности.
Наконец, следует заметить, что даже использование прекрасного генератора, изъян в алгоритме может возникнуть из-за неправильного использования генератора. Представим себе, например, что реализация алгоритма на языке Java создает новый генератор для каждого вызова процесса тасования без задания параметров в конструкторе. Для инициализации генератора будет использовано текущее время (System.currentTimeMillis()). Таким образом, два вызова с разницей во времени менее миллисекунды дадут идентичные перестановки. Это случится почти наверняка, если тасование происходит многократно и быстро, что приведет к крайне неравномерному распределению перестановок. Такая же проблема может возникнуть при получении случайных чисел из двух различных потоков. Правильнее использовать один статический экземпляр генератора, определенный вне процедуры тасования.
См. также
- RC4 , a stream cipher based on shuffling an array
- Reservoir sampling , in particular Algorithm R which is a specialization of the Fisher-Yates shuffle
Примечания
- Fisher, R.A.; Yates, F. Statistical tables for biological, agricultural and medical research (англ.) . — 3rd. — London: Oliver & Boyd, 1948. — P. 26—27. . (Замечание: шестое издание, ISBN 0-02-844720-4 , от 23 октября 2009 на Wayback Machine , но оно дает другой алгоритм тасования — алгоритм C. R. Rao)
- Durstenfeld, Richard (July 1964). «Algorithm 235: Random permutation». Communications of the ACM 7 (7): 420.
- Knuth, Donald E. The Art of Computer Programming volume 2: Seminumerical algorithms (англ.) . — Reading, MA: Addison–Wesley , 1969. — P. 124—125.
- Knuth. The Art of Computer Programming vol. 2 (неопр.) . — 3rd. — Boston: Addison–Wesley , 1998. — С. 145—146. — ISBN 0-201-89684-2 .
- Black, Paul E. . Dictionary of Algorithms and Data Structures . National Institute of Standards and Technology (19 декабря 2005). Дата обращения: 9 августа 2007. 4 июня 2013 года.
-
Wilson, Mark C. (2004-06-21).
(PDF)
. In F. Chyzak (ed.) (ed.).
INRIA Research Report
.
. Vol. 5542. summary by Éric Fusy. pp. 105—108.
ISSN
.
(PDF)
из оригинала
21 июля 2011
. Дата обращения:
3 июня 2013
.
{{ cite conference }}:|editor=имеет универсальное имя ( справка ) . - . require ‘brain’ (19 июня 2007). Дата обращения: 9 августа 2007. 4 июня 2013 года.
- . Rob Weir: An Antic Disposition (27 февраля 2010). Дата обращения: 28 февраля 2010. 4 июня 2013 года.
- . require ‘brain’ (8 мая 2009). Дата обращения: 8 мая 2009. 4 июня 2013 года.
- Jeff Atwood. . (7 декабря 2007). Дата обращения: 3 июня 2013. 4 июня 2013 года.
Ссылки
- Mike Bostock. (14 января 2012). — Интерактивный пример.
- 2021-12-24
- 1



















