Степенна́я фу́нкция — функция ${\displaystyle y=x^{a}}$ , где ${\displaystyle a}$ ( показатель степени ) — некоторое вещественное число . К степенным часто относят и функцию вида ${\displaystyle y=kx^{a}}$ , где ${\displaystyle k}$ — некоторый (ненулевой) коэффициент . Существует также комплексное обобщение степенной функции .

Степенная функция является частным случаем многочлена . На практике показатель степени почти всегда является целым или рациональным числом .

Вещественная функция

Область определения

Для целых положительных показателей ${\displaystyle a}$ степенную функцию можно рассматривать на всей числовой прямой , тогда как для отрицательных ${\displaystyle a}$ , функция не определена в нуле (нуль является её особой точкой ) .

Для рациональных ${\displaystyle a={\frac {p}{q}}\ (q>0)}$ область определения зависит от чётности ${\displaystyle q}$ и от знака ${\displaystyle p.}$ так как ${\displaystyle x^{a}={\sqrt[{q}]{x^{p}}}.}$ :

• Если ${\displaystyle q}$ нечётно и ${\displaystyle p>0}$ , то ${\displaystyle x^{p/q}}$ определён на всей числовой прямой.
• Если ${\displaystyle q}$ нечётно и ${\displaystyle p<0}$ , то ${\displaystyle x^{p/q}}$ определён на всей числовой прямой, кроме нуля.
• Если ${\displaystyle q}$ чётно и ${\displaystyle p>0}$ , то ${\displaystyle x^{p/q}}$ определён при неотрицательных ${\displaystyle x.}$
• Если ${\displaystyle q}$ чётно и ${\displaystyle p<0}$ , то ${\displaystyle x^{p/q}}$ определён при положительных ${\displaystyle x.}$

Для вещественного показателя ${\displaystyle a}$ степенная функция ${\displaystyle x^{a}}$ , вообще говоря, определена только при ${\displaystyle x>0.}$ Если ${\displaystyle a>0,}$ то функция определена и в нуле .

Целочисленный показатель степени

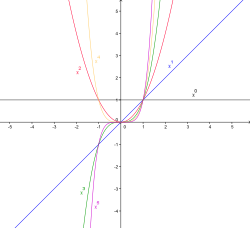
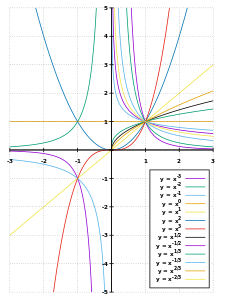
Графики степенной функции ${\displaystyle y=x^{n}}$ при целочисленном показателе ${\displaystyle n}$ :

• 
  Параболы порядка n : ${\displaystyle n=0}$ ${\displaystyle n=1}$ ${\displaystyle n=2}$ ${\displaystyle n=3}$ ${\displaystyle n=4}$ ${\displaystyle n=5}$
• 
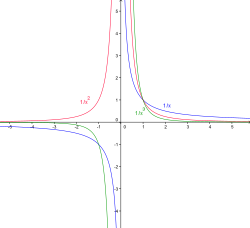
  Гиперболы порядка n : ${\displaystyle n=-1}$ ${\displaystyle n=-2}$ ${\displaystyle n=-3}$

При нечётном ${\displaystyle n}$ графики центрально-симметричны относительно начала координат , в котором имеет точку перегиба . При чётном ${\displaystyle n}$ степенная функция чётна : ${\displaystyle (-x)^{n}=x^{n},}$ её график симметричен относительно оси ординат .

Графики степенной функции при натуральном показателе ${\displaystyle n>1}$ называются параболами порядка ${\displaystyle n}$ . При чётном ${\displaystyle n}$ функция всюду неотрицательна (см. графики). При ${\displaystyle n=1}$ получается функция ${\displaystyle y=kx}$ , называемая линейной функцией или прямой пропорциональной зависимостью .

Графики функций вида ${\displaystyle y=x^{-n}={\frac {1}{x^{n}}}}$ , где ${\displaystyle n}$ — натуральное число, называются гиперболами порядка ${\displaystyle n}$ . При нечётном ${\displaystyle n}$ оси координат являются асимптотами гипербол. При чётном ${\displaystyle n}$ асимптотами являются ось абсцисс и положительное направление оси ординат (см. графики) . При показателе ${\displaystyle -1}$ получается функция ${\displaystyle y={\frac {k}{x}}}$ , называемая обратной пропорциональной зависимостью .

При ${\displaystyle a=0}$ функция вырождается в константу: ${\displaystyle y=1.}$

Рациональный показатель степени

• 
  Графики степенных функций с рациональным показателем
• 
  Полукубические параболы ${\displaystyle y=ax^{3/2}}$

Возведение в рациональную степень ${\displaystyle p/q}$ определяется формулой:

${\displaystyle x^{p/q}={\sqrt[{q}]{x^{p}}}.}$

Если ${\displaystyle p=1}$ , то функция представляет собой арифметический корень степени ${\displaystyle q}$ :

${\displaystyle y=x^{1/q}={\sqrt[{q}]{x}}.}$

Пример : из третьего закона Кеплера непосредственно вытекает, что период ${\displaystyle T}$ обращения планеты вокруг Солнца связан с большой полуосью ${\displaystyle A}$ её орбиты соотношением: ${\displaystyle T=kA^{3/2}}$ ( полукубическая парабола ).

Свойства

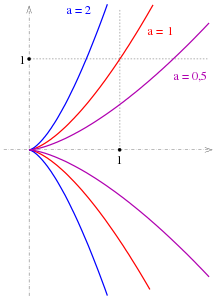
Монотонность

В интервале ${\displaystyle (0,\infty )}$ функция монотонно возрастает при ${\displaystyle a>0}$ и монотонно убывает при ${\displaystyle a<0.}$ Значения функции в этом интервале положительны .

Аналитические свойства

Функция непрерывна и неограниченно дифференцируема во всех точках, в окрестности которых она определена .

Производная функции : ${\displaystyle \left(x^{a}\right)^{\prime }=ax^{a-1}}$ .

Ноль, вообще говоря, является особой точкой. Так, если ${\displaystyle a<n}$ , то ${\displaystyle n}$ -я производная в нуле не определена. Например, функция ${\displaystyle y={\sqrt {x}}=x^{1/2}}$ определена в нуле и в его правой окрестности, но её производная ${\displaystyle y={\frac {1}{2{\sqrt {x}}}}}$ в нуле не определена.

Неопределённый интеграл :

• Если ${\displaystyle a\neq -1}$ , то ${\displaystyle \int x^{a}dx={\frac {x^{a+1}}{a+1}}+C}$
• При ${\displaystyle a=-1}$ получаем: ${\displaystyle \int {\frac {1}{x}}dx=\ln |x|+C}$

Таблица значений малых степеней

Комплексная функция

Степенная функция комплексного переменного ${\displaystyle z}$ в общем виде определяется формулой :

${\displaystyle y=z^{c}=e^{c\cdot \operatorname {Ln} (z)}}$

Здесь показатель степени ${\displaystyle c}$ — некоторое комплексное число. Значение функции, соответствующее главному значению логарифма , называется главным значением степени. Например, значение ${\displaystyle i^{i}}$ равно ${\displaystyle e^{-(4k+1){\frac {\pi }{2}}},}$ где ${\displaystyle k}$ — произвольное целое, а его главное значение есть ${\displaystyle e^{i\ln(i)}=e^{-{\frac {\pi }{2}}}.}$

Комплексная степенная функция обладает значительными отличиями от своего вещественного аналога. В силу многозначности комплексного логарифма она, вообще говоря, также имеет бесконечно много значений. Однако два практически важных случая рассматриваются отдельно.

1. При натуральном показателе степени функция ${\displaystyle y=z^{n}}$ однозначна и n -листна .
2. Если показатель степени — положительное рациональное число , то есть (несократимая) дробь ${\displaystyle {\frac {p}{q}}}$ , то у функции будет ${\displaystyle q}$ различных значений .

См. также

• Логарифм
• Целая рациональная функция
• Показательная функция
• Степенной закон в статистике

Примечания

Литература

• Битюцков В. И. Степенная функция // Математическая энциклопедия (в 5 томах). — М. : Советская Энциклопедия , 1985. — Т. 5. — С. 208—209. — 1248 с.
• Степенная функция // . — М. : Советская энциклопедия, 1988. — С. —565. — 847 с.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, в трёх томах. — изд. 6-е. — М. : Наука, 1966.

Ссылки

• // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов . — М. : Большая российская энциклопедия, 2004—2017.