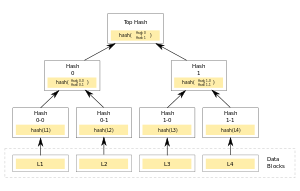
Хеш-деревом , деревом Меркла ( англ. Merkle tree ) называют полное двоичное дерево , в листовые вершины которого помещены хеши от блоков данных, а внутренние вершины содержат хеши от сложения значений в дочерних вершинах. Корневой узел дерева содержит хеш от всего набора данных, то есть хеш-дерево является однонаправленной хеш-функцией. Дерево Меркла применяется для эффективного хранения транзакций в блокчейне криптовалют (например, в Bitcoin , Ethereum ). Оно позволяет получить «отпечаток» всех транзакций в блоке, а также эффективно верифицировать транзакции .

Построение

Заполнение значений в узлах дерева идет снизу вверх. Сперва к каждому блоку данных применяется хеширование ${\displaystyle Hash_{00}=hash(L_{1})}$ , ${\displaystyle Hash_{01}=hash(L_{2})}$ и так далее. Полученные значения записываются в листья дерева. Блоки, находящиеся уровнем выше, заполняются как хеши от суммы своих детей, ${\displaystyle Hash_{0}=hash(Hash_{00}+Hash_{01})}$ , где ${\displaystyle +}$ обычно означает конкатенацию . Эта операция повторяется, пока не будет получено верхнее значение — ${\displaystyle TopHash}$ или merkle_root .

В биткойне в качестве хеш-функции используется двойное SHA-256 , то есть ${\displaystyle hash(x)=\operatorname {SHA256} (\operatorname {SHA256} (x))}$ . Впрочем, хеш-функция может быть любой, например Tiger Tree Hash (TTH), используемый в файлообменных p2p-сетях , является деревом Меркла с хеш-функцией Tiger .

Если количество блоков на каком-то уровне дерева оказывается нечетным, то один блок дублируется или переносится без изменений на следующий уровень, как это происходит при вычислении Tiger Tree Hash .

Эффективность

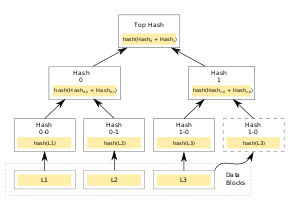
Хеш-деревья имеют преимущество перед хеш-цепочками или хеш-функциями. При использовании хеш-деревьев гораздо менее затратным является доказательство принадлежности определённого блока данных к множеству. Поскольку различными блоками часто являются независимые данные, такие как транзакции или части файлов, то нас интересует возможность проверить только один блок, не пересчитывая хеши для остальных узлов дерева. Пусть интересующий нас блок - это ${\displaystyle L_{3}}$ (см. рис.). Тогда доказательством его существования и валидности будут корневой хеш, а также верхние хеши других веток ( ${\displaystyle {auth_{L}}_{4}=Hash_{11}}$ и ${\displaystyle {auth_{L}}_{2}=Hash_{0}}$ ) . В данном случае проверка не пройдена, если ${\displaystyle TopHash\neq hash(Hash_{0}+hash(hash(L_{3})+Hash_{11}))}$ .

В общем случае можно записать

${\displaystyle signature(L)=(L\ |\ {auth_{L}}_{1},\dots ,{auth_{L}}_{K-1})}$ ,

а проверку осуществить как ${\displaystyle TopHash==Hash_{K}}$ , где

${\displaystyle Hash_{k}={\begin{cases}hash(L),&{\mbox{if }}k=1,\\hash(Hash_{k-1}+{auth_{L}}_{k-1}),&{\mbox{if }}2\leq k\leq K\end{cases}}}$ .

Набор блоков ${\displaystyle \{{auth_{L}}_{1},\dots ,{auth_{L}}_{K-1}\}}$ называется аутентификационный путь или путь Меркла .

Видно, что проверку выше можно выполнить за ${\displaystyle O(K)=O(\log _{2}N)}$ действий, где ${\displaystyle K}$ - это высота дерева или длина аутентификационного пути, а ${\displaystyle N}$ - это количество блоков данных. Такая же проверка в случае хеш-цепочки имела бы сложность ${\displaystyle O(N)}$ .

Таблица ниже демонстрирует, что даже при значительном количестве транзакций в блоке о сложности вычислений можно не беспокоиться .

Упрощенная проверка оплаты

Блок биткойна хранит только значение merkle_root своих транзакций. Это позволяет получить определённые преимущества и снизить нагрузку на сеть.

После накопления достаточного числа блоков можно удалять старые транзакции для экономии места. При этом сам блок остается неизменным, так как в нём хранится только merkle_root . Блок без транзакций занимает 80 Б, или 4,2 МБ в год (при генерации блока каждые 10 минут) .

Становится возможной упрощенная проверка оплаты ( англ. Simplified payment verification ). SPV-узел загружает не весь блок, а только заголовок блока. Для интересующей его транзакции он запрашивает также ее аутентификационный путь. Таким образом он загружает всего несколько килобайт, тогда как полный размер блока может быть больше 10 мегабайт (см. таблицу) . Использование этого метода, однако, требует, чтобы пользователь доверял узлу сети, у которого будет запрашивать заголовки блоков. Один из способов избежать атаки, то есть подмены узла недобросовестной стороной, — рассылать оповещения по всей сети при обнаружении ошибки в блоке, вынуждая пользователя загружать блок целиком .

На упрощенной проверке оплаты основана работа так называемых «тонких» биткойн-клиентов .

Дополнительно

Проблема обхода дерева Меркла

Дерево Меркла имеет также и недостатки, проявляющиеся при растущем количестве листьев. Как было показано ранее, для вычисления подписи произвольного блока ${\displaystyle L}$ нужно знать все значения из множества ${\displaystyle \{{auth_{L}}_{i}\}}$ . Это не вызывает проблем, если есть возможность хранить все внутренние вершины дерева в памяти, однако для больших деревьев (количество листьев может увеличиваться до ${\displaystyle 2^{40}}$ ) это не подходит. Можно также каждый раз вычислять внутренние блоки заново, но это значительно понизит производительность такой системы. Поэтому возникает проблема эффективного обхода дерева и генерации подписей ( англ. Merkle tree traversal problem ) . На сегодняшний день существуют решения, использующие ${\displaystyle 2\log _{2}(N)}$ времени и ${\displaystyle 3\log _{2}(N)}$ памяти, где ${\displaystyle N}$ — это количество листьев. Было также доказано, что не существует алгоритма обхода, который бы был одновременно лучше, чем ${\displaystyle O(\log _{2}(N))}$ и по времени, и по памяти .

Примечания

См. также

• Подпись Меркла
• Двоичное дерево
• Tiger (хеш-функция)
• Magnet-ссылка
• URN

Ссылки

• — улучшенная реализация дерева Меркла, использующаяся в Ethereum.
• — предложение по замене SHA-1 на Tiger Tree Hash в .torrent файлах.