Ферромагнетизм
- 1 year ago
- 0
- 0

Магнети́зм — форма взаимодействия движущихся электрических зарядов , осуществляемая на расстоянии посредством магнитного поля . Наряду с электричеством , магнетизм — одно из проявлений электромагнитного взаимодействия . С точки зрения квантовой теории поля электромагнитное взаимодействие переносится бозоном — фотоном (частицей, которую можно представить как квантовое возбуждение электромагнитного поля ).

Существуют различные сведения о первом упоминании магнитов, обычно рассматривающихся в истории Древнего мира в контексте компаса или религиозных культов. Согласно одним оценкам, магнетит или магнитный железняк впервые был открыт в Китае за четыре тысячи лет до н. э. При этом отмечается, что западным исследователям свойственно отдавать приоритет в открытии магнетизма древним грекам . Первые упоминания в летописях о применении магнитных материалов восходят к третьему тысячелетию до н. э., когда легендарный китайский император Хуан-ди использовал компас во время битвы . Однако по иной версии, он использовал так называемые колесницы, указывающие на юг . Китайские мореплаватели конца второго тысячелетия до н. э. использовали компас для морской навигации . В целом, время его изобретения оценивается между 2637 и 1100 годами до н. э. Компас в виде ложки на гладкой поверхности ( кит. 指南针 , zhǐ nán zhēn — ложка, смотрящая на юг) использовался в династии Хань ( III век до н. э. ) для предсказаний . Согласно иной версии, первое упоминание магнита и магнитного компаса было сделано лишь в IV веке до н. э. в «Книге владельца Долины дьявола», а сам компас уже тогда выглядел как использовавшийся век спустя в фэншуе . Притяжение магнитом железа объяснялось с позиции проявления высших сил :
|
Яков Перельман в «Занимательной физике» отмечал, что китайское название магнита цы-ши ( кит. 磁石 ) переводится как «любящий камень» за притяжение железа, подобное отношениям между матерью и ребёнком . Однако подобные аналогии воздействия магнита на железо имеются и в других языках .
Плиний Старший в своём труде Naturalis Historia упоминал о горе возле реки Инд ( лат. Indus ), которая притягивала железо. Индийский врач Сушрута , живший в VI веке до н. э. , применял магниты в хирургических целях. Происхождение индийского компаса доподлинно неизвестно, но он упоминался уже в VI веке нашей эры в некоторых тамильских книгах по морской навигации под названием «рыбья машина» ( санскр. maccha-yantra ). В военном руководстве, датируемом 1044 годом был описан подобный компас в виде рыбы с головой из намагниченного железа, помещённой плавать в чашу.
Магнетит был хорошо известен древним грекам . Тит Лукреций Кар в своём сочинении « О природе вещей » ( лат. De rerum natura , I век до н. э. ) писал, что камень, притягивающий железо назывался в Греции магнитом по имени провинции Магнисия в Фессалии . По версии Плиния Старшего, слово «магнит» произошло от имени пастуха Магнеса
гвозди из обуви которого и наконечник его посоха были притянуты магнитным полем, когда он вывел на пастбище своё стадо.
Оригинальный текст (англ.)the nails of whose shoes and the tip of whose staff stuck fast in a magnetick field while he pastured his flocks.— Gilbert W. De Magnete / Gilbert Club, London, 1900. — transl., ed. — New York: Basic Books, 1958. — P. p.
Другое греческое название магнита — «Геркулесов камень» .
Первые греческие письменные упоминания магнетита относятся к VIII веку до н. э. Фалес Милетский ( VII — VI вв. до н. э. ) первым обратил внимание, что он притягивает железо . Различные философские школы объясняли его необычные свойства по-своему. Фалес и Анаксагор считали, что магнетит обладает душой , тянущейся к железу. Современник Анаксагора, Диоген из Аполлонии считал, что железо имеет некую «влажность» и магнит поглощает её. По иным теориям, магниты выделяли некоторые испарения, приводившие к наблюдавшимся результатам. Эмпедокл Акрагантский полагал, что магнитное взаимодействие имеет механическую природу, и для его проявления необходим прямой контакт между магнитом и железом. Эффект появления силы притяжения у железных колец, притянутых к магниту, был отмечен Сократом . Четыре века спустя, Лукреций Кар первым отметил, что магнитные материалы могут отталкиваться.
Во времена средневековья накопление новых знаний и теорий о природе магнетизма практически отсутствовало. Лишь монахами высказывались некоторые теологические предположения. Но в народном творчестве различных стран (не только европейских, но и арабских: см. « Тысяча и одна ночь ») иногда упоминались магнитные горы или острова, способные притягивать все металлические предметы вокруг.
Согласно одной из европейских легенд, магнитный компас изобрёл бедный ювелир Флавио Джойя, чтобы жениться на дочери богатого рыбака Доменико. Отец не желал себе такого зятя и поставил условие научиться плавать по прямой линии в тумане ночью. Находчивый ювелир заметил, что пробка с лежащим на ней магнитным камнем, помещённая в чашку с водой всегда ориентируется в одну сторону, и сумел выполнить сложное задание. В действительности же, «ювелиром» был папский секретарь Флавио Бьондо , в 1450 году описавший знание жителей Амальфи о компасе .
Впервые в Европе компас был упомянут в 1187 году англичанином Александром Неккамом в своих трудах De utensilibus и De naturis rerum .
Угол, на который отклоняется магнитная стрелка от направления север — юг, называют магнитным склонением . Христофор Колумб установил, что магнитное склонение зависит от географических координат, что послужило толчком к исследованию этого нового свойства магнитного поля Земли.
Одним из первых эксперименты с магнитами начал проводить иезуит Леонардо Гарцони еще в XVI в. Практически все накопленные к началу XVII века сведения о магнитах подытожили в 1589 году книгой «Естественная магия» Джамбаттиста делла Порта и в 1600 году Уильям Гильберт своим трудом « лат. De Magnete ». Магнитным силам эти учёные приписывали духовное происхождение. Русский учёный М. В. Ломоносов в 1759 г. в докладе «Рассуждение о большой точности морского пути» дал ценные советы, позволяющие увеличить точность показаний компаса. Для изучения земного магнетизма М. В. Ломоносов рекомендовал организовать сеть постоянных пунктов (обсерваторий), в которых производить систематические магнитные наблюдения; такие наблюдения необходимо широко проводить и на море. Мысль Ломоносова об организации магнитных обсерваторий была осуществлена лишь спустя 60 лет в России. Первую подробную материалистическую теорию магнетизма составил Р. Декарт . Теорию магнетизма разрабатывали также Ф. У. Т. Эпинус , Ш. Кулон , в 1788 году обобщивший закон Кулона на случай взаимодействия точечных полюсов магнита, , которому принадлежит открытие притяжения и отталкивания слабомагнитных веществ (названных М. Фарадеем в 1845 году диа- и парамагнетиками), и другие учёные.
Одной из важнейших вех в истории физики магнитных явлений стало осуществление в 1820 году опыта Эрстеда с магнитной стрелкой, фактически подтолкнувшего учёных к созданию единой теории электромагнитных взаимодействий. В том же году А. М. Ампер высказал гипотезу молекулярных токов, которая конкурировала с гипотезой элементарных магнитиков — магнитных диполей , детально разработанной В. Э. Вебером и развитой позднее Дж. А. Юингом . В 1831 г. английским полярным исследователем Джоном Россом в Канадском архипелаге был открыт магнитный полюс — область, где магнитная стрелка занимает вертикальное положение, то есть наклонение равно 90°. В 1841 г. Джеймс Росс (племянник Джона Росса) достиг другого магнитного полюса Земли, находящегося в Антарктиде.
В 1831 году М. Фарадей открыл закон электромагнитной индукции и впервые ввёл в обращение термин « магнитное поле ». В 1834 году русский академик Э. Х. Ленц установил правило о направлении индукционного тока и связанного с ним магнитного поля. В 1873 году начало современной электродинамике положило опубликование «Трактата об электричестве и магнетизме» Дж. К. Максвелла и экспериментальное обнаружение в 1888 году Г. Р. Герцем предсказанных в этом трактате электромагнитных волн . Взаимодействия электромагнитного поля с веществом рассматривал Х. А. Лоренц , создавший электронную теорию магнитных свойств и объяснивший в её рамках открытый в 1896 году эффект Зеемана .
В 1905 году П. Ланжевен на основе и развил классическую трактовку теории диа- и парамагнетизма.
Основной силовой характеристикой магнитного поля является вектор магнитной индукции . В среде вводится также вектор напряжённости магнитного поля .

В таблице ниже приведены размерности и единицы измерения магнитных величин, отнесённых к системе СИ . Колонка с обозначениями может содержать несколько вариантов, если они достаточно распространены в литературе. Используются следующие обозначения:
| Величина | Обозначение | Размерность | СИ | Гауссова СГС | СГСМ | СГСЭ |
|---|---|---|---|---|---|---|
| Магнитный дипольный момент | p , m , μ | IL 2 | 1 А · м 2 | 10 3 эрг / Гс | 10 3 · см 2 | 10 5 c Фр · см 2 |
| Индукция магнитного поля | B | MT −2 I −1 | 1 Тл | 10 4 Гс | 10 4 Гс | 100/c СГСЭ |
| Напряжённость магнитного поля | H | IL −1 | 1 А · м −1 | 4π⋅10 -3 Э | 4π⋅10 -3 Э | 4πc⋅10 -1 СГСЭ |
| Намагниченность | M , J | IL −1 | 1 А · м −1 | 10 −3 Э | 4π⋅10 -3 Э | 4πc⋅10 -1 СГСЭ |
| Магнитная восприимчивость | χ | 1 | 1 | 4π | 4π | 4π |
| Магнитная проницаемость (размерная, ) | μ | MLT −2 I −2 | 1 Гн · м −1 | 10 7 /4π Гс / Э | 10 7 /4π Гс / Э | 1000/4πc 2 СГСЭ |
| Магнитный поток | Φ | ML 2 T −2 I −1 | 1 Вб | 10 8 Мкс 2 | 10 8 Мкс | 1/10c СГСЭ |
| Векторный потенциал | A | MLT −2 I −1 | 1 Вб · м −1 | 10 6 Гс · см | 10 6 Мкс · см −1 | 1/c⋅10 4 СГСЭ |
| Индуктивность | L | ML 2 T −2 I −2 | 1 Гн | 10 9 | 10 9 | 10 5 /c 2 СГСЭ |
| Магнитодвижущая сила | F | I | 1 А | 4π⋅10 -3 | 4π⋅10 -3 | 4πc⋅10 9 СГСЭ |
Современная теория магнетизма базируется на следующих основных уравнениях и законах:
На микроскопическом уровне электромагнитные поля задаются (так называемые, микроскопические уравнения). Магнитное поле с микроскопической напряжённостью h описывается системой из двух уравнений ( СГС ):
где e — микроскопическая напряжённость электрического поля, а произведение плотности электрических зарядов на их скорость соответствует плотности тока. Микроскопические поля являются истинными, то есть возбуждаемыми движением элементарных зарядов в атомах , и оно сильно зависит от координат. Здесь ток ассоциируется с орбитальным и спиновым движением внутри атомов (молекулярные токи, концепцию которых предложил Ампер ). Переход к макроскопическим уравнениям происходит путём усреднения уравнений Лоренца — Максвелла. При этом среднюю напряжённость микроскопического магнитного поля называют магнитной индукцией :

Усреднённые по объёму молекулярные токи называют токами намагничивания. Когда внешнего поля нет, токи намагничивания в среднем равны нулю, а воздействие внешнего магнитного поля на вещество связано с их появлением. Если бы они были известны, то для вычисления полей было бы достаточно уравнений Максвелла для вакуума. Молекулярные токи можно интерпретировать как круговые токи, циркулирующие в атомах или молекулах вещества.
С каждым контуром молекулярного тока плотностью j m можно связать магнитный момент p . Это позволяет рассматривать ненамагниченное вещество как такое, где все магнитные моменты отдельных атомов направлены хаотически, а во внешнем магнитном поле они ориентируются определённым образом, тем самым вызывая изменение магнитного поля.
В действительности, верную интерпретацию магнетизма может дать только квантовомеханическое рассмотрение, так как существование элементарных магнитных диполей связано с квантованным орбитальным моментом и спином электронов, а не с классическими токами, которые быстро исчезли бы, например, в магнитных диэлектриках . Электрон со спином , может быть охарактеризован магнитным моментом с амплитудой
где g — множитель Ланде , а — магнетон Бора . На практике можно измерить лишь одну из трёх компонент вектора магнитного момента (например, проекцию на ось z ). Если S — суммарный спин орбитали изолированного атома, то проекция магнитного момента принимает значения
Атом с полным механическим моментом J обладает магнитным моментом с амплитудой
где множитель Ланде может быть сложной функцией от орбитальных квантовых чисел электронов атома . Упорядочивание спиновых и орбитальных моментов атомов позволяет наблюдать пара- и ферромагнетизм. Вклад в магнитные свойства веществ дают электроны частично заполненных атомных оболочек. Кроме того, в металлах может быть важным учёт электронов проводимости s-оболочек, магнитный момент которых является делокализированным.
Являясь квантовыми характеристиками, компоненты оператора спина не коммутируют друг с другом. Однако если ввести оператор среднего спина
где N — количество спинов в системе, то его компоненты будут коммутировать при :
где индексы α, β и γ пробегают по компонентам оператора среднего спина, i — мнимая единица , а — символ Леви-Чивиты . Это означает, что систему с достаточно большим количеством спинов можно рассматривать как классическую. Феноменологическое описание возможно применять к системам, где возбуждения имеют многочастичный характер (то есть, обменное взаимодействие должно существенно превышать релятивистские взаимодействия, такие как, например, ).
В теореме циркуляции магнитного поля необходимо учесть кроме токов проводимости j молекулярные токи j m ( индукция электрического поля для простоты считается нулевой):
|
|
|
|---|---|
|
|
|
где — магнитная постоянная .
Величину , характеризующую магнитный момент единицы объёма вещества, называют намагниченностью (иногда её обозначают буквой J ). Плотность молекулярных токов можно связать с намагниченностью просуммировав их по некоторой площади. Молекулярный ток равен циркуляции магнитного момента по контуру, охватывающему эту площадь. Тогда по теореме Стокса
|
|
|
|---|---|
|
|
|
Ротор намагниченности равен нулю, когда молекулярные токи в отдельных атомах или молекулах вещества ориентированны таким образом, что компенсируют друг друга.
Обычно вводят вспомогательное векторное поле
|
|
|
|---|---|
|
|
|
называемое напряжённостью магнитного поля . Тогда формула для циркуляции магнитного поля записывается как
|
|
|
|---|---|
|
|
|
В слабых полях намагниченность вещества пропорциональна напряжённости поля, что записывают как
где называют магнитной восприимчивостью . Это безразмерная величина, которая может изменяться в значительном диапазоне значений (к примеру, −2,6⋅10 −5 в серебре и около 2⋅10 5 в железе чистотой 99,95 % ) будучи как положительной, так и отрицательной. Связь между индукцией и напряжённостью магнитного поля можно записать как
|
|
|
|---|---|
|
|
|
где величину называют магнитной проницаемостью . В общем случае она является тензорной величиной.
Отличие между электрическими и магнитными свойствами кристаллов связано с различным поведением токов и зарядов по отношению к изменению знака времени. Обозначим через микроскопическую плотность зарядов в кристалле, а через — микроскопическую плотность токов в нём, усреднённые по времени. Преобразование временной координаты не меняет знака функции в отличие от функции . Но если состояние кристалла при этом не меняется, то должно выполняться условие , откуда следует, что . Кристаллы, для которых выполняется это условие не обладают магнитной структурой. Электрическая структура при этом существует всегда, так как нет причин, по которым плотность зарядов обращается в нуль при изменении знака времени. Магнитная структура является малым искажением по отношению к структуре немагнитной фазы и обычно возникает при понижении температуры, поскольку она связана со сравнительно слабыми взаимодействиями глубоко расположенных d- и f-электронов.
Удобней рассматривать симметрию не функции , а распределения намагниченности . Она соответствует симметрии расположения усреднённых по времени магнитных моментов в кристаллической решётке . Обозначим операцию преобразования направлений всех токов на противоположное символом R . Классы магнитной симметрии делятся на три типа. К первым двум относятся 32 обычных кристаллических класса и они же, дополненные операцией R . Третий тип составляют 58 классов, в которые R входит только с операциями поворота или отражения. Существует три типа пространственных магнитных групп, объединяющих 1651 группу. Первые два из них, как и в случае магнитных классов, содержат по 230 групп, совпадающих с кристаллографическими без операции R и дополненных ею. Третий класс содержит 1191 группу, в которой R комбинируется с поворотами , отражениями или трансляциями .
|
|
|
|---|---|
| C i (C 1 ) | C 3v (C 3 ) |
| C S (C 1 ) | D 3 (C 3 ) |
| C 2 (C 1 ) | D 3d (D 3 , S 6 , C 3v ) |
| C 2h (C i , C 2 , C S ) | C 3h (C 3 ) |
| C 2v (D 2 , C 2h , C 2v ) | C 6 (C 3 ) |
| D 2 (C 2 ) | D 3h (C 3h , C 3v , D 3 ) |
| D 2h (D 2 , C 2h , C 2v ) | C 6h (C 6 , S 6 , C 3h ) |
| C 4 (C 2 ) | C 6v (C 6 , C 3v ) |
| S 4 (C 2 ) | D 6 (C 6 , D 3 ) |
| D 2d (S 4 , D 2 , C 2v ) | D 6h (D 6 , C 6h , C 3v , D 3d , D 3h ) |
| D 4 (C 4 , D 2 ) | T h (T) |
| C 4v (C 4 , C 2v ) | O h (T) |
| C 4h (C 4 , C 2h , S 4 ) | T d (T) |
| D 4h (D 4 , C 4h , D 2h , C 4v , D 2h ) | O h (O, T h , T d ) |
| S 6 (C 3 ) | |
Магнитные кристаллического классы полностью определяют макроскопические магнитные свойства тела. Так спонтанная намагниченность кристалла будет присутствовать, если вектор намагниченности, являясь аксиальным вектором , не будет изменяться при преобразовании данного магнитного кристаллического класса.
Магнитными свойствами, выраженными в той или иной степени, обладают все вещества . Причиной взаимодействия со внешним магнитным полем являются собственные или наведённые магнитные моменты , которые ориентируясь определённым образом изменяют поле внутри вещества. Наиболее слабо магнитные эффекты проявляются в диа - и парамагнетиках . Атомы диамагнетиков не обладают собственным магнитным моментом и в соответствии с законом Ленца во внешнем поле внутри них появляются слабые круговые токи , стремящиеся компенсировать его. Атомы парамагнетиков обладают собственными слабыми магнитными моментами, которые при включении внешнего поля ориентируются вдоль него.
Существует несколько классов веществ, в которых взаимодействие между собственными магнитными моментами атомов особо сильное и имея квантовомеханическую природу принципиально не может быть объяснено с помощью аналогий классической физики . Магнитную структуру в них создаёт обменное взаимодействие. Вещества, в которых ближайшие магнитные моменты выстраиваются параллельно, называются ферромагнетиками . Антиферромагнетики и ферримагнетики обладают двумя ферромагнитными решётками с противоположными направлениями магнитных моментов, вложенными одна в другую. Различие между ними состоит в том, что решётки в антиферромагнетиках компенсируют друг друга, а в ферримагнетиках магнитные моменты различных решёток различны и суммарный магнитный момент не равен нулю. Говорят, что такие материалы (магнетики) имеют дальний магнитный порядок . Математическое описание магнитных подрешёток этих трёх классов веществ во многом подобно.


Также выделяют некоторые искусственные материалы, обладающие ближним магнитным порядком . Спиновые стёкла создаются добавлением магнитных примесей в немагнитные металлы и сплавы . Ансамбли ферро- или ферримагнитных частиц демонстрируют слабые парамагнитные свойства. В таком случае говорят о суперпарамагнетизме .
При описании ферро- и антиферромагнетиков часто применяют модель Гейзенберга . Она заключается в определении магнитной части гамильтониана кристалла в виде
| (ГейзГам) |
где индексы n и n' пробегают по узлам кристаллической решётки , а — оператор спина в n -м узле. Коэффициент называется , который обеспечивает магнитное упорядочивание изотропного кристалла. На практике полагают, что он существенно отличен от нуля лишь для ближайших соседей. Множитель ½ учитывает повтор при суммировании спинов по решётке (однако иногда его заносят в значение обменного интеграла). При данном выборе знака перед суммой ферромагнитному упорядочиванию соответствует положительное значение , а антиферромагнитному — отрицательное. Второе слагаемое является энергией взаимодействия системы спинов с магнитным полем ( Зеемановская энергия), магнитная индукция которого равна B (здесь g — множитель Ланде , — магнетон Бора ).
Гейзенберовский гамильтониан строится в предположении, что магнитные моменты (и спины, соответственно) локализированы в узлах кристаллической решётки, а орбитальные моменты отсутствуют. Первому условию отвечают ферромагнитные диэлектрики и полупроводники, но для металлов чаще бывает более предпочтительной зонная модель. Допустимость второго условия определяется степенью «замороженности» орбитальных моментов.
Построить микроскопическую модель антиферромагнетиков, аналогичную модели Гейзенберга невозможно, поэтому на макроскопическом уровне их представляют как совокупность нескольких магнитных подрешёток с противоположными направлениями намагниченности, вложенных одна в другую. Это описание хорошо соответствует экспериментальным данным.
Обменное взаимодействия проявляется вследствие кулоновского отталкивания электронов и принципа Паули . Оно является основной причиной, по которой проявляются ферромагнитные свойства веществ. Так как описывать обменное взаимодействие многоэлектронных систем с помощью микроскопического гамильтониана , учитывающего кинетическую энергию отдельных электронов, непрактично, обычно используют макроскопический гамильтониан, в котором операторы спинов заменяются квазиклассическими векторами спинов в форме Гейзенбергой модели (формула ), что является верным для спинов ½. Эмпирически обменный интеграл можно оценить как
где e — заряд электрона , a — постоянная магнитной решётки . Дать его точную теоретическую оценку очень сложно, поэтому на практике обычно используются экспериментально измеренные значения.
Обобщение, учитывающее обменную анизотропию (X—Y—Z модель) записывается в виде
где коэффициенты предполагаются слабо различающимися, так как само по себе обменное взаимодействие изотропно. Макроскопическая плотность энергии для ферромагнетиков, получаемая из Гейзенберовского гамильтониана записывается как
| (МакрОбм) |
где — координаты физического пространства, M — вектор намагниченности , константа обменного взаимодействия (в общем случае тензор )
а константа изотропного обмена
Здесь функцию полагают близкой к обменному интегралу при температурах, далёких от температуры Кюри . Константу A иногда называют константой анизотропного обмена для отличия от . Первое слагаемое в формуле является существенным при рассмотрении неоднородного распределения намагниченности, а второе — для изучения действия механизмов, изменяющих длину вектора намагниченности. Во многих случаях работает механизм не прямого обмена, связывающего спины соседних атомов через перекрытия их волновых функций и Кулоновскую энергию, а косвенного ( РККИ-обменное взаимодействие , суперобмен и др.).
Взаимодействия элементарных диполей между собою и с электрическим полем самой кристаллической решётки по своей природе являются релятивистскими . Отношение их энергий к энергии обменного взаимодействия по порядку величины равно , где v — скорость электрона в атоме, c — скорость света . Они приводят к установлению статистического равновесия и образованию избранных направлений намагниченности в кристаллах.
Под понимают взаимодействие элементарных магнитных диполей между собой. Оно уменьшается пропорционально кубу расстояния и доминирует над обменным взаимодействием на больших расстояниях, являясь причиной макроскопической намагниченности ферромагнетиков. К гамильтониану диполь-дипольного взаимодействия можно прийти, заменив классические диполи в формуле энергии взаимодействия двух магнитных моментов
на операторы , где — радиус-вектор , соединяющий точки расположения диполей, — магнетон Бора , — оператор полного орбитального момента , а — произведение Дираковского фактора Ланде и оператора полного спина атома в узле кристаллической решётки под номером n . Тогда гамильтониан дипольного взаимодействия примет вид
где суммирование производится по всем узлам магнитной подрешётки.
Переход к макроскопическому описанию даёт выражение для энергии в форме
Первое анизотропное слагаемое в подынтегральном выражении отражает вариации магнитного поля на расстояниях порядка атомных и зависит через тензор от структуры примитивной ячейки кристалла. Второе и третье слагаемые появляются как решение уравнений магнитостатики .
Взаимодействие спинов с электромагнитным полем кристаллической решётки или спин-орбитальное взаимодействие , а также приводят к появлению магнитной анизотропии. На макроскопическом уровне она наблюдается как энергетическая неэквивалентность различных направлений в кристалле, когда то или иное направление намагниченности по отношению к кристаллографическим осям оказывается более выгодным. В простейшем случае для одноосных ферромагнитных кристаллов, плотность энергии магнитной анизотропии может быть записана в двух эквивалентных формах через нормированный на единицу вектор намагниченности с проекциями , и (эквивалентность здесь означает точность до константы, не зависящей от направления намагниченности):
где коэффициент K называют константой анизотропии, а — угол между направлением вектора намагниченности и главной осью симметрии кристалла. В зависимости от знака K при данном выборе вида энергии говорят о легкоосных ( , намагниченность ориентируется вдоль оси для минимизации энергии: ) и легкоплоскостных магнетиках ( , намагниченность ориентируется перпендикулярно оси для минимизации энергии: ).
Кубические кристаллы существенно отличаются от одно- и двухосных по той причине, что их энергия анизотропии определяется членами четвёртого порядка в разложении по компонентам вектора намагниченности, нормированного на единицу:
Вследствие этого, их анизотропия выражена слабее. Для (например, у железа) минимум энергии достигается в направлениях рёбер куба [100] , [010] и [001], то есть существует три эквивалентные оси лёгкого намагничивания. Иначе осями лёгкого намагничивания будут пространственные диагонали куба.
![Ферромагнетик с одноосной анизотропией. Ось лёгкой намагниченности [001]](/images/004/958/4958866/85.jpg?rand=751492)
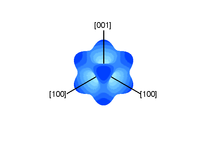


Понятие магнитного домена было введено Пьером Вейсом в 1907 году чтобы дать ответ на вопрос, почему железо будучи ферромагнетиком имеет нулевой магнитный момент при отсутствии внешнего поля. Под ферромагнитными доменами понимают макроскопические области магнитных кристаллов, в которых ориентация вектора спонтанной намагниченности различна. Они существуют при температуре ниже точки Кюри. Также говорят об антиферромагнитных доменах, подразумевая вектор антиферромагнетизма вместо намагниченности. Однако их существование, строго говоря, не приводит к выигрышу в энергии и обычно связывается с существованием нескольких зародышей антиферромагнитной структуры со случайным направлением намагниченности при переходе антиферромагнетика через точку Нееля .
Причина появления магнитных доменов в ферромагнетиках была предложена Львом Ландау и Евгением Лифшицем в 1937 году. Они предположили, что их образование приводит к минимизации полной энергии магнетика и поля рассеивания (то есть магнитного поля, создаваемого спонтанной намагниченностью и выходящего за пределы магнетика). Действительно, наблюдаемое на практике направление намагниченности в доменах в обычных условиях формирует замкнутый магнитный поток .

Граница между доменами имеет название доменной стенки . Её ширина определяется соотношением между обменной константой и константой анизотропии. В зависимости от результирующего угла поворота намагниченности различают 180°-е, 90°-е и другие доменные стенки. В зависимости от способа поворота намагниченности внутри 180°-х доменных стенок говорят о стенке Блоха и стенке Нееля . Последняя характерна для тонких магнитных плёнок, так как она обладает меньшим полем рассеяния, чем Блоховская стенка.
Существует много методов наблюдения доменов в ферромагнетиках. В 1932 году Фрэнсис Биттер предложил простой визуализации полей рассеивания с помощью коллоидных суспензий магнитных частиц, не требующий специального оборудования. Он заключается в том, что на поверхность магнетика наносятся магнитные микрочастицы, которые практически не испытывая трения концентрируются в местах наибольшего градиента поля, то есть на границах доменов. Их распределение можно наблюдать в оптический микроскоп. Применяются магнитооптические методы, основанные на повороте поляризации света. Для прозрачных плёнок это эффект Фарадея (изменение поляризации при прохождении сквозь образец), для иных — магнитооптический эффект Керра (изменение поляризации при отражении от образца). Преимуществом Керровской микроскопии является возможность прямого наблюдения доменов, это неразрушающий метод, однако при этом образцы должны быть плоскими, а для повышения контраста необходимо применять дополнительную обработку изображений. Кроме вышеописанных методик, используется ближнепольная микроскопия , рассеяние гамма-лучей и нейтронов , просвечивающая электронная микроскопия и др.
В диэлектриках и полупроводниках нет коллективизированных электронов в отличие от металлов . Следствием является локализация магнитных моментов вместе с электронами на ионных состояниях. Это является основным отличием магнетизма диэлектриков от магнетизма металлов, который описывается зонной теорией .
Согласно зонной теории, диэлектриками могут быть кристаллы, содержащие в примитивной ячейке чётное количество электронов. Это означает, что диэлектрики могут быть лишь диамагнетиками , что не объясняет свойств многих веществ. Причиной (парамагнетизм локализованных электронов), ферро - и антиферромагнетизма диэлектриков является кулоновское отталкивание электронов, что объясняется моделью Хаббарда на следующем примере. Появление дополнительного электрона в изолированном атоме увеличивает его энергию на некоторую величину . Следующий электрон попадёт на энергетический уровень , где — энергия кулоновского взаимодействия электронов, в реальных атомах колеблющаяся от 1 эВ до более чем 10 эВ. В кристалле энергетические уровни этих двух электронов расщепятся на зоны и кристалл будет диэлектриком или полупроводником, пока между ними существует запрещённая зона . Вместе обе зоны могут содержать чётное число электронов, но может быть ситуация, когда заполнена только нижняя зона и в ней находится нечётное число электронов. Диэлектрик, для которого выполняется это условие, называется диэлектриком Мотта — Хаббарда . Если интегралы перекрытия малы, диэлектрик будет парамагнетиком, иначе — антиферромагнетиком . За ферромагнетизм таких диэлектриков, как EuO или , отвечает суперобменное взаимодействие .

Большинство ферро- и ферримагнитных диэлектриков состоит из магнитных 3d- ионов , разделённых такими немагнитными ионами, как O 2− , Br − , Cl − и др. Образуется ситуация, когда расстояния для непосредственного взаимодействия 3d- орбиталей слишком велико и обменное взаимодействие осуществляется перекрытием волновых функций 3d-орбиталей магнитных ионов и p-орбиталей немагнитных ионов. Орбитали оказываются гибридизированными , а их электроны становятся общими для нескольких ионов. Такое взаимодействие называется суперобменным . Его знак (то есть, является ли диэлектрик ферро- или антиферромагнетиком) определяется типом d-орбиталей, количеством электронов на них и углом, под которым видна пара магнитных ионов из узла, где находится немагнитный ион.
Антисимметричное обменное взаимодействие (взаимодействие Дзялошинского — Мория) между двумя ячейками с векторами спина и описывается выражением
Очевидно, энергия взаимодействия ненулевая только если ячейки не магнитно эквивалентны. Взаимодействие Дзялошинского — Мория проявляется в некоторых антиферромагнетиках. Результатом является появление слабой спонтанной намагниченности . Этот эффект называют слабым ферромагнетизмом , так как результирующая намагниченность составляет десятые доли процентов от намагниченности в типичных ферромагнетиках. Слабый ферромагнетизм проявляется в гематите , карбонатах кобальта , марганца и некоторых других металлов.

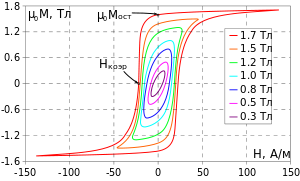
![Кобальт (спины направлены вверх[Комм 7])](/images/004/958/4958866/102.jpg?rand=521095)

Обменное взаимодействие в металлах может осуществляться принципиально различными механизмами, зависящим от типа атомных орбиталей , отвечающих за обменное взаимодействие. У таких переходных 3d-металлов как железо или кобальт , определяющую роль в обмене играет перекрытие 3d- волновых функций соседних атомов в кристаллической решётке, в то время, как у 4f-элементов обменное взаимодействие происходит посредством электронов проводимости . Манганиты лантана обладают сложной зависимостью магнитных свойств от степени их легирования .

3d-металлы характеризуются значительной энергией кулоновского взаимодействия между электронами 3d-зоны по сравнению с их кинетической энергией . Оно же фактически является причиной ферромагнитного упорядочивания. Как для 3d-, так и для 4f-элементов их магнитное упорядочивание зависит от степени заполнения соответствующей зоны. Переходной 3d-металл будет ферромагнетиком, если его 3d-зона содержит малое количество электронов или дырок (то есть она должна быть или слабо заполнена, или заполнена почти полностью). Это хорошо иллюстрируется железом, кобальтом и никелем , где эта зона почти полностью заполнена. Антиферромагнитное состояние будет основным, если она заполнена наполовину.
Условие, определяющее, будет ли металл ферро- или антиферромагнетиком, связано с тем, что электрону выгодно быть делокализованным, так как согласно принципу неопределённостей Гейзенберга , это позволяет уменьшить его кинетическую энергию. Качественно, его можно объяснить следующим образом. Для электронов должно соблюдаться правило Хунда (суммарный спин электронов на орбитали должен быть максимальным). Тогда для зоны, к примеру, заполненной меньше, чем наполовину, электроны двух соседних атомов могут иметь одинаковое направление спина, но разные магнитные квантовые числа , что и определяет ферромагнитное упорядочивание. В случае наполовину заполненной зоны, 3d-электроны соседних атомов вынуждены иметь противоположное направление суммарного спина для того, чтобы поделить между собой одинаковые магнитные числа.
Редкоземельные элементы имеют частично заполненную 4f- орбиталь , характерный размер которой существенно меньше межатомных расстояний в кристаллической решётке. Поэтому 4f-электроны соседних ионов не могут напрямую взаимодействовать друг с другом. Обменное взаимодействие между ними осуществляется с помощью электронов проводимости . Каждый редкоземельный ион создаёт возле себя достаточно сильное эффективное поле, которое поляризует электроны проводимости. Такое непрямое обменное взаимодействие между 4f-электронами называют взаимодействием Рудермана — Киттеля — Касуя — Иосиды (РККИ-обменное взаимодействие). Будет ли металл ферро- или антиферромагнетиком зависит от строения 4f-зоны и расстояния между ионами Зависимость обменного интеграла от произведения волнового вектора электронов на уровне Ферми k F и расстояния между магнитными ионами a имеет знакопеременный осциллирующий характер. Этим, в частности, объясняется существование геликоидальных и некоторых других магнитных структур. РККИ-взаимодействие существенно зависит от концентрации свободных носителей заряда и может быть существенно более дальнодействующим, чем прямой обмен .
Оксиды переходных металлов могут быть как проводниками, так и диэлектриками. В диэлектриках имеет место суперобменное взаимодействие. Однако управляя легированием можно добиться перехода оксида в проводящее состояние. В манганитах лантана вида La 1−x Ca x MnO 3 при определённых значениях параметра x про часть ионов марганца может иметь валентность 3+, а другая — 4+. Обменное взаимодействие между ними, совершаемое через ионы O 2- , называют двойным обменом . Эти соединения так же будут ферро- или антиферромагнетиками в зависимости от значения x . Ферромагнитное упорядочивание будет в том случае, если суммарные спины 3-х и 4-валентных ионов сонаправлены, при этом 4-й электрон может быть делокализован. Иначе он локализирован на ионе с меньшей валентностью. Для La 1−x Sr x MnO 3 переход из антиферромагнитной в ферромагнитную фазы происходит при (бо́льшим значениям x соответствует ферромагнетик).

Магнитное поле Земли служит для ориентации в пространстве многим видам животных. По не выясненным до конца причинам, птицы и черепахи используют информацию о магнитном наклонении , а лососёвые, и рукокрылые реагируют на горизонтальную компоненту поля. «Компас» птиц в нормальном режиме функционирует в интервале полей от 43 до 56 мкТ , но после адаптации способен воспринимать поля от 16 до 150 мкТ. При этом птицы не различают северный и южный магнитные полюса и нуждаются в дополнительной световой информации для ориентирования. Чувствительными к магнитному полю также являются морские моллюски, саламандры (например, Eurycea lucifuga ), тритоны (например, зеленоватый тритон ), шершни, медоносные пчёлы и аллигаторы . Морские черепахи и некоторые виды беспозвоночных, наряду с птицами, также обладают способностью составлять «магнитные карты», помогающие им находить дорогу .
Существуют различные рецепторы , реагирующие на внешнее магнитное поле. В глазах дрозофил и некоторых птиц содержатся молекулы криптохрома , некоторые другие (например, ( англ. )) содержат в своём теле однодоменные частицы. Некоторые бактерии используют специальные органеллы — магнетосомы . В то же время, многие животные способны определять поляризацию солнечного света и ориентироваться по звёздам. Поэтому, несмотря на доказанное умение многих видов применять магнитные поля для определения направления, однозначного ответа на вопрос, как именно ориентируется в пространстве то или иное животное находясь в дикой природе, на данное время нет.
Эффективность воздействия электромагнитных полей на живые организмы связана с наличием «окон чувствительности» по амплитуде, градиенту и частоте, иногда специфическое воздействие может оказать последовательность сигналов определённой формы. Внутренний компас животных может быть связан с наличием в организме частиц магнетита , например, в форме ферритина . Магнетит также встречается в мозге человека, и в ещё большей концентрации в мозге птиц. Человеческий мозг содержит около 5 миллионов кристаллов на грамм, а в его мембранах содержится около 100 миллионов кристаллов на грамм. Отклик магнетита на магнитное поле более чем в миллион раз превышает отклик обычной пара- или диамагнитной среды и, предположительно, это может оказывать влияние на транспорт ионов между клетками. Чувствительность шишковидного тела в мозге млекопитающих к магнитным полям связана с функционированием сетчатки глаза. Это приводит к тому, что сетчатка включается в магниторецептивную систему организма. Её роль иллюстрируется тем фактом, что при ослаблении градиента магнитного поля Земли до 30 нТ/м, у большинства людей снижается ( англ. ).
Существует несколько видов анаэробных бактерий ( ( англ. ): и др.), способных реагировать на внешние магнитные поля. Они содержат органелы, называемые магнетосомами , в мембранах которых содержатся однодоменные кристаллы магнетита Fe 3 O 4 или Fe 3 S 4 (иногда и те, и другие вместе). Размер кристаллов колеблется в пределах от 40 до 100 нм. Магнетосомы образуют цепочки, закреплённые внутри бактерии таким образом, что направление намагниченности магнитных нанокристаллов совпадает с направлением цепочек .
Магнетотактические бактерии являются природными компасами , которые ориентируются вдоль направления магнитного поля Земли . Благодаря тому, что они реагируют на слабые поля напряжённостью порядка 0,5 эрстед, они используются в скоростных высокочувствительных методах визуализации доменной структуры магнетиков (например, для проверки трансформаторной стали ). При помещении магнетотактических бактерий на магнитную поверхность они за несколько секунд перемещаются вдоль силовых линий к северным полюсам скапливаясь в местах, где магнитное поле перпендикулярно поверхности. Методы с применением магнетотактических бактерий дают лучший контраст чем классический или . Естественным ограничением их разрешения служит размер бактерии порядка одного микрометра.