Скачка идей
- 1 year ago
- 0
- 0
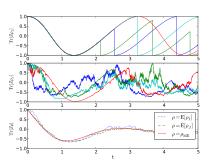
????? ?????????? ?????? , ????? ????????? ??? ???????? ??????? ?????-????? (MCWF) , – ????? ?????????????? ?????? , ???????????? ??? ????????????? ???????? ????????? ?????? ? ????????? ?????????? . ????? ?????????? ?????? ??? ?????????? ?????????? , ???????? ? ???????? ???????????? ? ??????????? ???????, ????????? ??? ?????? ????????? ??????????, ????????????? ?????????? . ?????? ????????????? ?????? ?? ???????? ?????-????? ? ???????? ????????? ????????, ?????????? ?? ???????? ????????, ???????? ?????? ????, ??????? ? ?????, ? ????? ???????????? ? ????????.
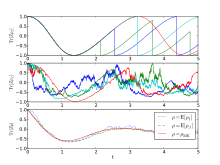
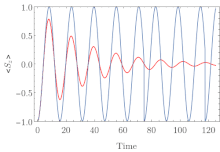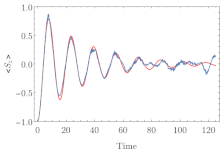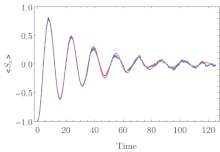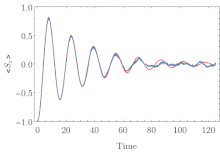
????? ?????????? ?????? — ??? ??????, ??????? ?? ?????? ????? ?? ?????? ? ?????????????? ????????? ????????? , ?? ??????????? ????, ??? ?? ???????? ? ???????? ????????, ? ?? ? ?????????????? ??????? ? ???????? ????????? . ???????? ??????????? ????? ?????? ???????? ???????? ???????? ??????? ??????? ?? ??????? ? ??????? ???????????????????; ??? ?? ?????? ????????? ???? ? ????????? ???????????? ????? ????????? ????????? ?????? (??????????? ?????????). ???????????? ????????? ??????? ??? ??????? ??????? ???????? ??? ????????? ??????????, ? ???????? ??????? ????????? ??? ??????? ??????? ????? ???? ?????????? ????? ?????????? ?? ????????? ??????????????? ??????????. ??? ??????????? ???????????? ??????????? N ????? ????????? ???????? ??????? ????? N, ? ?????????? ????????? ??????? ????????? ????? N 2 . ?????????????, ??? ????????? ????? ????? ?????????? ?????? ???? ???????????? ? ?????????????????? ?? ????????? ? ????????? ? ?????????????? ??????? ????????? ?????????.