16 кварталов
- 1 year ago
- 0
- 0

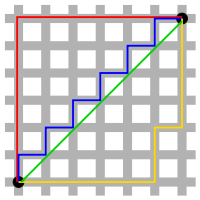
Расстояние городских кварталов — метрика , введённая Германом Минковским . Согласно этой метрике, расстояние между двумя точками равно сумме модулей разностей их координат.
У этой метрики много имён. Расстояние городских кварталов также известно как манхэттенское расстояние , метрика прямоугольного города , метрика L1 или норма (см. пространство L p ), метрика городского квартала , метрика такси , метрика Манхэттена , прямоугольная метрика , метрика прямого угла ; на её называют метрикой гриды и 4-метрикой .
Название «манхэттенское расстояние» связано с уличной планировкой Манхэттена .
Расстояние городских кварталов между двумя векторами в n -мерном вещественном векторном пространстве с заданной системой координат — сумма длин проекций отрезка между точками на оси координат. Более формально,
где
Например, на плоскости расстояние городских кварталов между и равно
Манхэттенское расстояние зависит от вращения системы координат, но не зависит от отражения относительно оси координат или переноса . В геометрии, основанной на манхэттенском расстоянии, выполняются все аксиомы Гильберта , кроме аксиомы о конгруэнтных треугольниках.
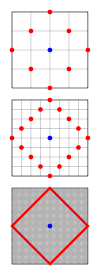
Для трёхмерного пространства, шар в этой метрике имеет форму октаэдра , вершины которого лежат на осях координат.
| a | b | c | d | e | f | g | h | ||
|---|---|---|---|---|---|---|---|---|---|
| 8 |

|
8 | |||||||
| 7 | 7 | ||||||||
| 6 | 6 | ||||||||
| 5 | 5 | ||||||||
| 4 | 4 | ||||||||
| 3 | 3 | ||||||||
| 2 | 2 | ||||||||
| 1 | 1 | ||||||||
| a | b | c | d | e | f | g | h | ||
Расстояние между полями шахматной доски для визиря (или ладьи , если расстояние считать в полях) равно манхэттенскому расстоянию; король пользуется расстоянием Чебышёва , а слон — манхэттенским расстоянием на доске, повёрнутой на 45°.
Сумма манхэттенских расстояний между костяшками и позициями, в которых они находятся в решённой головоломке « Пятнашки », используется в качестве эвристической функции для поиска оптимального решения .
Множество клеток на двумерном квадратном паркете , манхэттенское расстояние до которых от данной клетки не превышает r , называется окрестностью фон Неймана диапазона (радиуса) r .