Призма , оптическая призма — тело из однородного материала, прозрачного для оптического излучения , ограниченное плоскими отражающими и преломляющими свет поверхностями, расположенными под строго определёнными углами друг к другу . Для призм, использующихся в оптических приборах , используется оптическое стекло с разными показателями преломления , зависящими от типа и назначения призмы. Оптические призмы подразделяют на три крупных и чётко различающихся по назначению класса: спектральные призмы (преломляющие, или дисперсионные призмы для разложения света в спектр ), отражательные призмы (для изменения направления света) и поляризационные призмы (для получения линейно поляризованного света). Изготавливаются главным образом из стекла , кварца , флюорита , фторида лития , бромида калия и других веществ .

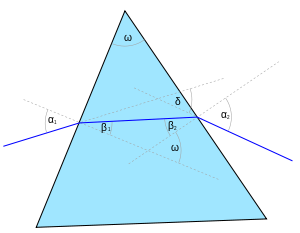
Путь лучей в треугольной призме

Простейшим типом призмы является треугольная призма, то есть тело, представляющее собой геометрическую фигуру призма с двумя треугольными основаниями и тремя боковыми гранями в форме прямоугольников .

На рисунке показано сечение треугольной призмы плоскостью, параллельной её основаниям. Обозначения: ${\displaystyle \delta }$ — угол отклонения, ${\displaystyle \omega }$ — преломляющий угол призмы, ${\displaystyle \alpha _{1},\beta _{2}}$ — углы падения, соответственно, входящего через боковую грань призмы луча и луча, выходящего через другую её боковую грань, ${\displaystyle \beta _{1},\alpha _{2}}$ — углы преломления этих двух лучей соответственно. На данном рисунке материал призмы — оптически более плотная среда, чем её окружение, поскольку угол падения входящего луча больше его угла преломления. То есть относительный показатель преломления этого материала — больше единицы, обозначим его ${\displaystyle n}$ . Самая простая формула для угла отклонения получается, если предположить, что преломляющий угол призмы и угол падения входящего луча малы . Тогда будет мал и угол ${\displaystyle \alpha _{2}}$ , а значит, малы будут и углы ${\displaystyle \beta _{1},\beta _{2}}$ . По закону преломления света :

${\displaystyle \alpha _{1}\approx \sin \alpha _{1}=n\cdot \sin \beta _{1}\approx n\cdot \beta _{1},}$

${\displaystyle \alpha _{2}\approx \sin \alpha _{2}=n\cdot \sin \beta _{2}\approx n\cdot \beta _{2}}$

Учитывая, что сумма углов четырёхугольника равна ${\displaystyle 2\pi }$ и принимая во внимание, что ${\displaystyle \omega =\beta _{1}+\beta _{2}}$ :

${\displaystyle \pi -\delta +\pi -\omega +\alpha _{1}+\alpha _{2}=2\pi ,}$

${\displaystyle \delta =\alpha _{1}+\alpha _{2}-\omega \approx n\cdot (\beta _{1}+\beta _{2})-\omega =n\cdot \omega -\omega =(n-1)\cdot \omega }$

Таким образом, при малом угле падения входящего луча имеем приближённую формулу для угла отклонения:

${\displaystyle \delta \approx (n-1)\cdot \omega }$

Эта формула важна ещё и потому, что с её помощью можно вывести зависимость фокусного расстояния тонкой линзы от радиусов её поверхностей, при этом тонкая линза заменяется треугольной призмой и применяется формула для угла отклонения .

В случае произвольных преломляющего угла призмы и угла падения входящего луча, и если абсолютный показатель преломления материала призмы равен ${\displaystyle n_{2}}$ , а её окружения — ${\displaystyle n_{1}}$ , подобными рассуждениями можно получить формулу :

${\displaystyle \delta =\alpha _{1}-\omega +\arcsin {\bigg (}{\frac {n_{2}}{n_{1}}}\cdot \sin \omega \cdot {\sqrt {1-{\bigg (}{\frac {n_{1}}{n_{2}}}{\bigg )}^{2}\cdot \sin ^{2}\alpha _{1}}}-\cos \omega \cdot \sin \alpha _{1}{\bigg )}}$

Виды призм

Дисперсионные призмы

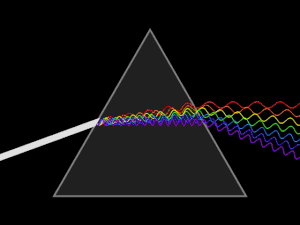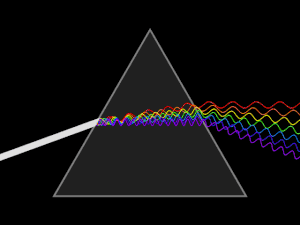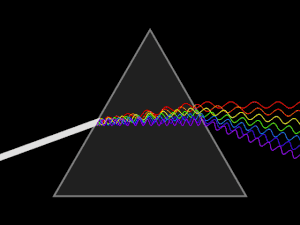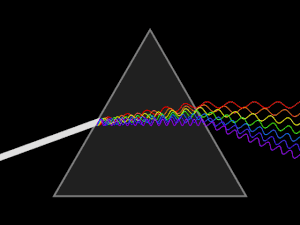
Дисперсионные призмы используют в спектральных приборах для пространственного разделения излучений различных длин волн.

• Простая трёхгранная призма — призма с преломляющим углом ${\displaystyle \omega }$ = 60°.
• — призма, состоящая из двух одинаковых вспомогательных призм с небольшим преломляющим углом, изготовленных из крона, и одной основной призмы из флинта.
• Призма Аббе — один из типов дисперсионных призм постоянного отклонения, в основе которых находится треугольник с углами 30°, 60° и 90°.
• Призма Амичи — преломляющая призма, склеенная из трёх треугольных призм, две крайние из которых изготавливаются из стекла кронгласс с большой дисперсией, а средняя из стекла флинтглас с малой дисперсией.
• — призмы с преломляющим углом 30°, заднюю поверхность которой покрывают отражающим слоем серебра, так что лучи пересекают призму дважды в противоположных направлениях.
• — призма, представляющая собой соединение на оптическом контакте двух прямоугольных призм, вырезанных из лево- и правовращающего кварца.
• Призма Пеллин — Брока — разновидность дисперсионной призмы, состоящая из четырёхстороннего блока стекла в виде правой призмы с углами 90°, 75°, 135° и 60° на торцах.

Отражательные призмы

Отражательные призмы используют для изменения хода лучей, изменения направления оптической оси, изменения направления линии визирования, для уменьшения габаритных размеров приборов. Классифицируются отражательные призмы по нескольким признакам:

• количеству отражений в призме
• наличию или отсутствию «крыши»
• характеру конструкции призмы
• углу излома оптической оси

Также, особую нишу среди отражательных призм занимают составные призмы, — состоящие из нескольких частей, разделённых воздушными промежутками. Некоторые широко распространённые призмы получили собственные имена.

• Призма Аббе
• Призма Аббе — Порро
• Призма Аббе — Кёнига
• Призма Дове
• Пентапризма
• Призма Порро

Название призмы обозначается двумя или тремя буквами и числом, записанным через дефис. Первая буква означает количество отражательных граней (отражений) в призме («А» — одна, «Б» — две, «В» — три и т. д.). «Крыша», условно, считается одной гранью и для её обозначения ставят индекс «к» после первой буквы (например, Ак, Бк). Оставшаяся буква указывает характер конструкции («Р» — равнобедренная, «П» — пентапризма, «У» — полупентапризма, «С» — ромбическая, «М» — дальномерного типа, «Л» — призма Лемана). Цифры, записанные через дефис, указывают угол излома оптической оси (0°, 90°,180°). Например, «ВкР-45°» — равнобедренная призма с тремя отражательными гранями и крышей, с изломом оси на 45°.

Составные призмы указываются по их собственным именам и углам излома оси. Например, «А-0°» — Призма Аббе, «Бк-90°» — башмачная призма с крышей, «К-0°» — призма-куб.

Поляризационные призмы

• Призма Волластона
• Призма Глана — Тейлора
• Призма Глана — Томпсона
• Призма Глана — Фуко
• Призма Николя
• Призма Номарски
• Призма Сенармона
• Параллелепипед Френеля

Отклоняющие призмы

используются для отклонения луча света на фиксированный угол. Пара таких призм может использоваться для : вращая призмы, луч можно отклонить на любой желаемый угол в коническом «поле обзора». Чаще всего встречается пара . Две клиновые призмы также могут использоваться в качестве анаморфной пары для изменения формы сечения луча. Это используется для получения круглого луча из эллиптического на выходе лазерного диода .

Ромбовидные призмы используются для бокового смещения луча света без инвертирования изображения.

использовались на парусных судах для обеспечения дневного света под палубой поскольку свечи и керосиновые лампы могут быть пожароопасны на деревянных кораблях.

История

Как и многие основные геометрические термины, слово призма имеет греческое происхождение ( греч. πρίσμα ). Термин впервые был использован в « Началах » Евклида. Евклид определил термин в книге XI как «твёрдую фигуру, ограниченную двумя противоположными, равными и параллельными плоскостями, в то время как остальные представляют собой параллелограммы», однако девять последующих утверждений, в которых использовался этот термин, включали примеры призм с треугольным основанием (то есть со сторонами, которые не были параллелограммами) . Это несоответствие вызывало замешательство у более поздних геометров .

Рене Декарт видел свет, разделённый на цвета радуги стеклом или водой , хотя происхождение цвета было неизвестно. Эксперимент Исаака Ньютона в 1666 году по пропусканию белого света через призму продемонстрировал, что все цвета уже существуют в свете, с разноцветными « корпускулами », расходящимися веером и перемещающимися с разной скоростью через призму. Только позже Янг и Френель объединили теорию частиц Ньютона с волновой теорией Гюйгенса , чтобы объяснить, как цвет возникает из светового спектра.

Ньютон пришёл к своему выводу, пропустив красный цвет из одной призмы через вторую, и обнаружил, что цвет не изменился. Из этого он пришел к выводу, что цвета уже должны присутствовать в падающем свете — таким образом, призма не создавала цвета, а просто разделяла цвета, которые уже есть. Он также использовал линзу и вторую призму, чтобы преобразовать спектр обратно в белый свет. Этот эксперимент стал классическим примером методологии, введенной во время научной революции .

Ньютон подробно рассмотрел дисперсию света в призме в своей книге « Оптика» . Он также ввёл использование более чем одной призмы для управления дисперсией . Описание Ньютоном своих экспериментов по рассеиванию света призмами было качественным. Количественное описание не требовалось до тех пор, пока в 1980-х годах не были введены .

См. также

• Гризма
• Призма (геометрия)
• Оптическое явление

Примечания

Литература

• Е. А. Иофис . / И. Ю. Шебалин. — М.,: «Советская энциклопедия», 1981. — С. —253. — 447 с.

• Hecht, Eugene. Optics (4th ed.) (неопр.) . — (англ.) ( , 2001.

Ссылки

• (недоступная ссылка с 12-03-2018 [2136 дней])