Interested Article - Симметрия (физика)

- 2020-05-13
- 1
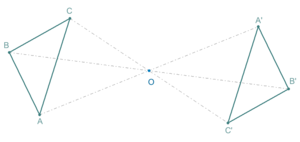
Симме́три́я в широком смысле — соответствие, неизменность ( инвариантность ), проявляемые при каких-либо изменениях, преобразованиях (например: положения , энергии , информации , другого). В физике , симметрия физической системы — это некоторое свойство, сохраняющееся после проведения преобразований .
Симме́три́я ( симметрии ) — одно из фундаментальных понятий в современной физике , играющее важнейшую роль в формулировке современных физических теорий . Симметрии, учитываемые в физике, довольно разнообразны, начиная с симметрий обычного трёхмерного «физического пространства» (такими, например, как зеркальная симметрия), продолжая более абстрактными и менее наглядными (такими как калибровочная инвариантность ).
Некоторые симметрии в современной физике считаются точными, другие — лишь приближёнными. Также важную роль играет концепция спонтанного нарушения симметрии .
Исторически использование симметрии в физике прослеживается с древности, но наиболее революционным для физики в целом, по-видимому, стало применение такого принципа симметрии, как принцип относительности (как у Галилея , так и у Пуанкаре — Лоренца — Эйнштейна ), ставшего затем как бы образцом для введения и использования в теоретической физике других принципов симметрии (первым из которых стал, по-видимому, принцип общей ковариантности , являющимся достаточно прямым расширением принципа относительности и приведшего к общей теории относительности Эйнштейна ).
Группой симметрии физической задачи называется группа, каждый элемент которой является линейной операцией симметрии задачи, отображающий один элемент множества решений задачи, в другой.
Исходя из принципов симметрии, можно выводить новые законы природы дедуктивно, а не только в результате наблюдения над физическими объектами или в результате решения уравнений .
Теорема Нётер
В 1918 году немецкий математик Эмми Нётер доказала теорему, согласно которой каждой непрерывной симметрии физической системы соответствует некоторый закон сохранения . Наличие этой теоремы позволяет проводить анализ физической системы на основе имеющихся данных о симметрии, которой эта система обладает. Из неё, например, следует, что инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии ; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса ; инвариантность относительно вращений — к закону сохранения момента импульса .
См. также
Примечания
- , с. 56.
- А. М. Балдин от 24 января 2022 на Wayback Machine // Краткие сообщения ОИЯИ. — 1(93) 1999, c. 5 — 13
Литература
- Ферми Э. Квантовая механика. — М. : Мир, 1968. — 366 с.
- Любарский Г. Я. Теория групп и физика. — М. : Наука, 1986. — 224 с.
|
Для улучшения этой статьи по физике
желательно
:
|
- 2020-05-13
- 1